実験3：円生成アルゴリズム
3.1実験目的
（1）DDAアルゴリズム、中点円法、ブレゼンハムアルゴリズムを理解する
（2）VC++でのCDCクラスの使用法を習得する
3.2実験内容
（1）クラスライティング
（2）完全なDDAアルゴリズム、中点円法、ブレゼンハムアルゴリズム
3.3アルゴリズムのアイデア
平面解析幾何学では、円の方程式は（x–x0）2+（y–y0）2 = R2として記述できます。ここで、（x0、y0）は中心座標であり、Rは円の半径です。特に、（x0、y0）が座標の中心点である場合、円の方程式はx2 + y2=R2に簡略化できます。コンピュータグラフィックスでは、直線のような円にもドットマトリックス出力デバイスでの表示または出力の問題があるため、一連のラスタースキャン変換アルゴリズムも必要です。簡単にするために、まず中心が原点にある円の生成を考えます。中心が原点にない円の場合、対応する位置の円は座標の平行移動変換によって取得できます。
スキャン変換の前に、円の特性、つまり円の八分儀を理解する必要があります。次の図に示すように、
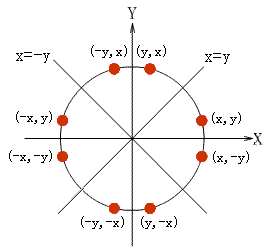中心が原点にある円には、4つの対称軸x = 0、y = 0、x = y、x = -yがあります。円弧上の点P（x、y）がわかっている場合、4つの対称軸の7つの対称点にすることができます：（x、-y）、（-x、y）、（-x、-y）、（y、x）、（y、-x）、（-y 、x）、（-y、-x）、このプロパティはオクタント対称と呼ばれます。したがって、円弧の8分の1を描くことができる限り、対称性の原理を使用して円全体を得ることができます。
円のスキャン変換を取得する簡単な方法がいくつかあります。まず、デカルト座標法です。既知の円方程式：x2 + y2 = R2、xを独立変数とすると、yを解きます。
円を生成するときは、最初に円周の1/4をスキャンして変換し、独立変数xを単位ステップで0からRに増やし、各ステップでyを解いてから、ポイント関数を呼び出して円を1点ずつ描画します。ただし、そうする場合、累乗演算と平方根演算があり、どちらも浮動小数点演算であるため、アルゴリズムは効率的ではありません。また、xがRの値に近い場合（円の中心が原点にある場合）、円周上の点（R、0）の近くでは、円の傾きが無限大になる傾向があるため、浮動小数点数は次のようになります。円周に大きな円ができるように切り上げます。ギャップ。次に、極座標法を紹介します。デカルト座標系の円弧上の点P（x、y）とx軸の間の角度をθとすると、円の極座標方程式は次のようになります
。 Rcosθy
=Rsinθ
円は、を使用して生成されます。円の8番目の対称性により、独立変数θの値の範囲が（0、45°）の場合、完全な円を描くことができます。
（1）角度数値微分法（DDA法）：
直交座標系の円のパラメトリック方程式は次のとおりです。
{█（x =x0+Rcosθ@y= y0 +Rsinθ）┤
上記の式から導出
x-xc = -Rsinθdθy -
yc=Rcosθdθx
-xcを-rからrに1ずつ増やすと、対応する円点のy座標を取得できます。ただし、このようにして得られた円上の点は均一ではなく、| x-xc |が大きいほど、対応する円点間の円距離は長くなります。したがって、結果として得られる円は見た目に美しいものではありません。
（2）中点で円を描く方法：
原点で円の中心を考えます。Rの半径は、点（0、R）から点（0、R）まで時計回りに第1象限の8番目の円弧です。 R /、R /）。この円弧を決定します。次の図に示すように、点Pi（xi、yi）がすでに実際の円弧に最も近い円弧上の点であるとすると、Piの次の点は右のP1または右下のP2のいずれかになります。 ：
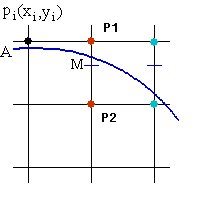判別関数を作成します
。F（x、y）= x2 + y2–R2
F（x、y）= 0の場合、点は円上にあり、F（x、y）> 0の場合、 F（x、y）<0の場合、ポイントは円の外側にあります。これは、ポイントが円の内側にあることを意味します。MがP1とP2の中点である場合、Mの座標は（xi + 1、yi–0.5）であり、F（xi + 1、yi–0.5）<0の場合、点Mは円の内側にあり、その点を示します。 P1は遠くにあります実際の円弧はより近く、円の次の点としてP1を取る必要があります。同様に、F（xi + 1、yi–0.5）> 0の場合、P2は実際の円弧に近く、P2を次の点と見なす必要があります。F（xi + 1、yi–0.5）= 0の場合、P1とP2の両方を円の次の点として使用でき、アルゴリズムはP2を次の点として使用することに同意します。
（3）ブレゼンハムの円描画アルゴリズム：
判別式を整数演算に還元できれば、計算を簡略化して効率を上げることができます。そのため、人々は中点円法にさまざまな改良を加えました。その1つは、円の半径Rが常に2より大きいことを考慮して、dの初期値を1.25–Rから1–Rに変更することです。浮動小数点演算を回避しながら、dの初期値の符号に影響を与えません。もう1つの方法は、dの計算を2倍にして、初期値を3–2Rに変更することです。これにより、浮動小数点演算が回避されます。また、改善の初期値として3–2Rを使用して、シフトによって2の乗算をすばやく置き換えることもできます。ブレゼンハムのアルゴリズムとしても知られるアルゴリズム。
3.4フローチャート
（1）角度数値微分法（DDA法）:(
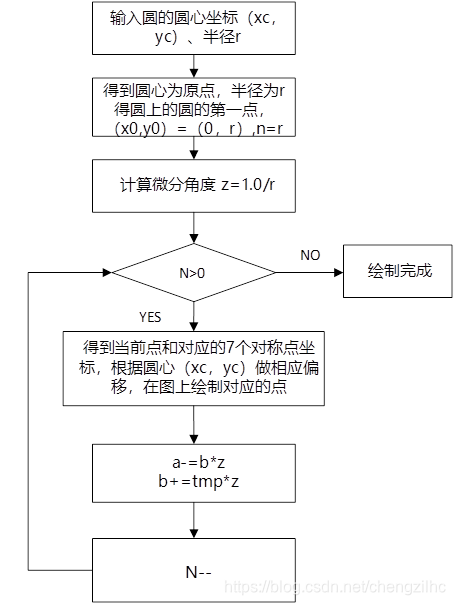2）中点円描画法：
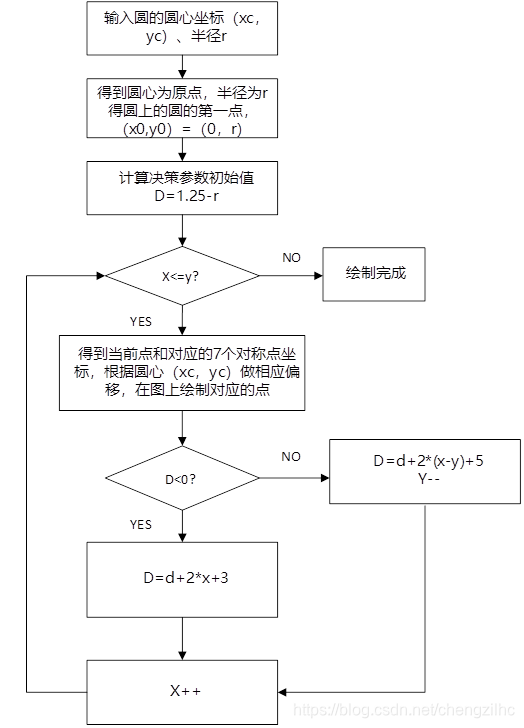（3）ブレゼンハム描画円アルゴリズム：
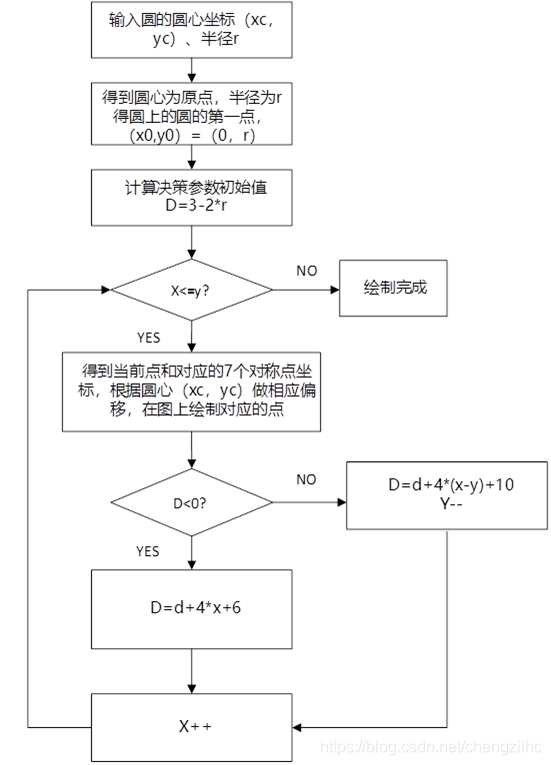
3.5実験手順
（1）角度数値判別法（DDA法）：
長方形座標系の円のパラメトリック方程式は次のとおりです。
{█（x =x0+Rcosθ@y= y0 +Rsinθ）┤
上記の式から導出
x-xc = -Rsinθdθy-
yc=Rcosθdθ
導関数：
xn + 1 = xn-（yn-y0）
dθyn+ 1 = yn-（xn-x0）dθ
（2）中点円法：
1）判別関数を作成します：F（x 、y）= x2 + y2–R2。
F（x、y）= 0の場合、ポイントは円上にあり、F（x、y）> 0の場合、ポイントは円の外側にあり、F（x、y）<0の場合、ポイントが円の内側にあることを意味します。
MがP1とP2の中点である場合、Mの座標は（xi + 1、yi–0.5）であり、F（xi + 1、yi–0.5）<0の場合、点Mは円の内側にあり、その点を示します。 P1は遠くにあります実際の円弧はより近く、円の次の点としてP1を取る必要があります。
同様に、F（xi + 1、yi–0.5）> 0の場合、P2は実際の円弧に近く、P2を次の点と見なす必要があります。F（xi + 1、yi–0.5）= 0の場合、P1とP2の両方を円の次の点として使用でき、アルゴリズムはP2を次の点として使用することに同意します。
2）M点（xi + 1、yi–0.5）の座標を判別関数F（x、y）に入れて、判別式dを取得します
。d= F（xi + 1、yi–0.5）=（xi + 1 ）2 +（yi–0.5）2–R2
3）d <0の場合、P1を次の点とし、P1の次の点の判別式は次のようになります
。d'= F（xi + 2、yi–0.5） =（xi + 2）2+（yi–0.5）2–R2
が展開され、dが判別式の漸化式になります：
d'= d + 2xi + 3
d> 0の場合、P2を次の点とし、P2の次の点の判別式は次のようになります
。d'= F（xi + 2、yi–1.5）=（xi + 2）2+（yi–1.5） 2–R2
が展開され、dが漸化式になり、判別式が得られます
。d'= d + 2（xi-yi）+5
4）特に、第1象限（0、R）の最初の点で、判別式dの初期値d0は、次のように推定できます
。d0 = F（1、R–0.5）= 1–（R–0.5）2–R2 = 1.25-R
円の中心が原点にないことを考慮すると、計算された座標が変換されるのを修正する必要があります。
（3）ブレゼンハムの円描画アルゴリズム：
1）判別関数F（x、y）= x2+y2-R2を作成します。
F（x、y）= 0の場合、ポイントは円上にあり、F（x、y）> 0の場合、ポイントは円の外側にあり、F（x、y）<0の場合、ポイントが円の内側にあることを意味します。
MがP1とP2の中点である場合、Mの座標は（xi + 1、yi–0.5）であり、F（xi + 1、yi–0.5）<0の場合、点Mは円の内側にあり、その点を示します。 P1は遠くにあります実際の円弧はより近く、円の次の点としてP1を取る必要があります。
同様に、F（xi + 1、yi–0.5）> 0の場合、P2は実際の円弧に近く、P2を次の点と見なす必要があります。F（xi + 1、yi–0.5）= 0の場合、P1とP2の両方を円の次の点として使用でき、アルゴリズムはP2を次の点として使用することに同意します。
2）M点（xi + 1、yi–0.5）の座標を判別関数F（x、y）に入れて、判別式dを取得します
。d= F（xi + 1、yi–0.5）=（xi + 1 ）2 +（yi–0.5）2–R2
3）d <0の場合、P1を次の点とし、P1の次の点の判別式は次のようになります
。d'= F（xi + 2、yi–0.5） =（xi + 2）2+（yi–0.5）2–R2
展開後、dを判別式の漸化式に入れます
。d'= d + 4xi + 6
d> 0の場合、P2を次の点とし、P2の次の点の判別式は次のようになります
。d'= F（ xi + 2、yi–1.5）=（xi + 2）2+（yi–1.5）2–R2
展開後、dを漸化式にして、判別式を取得します
。d'= d + 4（xi -yi）+ 10
4）特に、第1象限の第1点（0、R）では、判別式dの初期値d0を推定できます
。d0= F（1、R–0.5）= 1 –（R–0.5） 2–R2 = 3-2R
円の中心が原点にないことを考慮して、計算された座標を変換する必要があります。
3.6実験コード
（1）角度DDA円生成アルゴリズム
/
//角度DDA圆生成算法
/
void CLiHuchenView::OnDdacircle()
{
// TODO: Add your command handler code here
CDC *pDC=GetDC();//获取设备指针
int xc=200,yc=200,r=50,c=RGB(0,0,255);///定义圆心,角度，半径，圆的颜色蓝色
int x=0,y=r,n=r; //赋初值
double rc = (double)r; //修改类型
double z=1.0/rc; //得到微分角度
double a=x,b=y; //将x，y分别赋予a，b
double tmp; //定义变量
while(n > 0)
{
//八个区域点，画点
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
tmp=a;
a-=b*z; //计算下一点横坐标
b+=tmp*z; //计算下一点纵坐标
x = (int)(a);
y = (int)(b);
n--;
}
if(x == y)
{
//八个区域点，画点
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
}
ReleaseDC(pDC);//指针释放
}
（2）中点円生成アルゴリズム：
/
//中点圆生成算法
/
void CLiHuchenView::OnMidpointcircle()
{
// TODO: Add your command handler code here
CDC *pDC=GetDC();//获取设备指针
int xc=300,yc=300,r=50,c=RGB(255,0,0);///定义圆心，半径，圆的颜色红色
int x,y;//定义变量x，y
float d;//定义中点带入圆的值d
x=0;y=r;d=1.25-r;//赋初值
//八个区域点，画点
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
//画圆
while(x<=y)
{
//判断d的正负
if(d<0)
{
d+=2*x+3;
}
else
{
d+=2*(x-y)+5;
y--;
}
x++;
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
}
ReleaseDC(pDC);//指针释放
}
（3）Bresenham円生成アルゴリズム：
/
//Bresenham圆生成算法
/
void CLiHuchenView::OnBresenhamcircle()
{
// TODO: Add your command handler code here
CDC *pDC=GetDC();//获取设备指针
int xc=100,yc=100,r=50,c=RGB(0,255,0);///定义圆心，半径，圆的颜色绿色
int x=0,y=r,p=3-2*r;//赋初值
//画圆
while(x<y)
{
//八个区域点，画点
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
//判断p的正负
if(p<0)
{
p+=4*x+6;
}
else
{
p+=4*(x-y)+10;
y--;
}
x++;
if(x==y)
pDC->SetPixel((xc+x),(yc+y),c);//(x,y)
pDC->SetPixel((xc-x),(yc+y),c);//(-x,y)
pDC->SetPixel((xc+x),(yc-y),c);//(x,-y)
pDC->SetPixel((xc-x),(yc-y),c);//(-x,-y)
pDC->SetPixel((xc+y),(yc+x),c);//(y,x)
pDC->SetPixel((xc-y),(yc+x),c);//(-y,x)
pDC->SetPixel((xc+y),(yc-x),c);//(y,-x)
pDC->SetPixel((xc-y),(yc-x),c);//(-y,-x)
}
ReleaseDC(pDC);//指针释放
}
3.7実験結果の表示
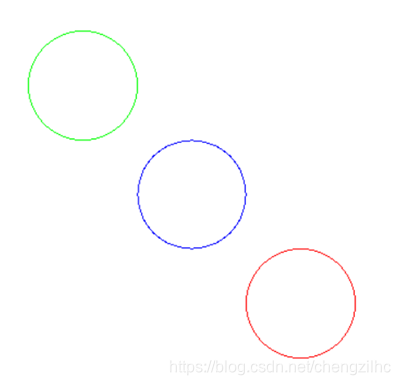赤：中点線アルゴリズム
緑：ブレゼンハムのアルゴリズム
青：角度微分法（DDA法）