MATLAB - FFT (transformée de Fourier rapide)

Connaissances de base
FFT est la transformée de Fourier rapide, qui réduit la quantité de calcul de DFT en utilisant la périodicité et la réductibilité. Les plus courants sont l'algorithme radix-2 extrait par le temps (DIT-FFT) et l'algorithme radix-2 extrait par la fréquence (DIF-FFT).

1. Utilisez la fonction intégrée fft pour effectuer une transformée de Fourier rapide
Si la séquence connue $X=[4,3,2,6,7,8,9,0]$ , trouver$X\left(k\right)=Le\; code\; DFT\left[x\right(n)\; ]$
est très simple, seulement deux lignes

x=[4,3,2,6,7,8,9,0];
xk=fft(x)

Généralement, pour MATLAB, si vous voulez qu'il affiche le résultat, n'ajoutez pas de point-virgule à la partie calcul.
2. Dessinez le diagramme amplitude-fréquence d'une DFT à 128 points.
Le signal connu est composé d'un signal sinusoïdal de 15 Hz avec une amplitude de 0,5 et d'un signal sinusoïdal de 40 Hz avec une amplitude de 2. La fréquence d'échantillonnage des données est de 100 Hz. Essayez de dessiner un diagramme amplitude-fréquence de N=128 points DFT.
Explication sur les codes suivants

f=(0:N-1)'*fs/N;

Parmi eux, (0:N-1)' est un vecteur ligne obtenu en générant un vecteur colonne dont la longueur est N et dont l'intervalle est 1. fs/N fait référence à l'intervalle de fréquence dans le domaine fréquentiel.
Si la séquence de N points x(n) (n=0,1,...,N-1) est obtenue à la fréquence d'échantillonnage fs(Hz). Sa FFT est aussi une séquence de N points, c'est-à-dire X(k) (k=0,1,...,N-1), alors la valeur de fréquence réelle correspondant au Kème point est : f=k*fs /
N

clc;
fs=100;
Ts=1/fs;%采样时间间隔
N=128;
n=0:N-1;
t=n*Ts;    %x不是直接关于n的函数，因为是固定的采样时间点
x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);

y=fft(x,N);
f=(0:N-1)'*fs/N;
stem(f,abs(y));

Résultats d'exécution

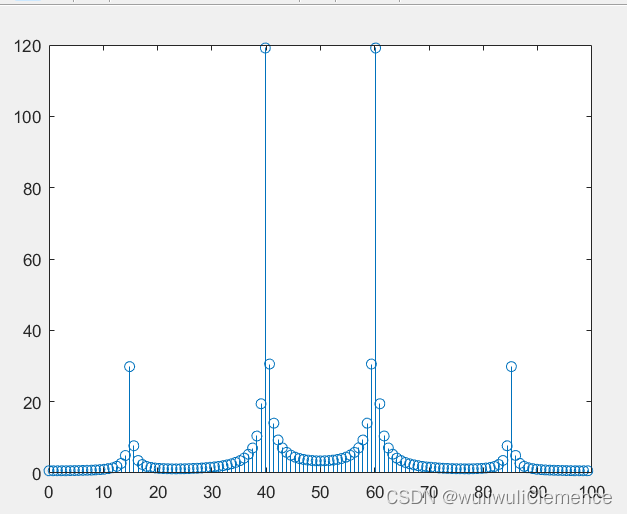
On peut également voir que le spectre d'amplitude est symétrique par rapport à fN.
3. Analyse du bruit du spectre de puissance à l'aide de FFT
On sait que le signal avec bruit de mesure $x\left(t\right)=sdans\left(2\pi f1t\right)+sdans\left(2\pi f2t\right)+2w\left(t\right)$ où f1=50Hz, f2=120Hz, w(t) est un signal aléatoire avec une valeur moyenne nulle et une variance 1, la fréquence d'échantillonnage est de 1000Hz et le nombre de points de données N=512. Essayez de tracer le spectre de puissance d'un signal.
Ce qui suit présente quelques fonctions et connaissances de base :
conj(Y)
conj(Y) est une fonction dans MATLAB, ce qui signifie prendre le nombre complexe conjugué de chaque élément de Y. Si Y est un tableau réel, renvoie lui-même. Dans le traitement du signal, les nombres conjugués complexes sont souvent utilisés pour le traitement de la transformée dans le domaine fréquentiel.
Trouvez la puissance
P=Y.*conj(Y)/512 ;
notez qu'il s'agit d'une multiplication de points.
En traitement du signal, la puissance peut être exprimée comme l'énergie moyenne d'un signal. Pour un signal à temps discret, son énergie peut être exprimée comme la somme de ses carrés d'amplitude, à savoir :
$$E=\sum _{n=0}^{N-}|X[n]{|}^2$$
où,$N$ est le nombre de points d'échantillonnage du signal,$x\left[n\right]$ est le signal au temps$La\; valeur\; échantillonnée\; de\; n$ . Ici$|X[n]{|}^2$ signifie paire$x\left[n\right]$ prend la longueur modulo au carré.
Si vous voulez calculer la puissance moyenne du signal, vous pouvez diviser son énergie totale par le nombre de points d'échantillonnage, à savoir :
$$P=\frac{}{N}=\frac{}{N}\sum _{n=0}^{N-}|X[n]{|}^{2PP}$$
ici$P$ représente la puissance du signal.
Dans le code,$Y$ représente la transformée de Fourier discrète du signal, c'est-à-dire la représentation dans le domaine fréquentiel, son amplitude$|Y|$ représente la contribution du signal sur chaque composante fréquentielle. Afin de calculer le spectre de puissance du signal,$Y$ transforme sa grandeur au carré, c'est-à-dire$|Oui{|}^2$ . Merci à$Y$ contient les informations de fréquence positive et de fréquence négative, il doit donc être conjugué, c'est-à-dire prendre le nombre complexe conjugué de la partie de fréquence négative, puis le multiplier par la partie de fréquence positive, c'est-à-dire Y ⋅ conj ⁡ ( Y ) Y \$Oui\cdot \mathrm{conj}\left(Y\right)$ . Enfin, divisez le résultat par le nombre de points d'échantillonnage$N$ , le spectre de puissance$P$ :
$$P=\frac{Oui\cdot \mathrm{conj}(Y}{N}$$
PP ici$P$ est une longueur$Un\; vecteur\; de\; N$ représentant la puissance du signal à chaque composante de fréquence.
randn
andn est une fonction de MATLAB utilisée pour générer un nombre aléatoire de distribution normale standard avec une moyenne de 0 et une variance de 1. Par exemple, une matrice aléatoire de distribution normale standard de taille 3x3 peut être générée à l'aide du code suivant :
A = randn(3,3);
Code complet

clc;
t=0:0.001:0.6;%设置步进与时间区间
x=sin(2*pi*50*t)+sin(2*pi*120*t);%根据已知写出信号的表达式
noise=randn(1,length(t));%生成均值为零、方差为1的随机信号，也就是噪声
y=x+noise;%带有噪声的信号
subplot(121);
plot(t,y);

fs=1000;
Y=fft(y,512);%512点的FFT
P=Y.*conj(Y)/512;%求功率
f=(0:255)*fs/256%由上面的分析可知，频谱关于奈奎斯特频率对称，所以取其中一半
subplot(122);
plot(f,P(1:256))%功率随频率的变化，即功率谱图,绘制出一半

Résultats en cours :

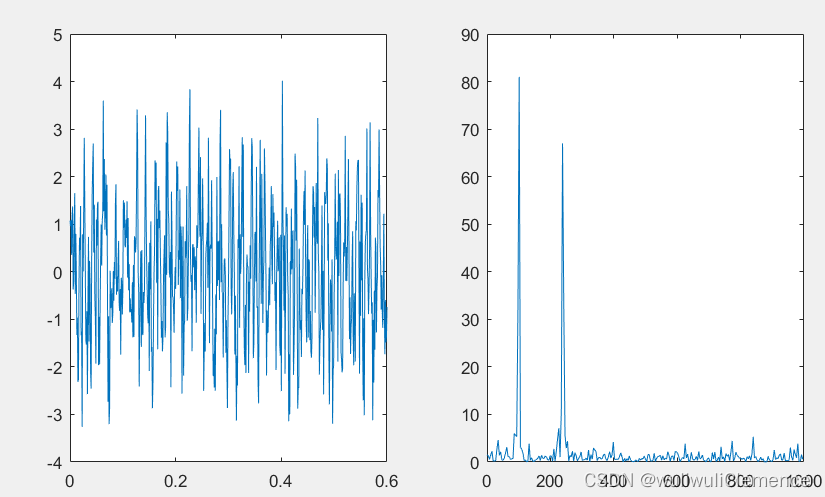
4. Effet de la longueur de la séquence et de la longueur FFT sur le spectre du signal
Signal connu $x\left(t\right)=\mathrm{0,5}sdans\left(2\pi f1t\right)+2sdans\left(2\pi f2t\right)$
Parmi eux, f1 = 15 Hz, f2 = 40 Hz et la fréquence d'échantillonnage est de 100 Hz.
Dessinez son spectre d'amplitude dans les conditions suivantes.
Avec la fondation précédente, voici un
code

nlength=32;
nfft1=32;
nfft2=128;
fs=100;
Ts=1/fs;
n=0:nlength-1;
t=n*Ts;

x=0.5*sin(2*pi*15*t)+2*sin(2*pi*40*t);

y1=fft(x,nfft1);
f1=(0:31)*fs/32;
subplot(211);
Y1=abs(y1);
plot(f1(1:16),Y1(1:16));

y2=fft(x,nfft2);
f2=(0:127)*fs/128;
subplot(212);
Y2=abs(y2);
plot(f2(1:64),Y2(1:64));

Résultats d'exécution

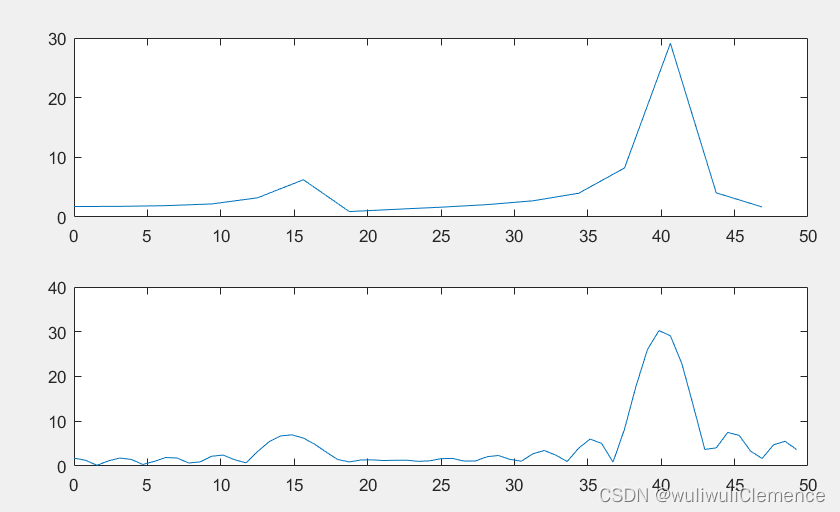
Analyse
des résultats Plus il y a de points d'échantillonnage, plus le spectre de fréquences est lisse.
Remarque
Lorsque vous dessinez un graphique, vous devez analyser s'il s'agit d'un graphique de spectre ou d'une certaine transformation.Le but est de distinguer qui est la variable dépendante et qui est la variable indépendante.