1. Definición de programación dinámica e ideas básicas.
La programación dinámica es un método de solución que descompone problemas complejos en subproblemas simples.
La idea básica de la programación dinámica: generalmente se utiliza para resolver problemas con ciertas propiedades óptimas, tratando de resolver cada problema una sola vez, una vez calculada la solución a un determinado subproblema, se memoriza y almacena de manera que el mismo subproblema -Se necesita un problema la próxima vez. Al resolver el problema, consulte la tabla directamente. La programación dinámica resuelve problemas de abajo hacia arriba (de forma iterativa en lugar de recursiva), evitando cálculos repetidos.
Para la recursividad, estos subproblemas se resuelven y luego las soluciones de los subproblemas se combinan para obtener la solución del problema original. La diferencia es que estos subproblemas se superponen y, una vez que se resuelve un subproblema, se puede resolver nuevamente.
Por lo tanto, podemos almacenar las soluciones a estos subproblemas, e independientemente de si el subproblema se usa más adelante, siempre que se calcule, los resultados se completarán en la tabla. La próxima vez que lo uses, utiliza los resultados directamente. Ésta es la idea básica del método de programación dinámica.
Ejemplo:
# 动态规划实现斐波那契数列
def fib(n):
# 递推公式的边界条件
if n == 0 or n == 1:
return n
dp = [0, 1, 0]
for i in range(1, n):
sum = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = sum
return dp[1]
print(fib(10))
# 时间复杂度:O(n)
# 空间复杂度:O(1)
# 递归思路
def fib(n):
if n == 0 or n == 1:
return n
return fib(n-1) + fib(n-2)
print(fib(10))
# 时间复杂度:O(2^n)
# 空间复杂度:O(n)2. Pasos básicos de la programación dinámica.
1. Determine la matriz que puede guardar los resultados de la fórmula recursiva o recursiva y el significado de los subíndices. Generalmente se usa una matriz unidimensional (pregunta más simple) o una matriz bidimensional (un poco más difícil) para guardarlo, aquí siempre está representado por dp []. Entre ellos, debemos entender el dp unidimensional [i] (matriz correspondiente a la posición del índice). elemento), matriz bidimensional dp[i][j] (en una matriz bidimensional, en términos simples, es el elemento en la posición de índice correspondiente de la fila y columna);
2. Inicialización de la matriz dp. Para matrices unidimensionales y bidimensionales, el valor inicial puede ayudar la próxima vez que los resultados parezcan superpuestos.
Por ejemplo: Fibonacci dp[0] = 0, dp[1] = 1, luego dp[2] = dp[0] + dp[1].
3. Determine la ecuación de transición de estado (fórmula de recursión). La transferencia de estado consiste en derivar el estado de esta etapa (es decir, la conexión entre diferentes etapas) en función del estado de la etapa anterior. De hecho, aquí se determina si los resultados utilizados antes son aplicables en esta etapa.
Por ejemplo: fib(4) de Fibonacci se calcula recursivamente dos veces, ambas con el mismo método de cálculo fib(4) = fib(3) + fib(2), por lo que este método de cálculo es una fórmula recursiva. En nuestra normalización dinámica, guardamos el primer resultado del cálculo y usamos el resultado directamente la próxima vez.
4. Determine el orden transversal. Por ejemplo: el recorrido de Fibonacci es de adelante hacia atrás, determinar el orden del recorrido puede obtener resultados más rápido.
5. Tome la matriz dp como ejemplo. Después de completar los pasos anteriores, podemos dar algunos ejemplos para deducir, o después de completar el código, podemos usar el editor de código. Yo uso vscode y pycharm para depurar el código.
Aquí, LeetCode explica estos cinco pasos.
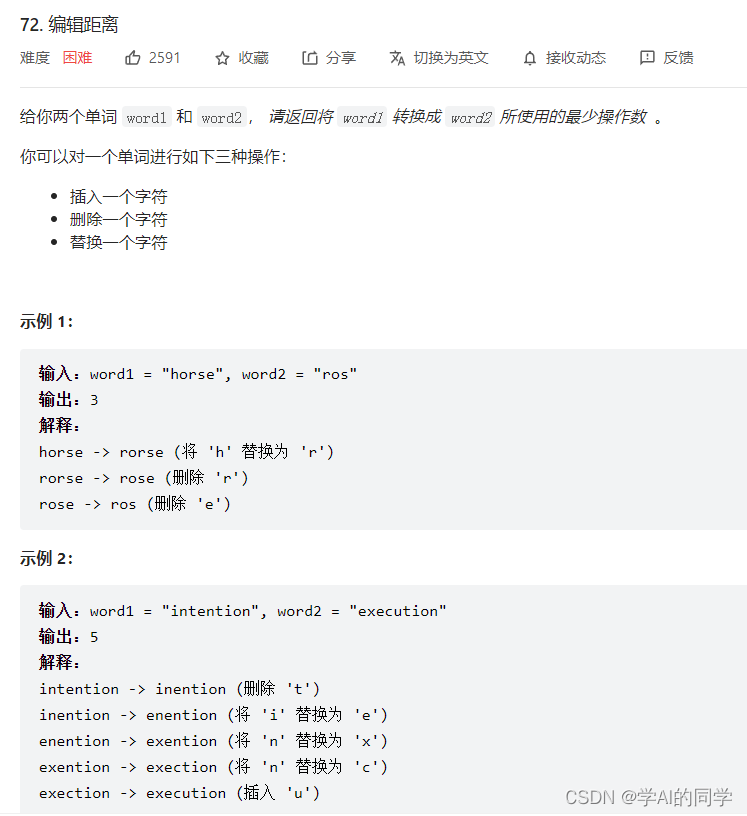
Paso 1: Determine la matriz dp y cree una matriz con m+1 filas y n+1 columnas para almacenar los operandos de cada cálculo. Debido a que palabra1 y palabra2 existen para realizar operaciones relacionadas, podemos usar una matriz bidimensional para convertir palabra1 en palabra2 y guardar la cantidad mínima de operaciones utilizadas.
dp = [[0] * (n+1) for i in range(m+1)Aquí, debe comprender el significado del subíndice dp[i][j] : la distancia mínima de edición entre los primeros i caracteres de palabra1 (subíndice i-1) y los primeros j caracteres de palabra2 (subíndice j-1), por ejemplo: palabra1 = 'op', palabra2 = 'app', luego dp[2][2]=X, que representa la distancia de edición mínima entre 'op' y 'ap', es decir, la cantidad mínima requerida para convertir 'op' a 'ap' operar.
Paso 2: Determine el valor inicial de la matriz dp. Para implementar la inicialización en la tabla, es necesario comprender la relación entre dp [i-1] [j-1], es decir, dp [i] [j].
Por ejemplo: si queremos encontrar el primer carácter dp[i][j] correspondiente a palabra1 y palabra2 para operar, necesitamos encontrar el operando mínimo del paso anterior, que es dp[i-1][j-1 ] Sin embargo, el elemento correspondiente está vacío, por lo que cuando determinamos el valor inicial, debemos considerar la situación de dp[i-1][j-1] = 0.
Entonces, ahora podemos determinar que el elemento de la primera fila del valor inicial es el operando del carácter vacío que se convierte en palabra2 después de la operación de suma, y el elemento en la primera columna es el operando en el que palabra1 se convierte en la cadena vacía después de la operación de eliminación. .
| Fila: palabra1 Columna: palabra2 |
" " nulo |
a | ap | aplicación | aplicar | manzana |
| " " nulo |
0 | 1 | 2 | 3 | 4 | 5 |
| oh | 1 | |||||
| op | 2 | |||||
| opp | 3 | |||||
| oppa | 4 |
dp[0][0] = 0 # 第一个元素赋值为0
for i in range(m+1): # 对word1里的元素全部做删除操作
dp[i][0] = i
for j in range(n+1): # 对word2里的元素进行添加操作
dp[0][j] = jEl tercer paso es determinar la fórmula de recursividad. La parte más difícil de esta pregunta es la fórmula de recursividad. Antes de comprender la fórmula de recursividad, primero determinamos las situaciones posibles:
1. Si palabra1[i-1] == palabra2[j-1] durante la conversión, no necesitamos realizar la operación. Podemos retener directamente el resultado del subíndice dp[i-1][j-1].Asignado hasta este momento, es decir, dp[i][j] == dp[i-1][j-1].
2. Cuando palabra1[i-1]!= palabra2[j-1], debemos considerar tres formas en que ocurren las operaciones.
Es decir: palabra1 reemplaza palabra1[i-1]: dp[i][j] = dp[i-1][j-1] + 1
word2 elimina un elemento: dp[i][j] = dp[i][j-1] + 1
Word1 elimina elementos: dp[i][j] = dp[i-1][j] + 1, lo que equivale a que word2 agregue un elemento.
| dp[i-1][j-1] | dp[i-1][j] |
| dp[i][j-1] | dp[i][j] |
¿Por qué + 1 aquí?
Esto se debe a que en estas tres operaciones, tenemos el último resultado retenido en la matriz dp y necesitamos resolver el resultado de dp [i] [j]. Finalmente se obtiene el valor mínimo de los operandos (el menor número de operandos) y se obtiene +1.
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1],dp[i][j-1],dp[i-1][j])+1El cuarto paso es determinar el orden transversal de la matriz. Obviamente, necesitamos combinar las cuatro fórmulas de recursividad y podemos saber que el orden transversal es de izquierda a derecha y de arriba a abajo.
Paso 5: Verificar y deducir mediante ejemplos
Aquí usamos word1='oppa' y 'apple' para la derivación.
| Fila: palabra1 Columna: palabra2 |
" " nulo |
a | ap | aplicación | aplicar | manzana |
| " " nulo |
0 | 1 | 2 | 3 | 4 | 5 |
| oh | 1 | 1 | 2 | 3 | 4 | 5 |
| op | 2 | 2 | 1 | 2 | 3 | 4 |
| opp | 3 | 3 | 2 | 1 | 2 | 3 |
| oppa | 4 | 3 | 3 | 2 | 2 | 3 |
Se puede decir que la mayoría de las preguntas sobre algoritmos de programación dinámica se basan en estos cinco pasos, por lo que debes prestar atención al significado de los cinco pasos.
Todavía necesitamos estudiar más preguntas para comprender mejor las ideas de la programación dinámica.
implementación del código Python:
def minDistance(word1, word2):
m = len(word1)
n = len(word2)
# 当word1为空的时候,word2的长度就是需要编辑的距离
if m == 0:
return n
# 当word2为空的时候,word1的长度就是需要编辑的距离
if n == 0:
return m
# 创建一个m+1行n+1列的数组
dp = [[0]*(n+1) for i in range(m+1)]
dp[0][0] = 0
# 从 word1[:i] 变成 空串(word2[:0]), 操作即**删除** i 次直到将 word1[:i] 删光到 空串
for i in range(1,m+1):
dp[i][0] = i
# 从 空串(word1[:0]) 变成 word2[:j], 操作即**插入** j 次直到将 空串 变成 word2[:j]
for j in range(1,n+1):
dp[0][j] = j
for i in range(1, m+1):
for j in range(1, n+1):
# 考虑字符是否相等
if word1[i-1] == word2[j-1]:
# 如果相等就是上一步操作的步数
dp[i][j] = dp[i-1][j-1]
else:
# 如果不相等就是附近三个最小值+1
dp[i][j] = 1+min(dp[i-1][j-1], dp[i-1][j], dp[i][j-1])
return dp[m][n]
s1 = "oppa"
s2 = "apple"
print(minDistance(s1,s2))Aquí, gracias a todos por navegar y, al mismo tiempo, gracias a todos los destacados expertos por brindarme información que me hizo comprender la planificación dinámica.
Si hay un artículo idéntico, informe al autor y adjunte un enlace. Adjuntaré el enlace a la posición correspondiente en este artículo. Gracias.