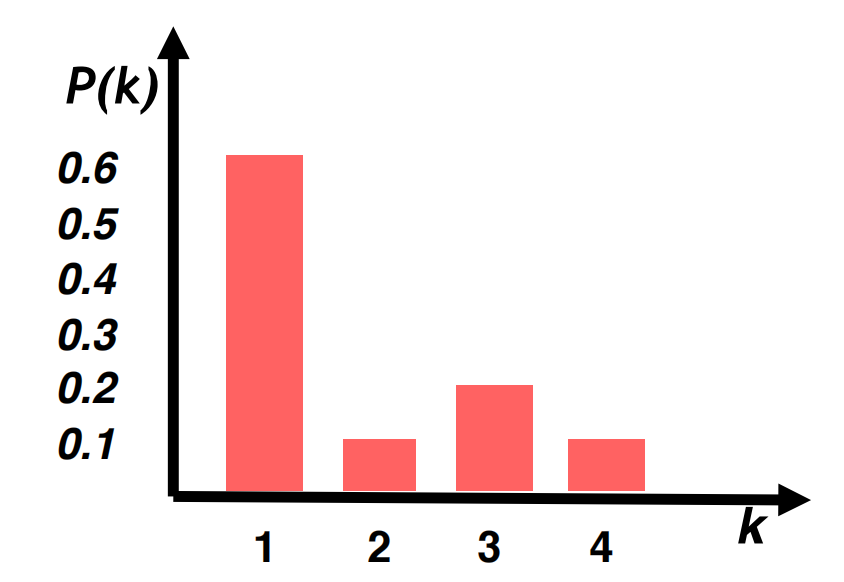
distribución de 1 grado
La distribución de grados p(k)p(k) de la red representa la probabilidad de que un nodo seleccionado aleatoriamente tenga un grado kk. Establecemos el número de nodos con grado kk Nk=♯ nodos con grado kNk=♯ nodos con grado k, y lo dividimos por el número de nodos NN para obtener la distribución de masa de probabilidad normalizada:
P(k)=Nk/N(k∈N)P(k)=Nk/N(k∈N)
Tenemos: ∑k∈NP(k)=1∑k∈NP(k)=1.
Para esta red:

El histograma de distribución de grados normalizado se puede expresar de la siguiente manera:
2 caminos
2.1 El camino del gráfico
La ruta (path) de un gráfico se refiere a una secuencia de nodos, de modo que cada nodo en la secuencia está vinculado al siguiente nodo en la secuencia (nota: la terminología aquí es diferente en diferentes libros de texto, y algunos libros de texto definen la ruta aquí como un paseo), y reservar el término "camino" para caminos simples). Las rutas se pueden representar de las siguientes maneras:
Pn={i0,i1,i2,…,in}Pn={(i0,i1),(i1,i2),(i2,i3),…,(in−1,in)}Pn={i0,i1 ,i2,…,pulgadas}Pn={(i0,i1),(i1,i2),(i2,i3),…,(pulgadas−1,pulgadas)}
Un camino puede intersecarse a sí mismo pasando el mismo borde varias veces. Como se muestra en la figura a continuación, más caminos ABDCDEG se cruzan consigo mismo.
Tenga en cuenta que las rutas en gráficos dirigidos solo pueden seguir la dirección de los bordes.
2.2 Número de caminos
El número de caminos se define como el número de caminos entre los nodos uu y vv. Encontramos que existe una relación entre el poder de la matriz de adyacencia y el número de caminos.
- Matriz de conteo de rutas de longitud h=1h=1 (aquí h puede entenderse como saltos): solo es necesario verificar si existe un enlace de longitud 11 entre uu y vv, es decir
H(1)uv=UvHuv(1)=Uv
- Matriz de conteo de caminos con longitud h=2h=2: Es necesario verificar si existe un camino de longitud 22 entre uu y vv, es decir contar kk que cumpla AukAkv=1AukAkv=1.
H(2)uv=∑k=1NAukAkv=[A2]uvHuv(2)=∑k=1NAukAkv=[A2]uv
- Matriz de conteo de caminos de longitud hh: Es necesario examinar si existe un camino de longitud hh entre uu y vv, es decir, para todo <k1,k2,⋯,kh que satisface Auk1Ak1k2….Akh−1v=1Auk1Ak1k2….Akh −1v=1 −1><k1,k2,⋯,kh−1>secuencia para contar.
H(h)uv=[Ah]uvHuv(h)=[Ah]uv
La conclusión anterior es válida tanto para grafos dirigidos como no dirigidos. El teorema anterior explica que si hay un camino más corto entre uu y vv, entonces su longitud es la kk más pequeña que hace que AkuvAuvk no sea cero.
Una inferencia adicional muestra que una forma sencilla de encontrar todos los caminos más cortos en un gráfico de n nodos es realizar cálculos de potencia sucesivos en la matriz de adyacencia AA del gráfico uno por uno, hasta la n−1n−1ª vez, observe que cada La potencia a la que un elemento se vuelve positivo por primera vez. Esta idea tiene una aplicación importante en el algoritmo de ruta más corta de Folyd-Warshall.
2.3 Distancia
La distancia (distancia) entre dos nodos en el gráfico se define como el número de aristas en el camino más corto entre los dos puntos (si los dos puntos no están conectados, la distancia generalmente se define como infinito).
Para la siguiente figura tenemos la distancia HB entre BB y DD, D=2HB, D=2, la distancia hA entre AA y XX, X=∞hA, X=∞.
Tenga en cuenta que las distancias en los gráficos dirigidos deben seguir la dirección de los bordes. Esto conduce a una distancia no simétrica en el gráfico dirigido. Por ejemplo, en la siguiente figura tenemos hA,C≠hC,AhA,C≠hC,A.
Definimos la distancia máxima entre dos nodos cualesquiera como el diámetro del gráfico.
2.4 Longitud de trayecto media
La longitud de ruta promedio de un gráfico conectado no dirigido (componentes conectados) o un gráfico fuertemente conectado dirigido (componentes fuertemente conectados) se define como:
h¯=12Emax∑i,j≠ihijh¯=12Emax∑i,j≠ihij
Aquí hijhij es la distancia del nodo ii al jj. Emax=n(n−1)2Emax=n(n−1)2, aquí el coeficiente 22 en 2Emax2Emax es opcional, y el método de definición de diferentes materiales didácticos es diferente.
Al calcular la longitud promedio de la ruta, generalmente solo calculamos la distancia entre los nodos conectados (es decir, ignoramos las rutas con una longitud "infinita")
2.5 Encontrar el camino más corto
Para gráficos no ponderados, podemos buscar la ruta más corta en el gráfico mediante la búsqueda en amplitud (BFS).
- Comience en el nodo uu, etiquételo como hu(u)=0hu(u)=0 y póngalo en cola.
- Cuando la cola no está vacía:
- Quite el primer elemento vv de la cola, agregue sus vecinos sin marcar a la cola y márquelo como hu(w)=hu(v)+1hu(w)=hu(v)+1.
- Repetidamente.
Para gráficos ponderados, por supuesto, tenemos que buscar algoritmos como Dijkstra y Bellman-Ford, que no se repetirán aquí.
3 Coeficiente de agrupamiento
El coeficiente de agrupamiento del nodo ii puede entenderse intuitivamente como el porcentaje de vecinos del nodo ii que están conectados entre sí. Sea kiki el grado del nodo ii, entonces su coeficiente de agrupamiento CiCi se define como
Ci=2eiki(ki−1)Ci=2eiki(ki−1)
Aquí eiei es el número de aristas entre vecinos del nodo ii, tenemos Ci∈[0,1]Ci∈[0,1]. A continuación se muestran algunos ejemplos de coeficientes de agrupamiento:
El coeficiente de agrupamiento promedio de un gráfico se define como:
C=1N∑iNCiC=1N∑iNCi
4 Propiedades de las redes del mundo real
A continuación, veamos un ejemplo de red de información de envío y recepción de MSN (dirigida).

245 millones de usuarios registrados en la red, 180 millones de usuarios participaron en el chat y hubo más de 30 mil millones de respuestas. Más de 255 mil millones de mensajes interactivos.
conectividad
distribución de grados
Su distribución de grados está muy sesgada, con un grado medio de 14.414,4.
distribución de grados logarítmicos
coeficiente de agrupamiento
Aquí, para facilitar el trazado, definimos la abscisa como el grado kk, y la ordenada correspondiente CkCk como el valor promedio del coeficiente de agrupamiento CiCi de los nodos con el grado kk, es decir, Ck=1Nk∑i:ki= kCiCk=1Nk∑i:ki = kCi.
El coeficiente de agrupamiento promedio de toda la red es 0.110.11.
distribución de distancia
Entre ellos, la longitud de ruta promedio es 6.66.6, y se puede llegar al 90%90% de los nodos dentro de los 88 saltos.
referencia
[1] CS224W | Inicio
[2] Easley D, Kleinberg J. Redes, multitudes y mercados: razonamiento sobre un mundo altamente conectado [M]. Cambridge university press, 2010.
[3] Barabási A L. Network science[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2013, 371(1987): 20120375.
[4] 《图论概念梳理》