Regularización - penalización de norma de parámetro

regularizaciónLa definición de: "Una modificación del algoritmo de aprendizaje, dirigida a reducir el error de generalización en lugar del error de entrenamiento."
Comprensión intuitiva: la regularización es una estrategia utilizada para reducir el sobreajuste del modelo.

Lo que sigue es uno de los métodos más comunes de regularización - $L^1$ y$L^2$ regularización.
Así llamado$L^1$ y$L^2$ regularización, en realidad usa $L^1$ y$L^2$ norma, para normalizar los parámetros del modelo (peso$w$ ) de un método.

Norma, podemos entenderlo como una extensión del concepto de distancia entre dos puntos en el espacio. Por ejemplo peso $w$ , es un vector de alta dimensión, y también puede entenderse como un punto en el espacio.La distancia de este al origen, si es la distancia de Manhattan, es L 1 L^$L^1$ norma, si es distancia euclidiana, es$L^2$ norma.

• $L^0$ norma: el número de elementos distintos de cero en el vector.
• $L^1$范数：$||W|{|}_{}=|w_{}|+|w_{}|+...+|w_{}|$ (distancia Manhattan)
  
• $L^2$范数：$||W|{|}_{}=\sqrt{|w_{}{|}^2+|w_{}{|}^2+...+|w_{}{|}^2}$(Distancia euclidiana)
  

Porque es el peso ww lo que realmente provoca el problema de sobreajuste$w$ , por simplicidad, en la siguiente discusión, solo nos enfocamos en$w$ _

1. Regularización de parámetros L2

$L^{La\; regularización\; de\; 2}$ parámetros a menudo se denominacaída de pesoy funciona agregando un término de regularización$\Omega \left(\theta \right)=\frac{}{2}||ww|{|}_2^{}$, acercando los pesos al origen.

Así que aquí viene la pregunta: $L^{¿Por\; qué\; la\; regularización\; de\; 2}$ parámetros se llama decaimiento de peso? ¿Cómo atenuó el peso?

Función de pérdida: $J(ww,b)$
Actualización del peso:$ww=ww-ϵ\cdot {▽}_{}J\left(ww\right)$
Para la función de pérdida$J(W,b)$ , queremos encontrar un conjunto de parámetros$({ww}^{\ast },b^{\ast })$来 minimizar$J(ww,b)$ _

Por simplicidad, solo consideramos el peso $w$ , entonces la función objetivo del modelo es:
$$\tilde{j}(ww;Xx,yy)=\frac{}{2}{w}^{T}w+J(ww;Xx,yy)$$ donde,$a\in [0,\infty )$ se llamatasa de descomposición, es el término de penalización de la norma de compensación $\Omega$ y función objetivo estándarJJHiperparámetros para la contribución relativa de$J.$será$\alpha$ se establece en 0 para indicar que no hay regularización;$Cuanto\; mayor\; sea\; \alpha$ , mayor será la sanción de regularización correspondiente. Durante el proceso de solución, escalamos el término de penalizaciónΩ \OmegaHiperparámetroα \alpha$de\; \Omega$$\alpha$ para controlar$L^2$ La fuerza de la caída del peso.

El gradiente correspondiente a la función objetivo es: ${▽}_{}\tilde{j}(ww;Xx,yy)=unaw+{▽}_{}J(ww;Xx,yy)$

Use el descenso de gradiente de un paso para actualizar los pesos: $w\leftarrow w-ϵ(\alpha w+{▽}_{}J(ww;Xx,yy))$
可种写法是：$w\leftarrow (1-ϵa)w-ϵ{▽}_{}J(ww;Xx,yy)$

Podemos ver que la adición de la disminución de peso provocará la modificación de las reglas de aprendizaje, y el vector de peso se reducirá antes de que se realice cada actualización de gradiente.

De esta forma, para la atenuación del peso, podemos entenderlo intuitivamente como: la atenuación del peso consiste en agregar algunos elementos de penalización para castigar el peso y castigar un poco por cada aprendizaje, para que el peso no sea demasiado grande.

La introducción anterior es $L^{2.}$ La influencia de la regularización en los pesos en el descenso de gradiente de un solo paso, entonces, ¿qué tipo de influencia tendrá en el proceso general de entrenamiento?
En primer lugar, debemos aclarar nuestro objetivo.Nuestro objetivo es controlar los parámetros para que el valor del parámetro no sea demasiado grande. Siguiendo esta línea de pensamiento, podemos dar$w$ define un dominio factible, sea$W$ toma valores en esta zona.

Región factible: $||ww|{|}_{}-C\le 0$ (es decir,$wLa\; distancia\; desde\; el\; punto\; correspondiente\; a\; w$ en el espacio al origen es$\le C$ 's. )

A continuación, entendemos L 2 L^2 desde la perspectiva del método del multiplicador de Lagrange$L^2$ El efecto de la regularización en el proceso formativo global.
Podemos escribir la función objetivo como:$\tilde{j}(ww,yo)=J\left(ww\right)+\lambda (||ww|{|}_{}-c)$

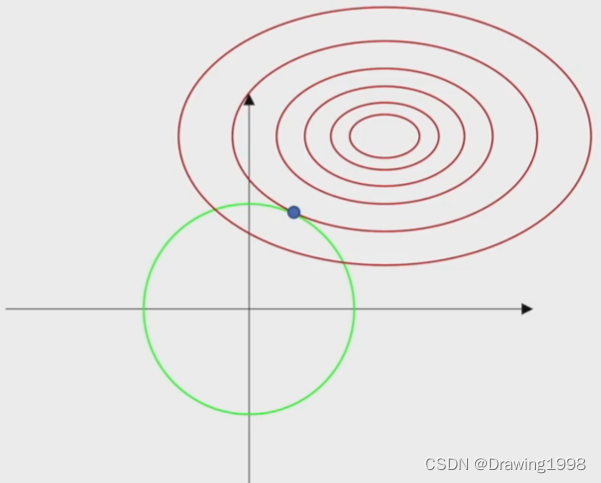
En esta figura, la línea roja es la línea de contorno de la función de pérdida, y la línea verde es lo que le damos a wwEl rango de dominio factible definido por$w\; .$

• CC en la función objetivo$C$ determina el peso que le damos awwEl tamaño del rango de dominio factible definido por$w\; ;$
• $\lambda$ es el multiplicador de Lagrange, y su función es ajustar el gradiente correspondiente a la condición de restricción para que sea igual al gradiente de la función de pérdida.
  

De esta imagen podemos ver claramente que a través de $L^2$ norma para limitar los pesoswwEl rango de valores de$w$$El\; valor\; de\; w$ es demasiado grande para reducir el fenómeno de sobreajuste del modelo.

Porque $L^{La\; región\; factible\; correspondiente\; a\; la\; norma\; 2}$ es un conjunto convexo, y el método de descenso de gradiente también es un método de optimización convexo, por lo que usamos$L^2$ norma par$w$ está restringido, el problema que queremos resolver sigue siendo un problema de optimización convexo.

Podemos pensar en la penalización de la norma del parámetro como una restricción impuesta a los pesos.
Supongamos que encontramos el valor óptimo de la tasa de decaimiento $a^{\ast }$ , por lo general no conocemos el coeficiente de decaimiento del peso (es decir, la tasa de decaimiento$a^{\ast }$ ) tamaño de región restringido, porque$a^{El\; valor\; de\; \ast }$ no puede decirnos directamenteCCvalor de$c$En principio podemos resolver$C$ , pero$C$ y$a^{\ast }$ La relación entre depende deJJforma de$j$
Aunque no conocemos el tamaño exacto de la región restringida, se puede determinar aumentando o disminuyendo$\alpha$ para expandir o contraer aproximadamente la región restringida. α \alphamás grande$\alpha$ , obtendrá una región restringida más pequeña,$\alpha$ , se obtendrá una región restringida más grande.
A veces queremos usar límites explícitos en lugar de penalizaciones. Por ejemplo, podemos modificar el algoritmo de descenso (como el algoritmo de descenso de gradiente estocástico) para que primero calcule$El\; paso\; descendente\; de\; J\left(\theta \right)$ , entonces$\theta$ se proyecta para satisfacer$\Omega \left(\theta \right)<$El punto más cercano de$C.$Si sabemos qué tipo de$C$ es adecuado, y no quiero perder el tiempo buscandoCCα \ alfade$C$$valor\; alfa$ , esto puede ser muy útil.

Extracto de la Sección 7.2 de "Aprendizaje profundo"

2. Regularización de parámetros L1

con $L^2$ La regularización es similar, usando$L^1$ Cuando la regularización decae el peso, también escalamos el término de penalizaciónΩ \OmegaHiperparámetroα \alpha$de\; \Omega$$\alpha$ para controlar$L^1$ La fuerza de la caída del peso.
Término de penalización$\Omega$ se puede expresar como:$Oh=||w|{|}_{}=\sum |w_{}|$

La función objetivo del modelo se puede expresar como:
$$\tilde{j}(ww;Xx,yy)=\alpha ||\_ww|{|}_{}+J(ww;Xx,yy)$$

Gradiente correspondiente: (en realidad subgradiente)
$${▽}_{}\tilde{j}(ww;Xx,yy)=\alpha sign\left(ww\right)+{▽}_{}J(ww;Xx,yy)$$ donde$firmar(\_\_\_ww)$ simplemente tomawwEl signo de cada elemento de$w\; .$

Use el descenso de gradiente de un paso para actualizar los pesos: $w\leftarrow w-ϵ\left(\alpha syogramonorte\right(ww)+{▽}_{}J(ww;Xx,yy)$
可种写法是：$w\leftarrow w-ϵ\alpha syogramonorte\left(ww\right)-ϵ{▽}_{}J(ww;Xx,yy)$

Podemos ver que $L^1$ El efecto de la regularización y$L^2$ no es lo mismo,$L^2$ La regularización es$w$ escala linealmente, y$L^1$ regularización es agregar un$firmar(\_\_\_ww)$ constantes del mismo signo.

Los modelos lineales simples tienen una función de costo cuadrática, que podemos representar mediante la serie de Taylor.
Suponemos que el gradiente correspondiente a la función objetivo es la etapa de la serie de Taylor que se aproxima a la función de costo de un modelo más complejo, entonces el gradiente se puede escribir como: ▽ w J ~ ( w ) = H ( w − w ∗ ) \bigtriangledown_w\widetilde{J}(\pmb{w}) = H(w - w^* ${▽}_{}\tilde{j}\left(ww\right)=alto(ancho-w^{\ast })$
Entre ellos,$H$ es la función de pérdida$J$ en$w^{}$La matriz hessianaen${}^{\ast }$ .

Suponemos que la arpillera es diagonal y que los datos de entrada del modelo se han procesado previamente para eliminar la correlación entre las características de entrada. Entonces podemos simplemente poner $L^1$ La aproximación cuadrática de la función objetivo regularizada se descompone en una suma sobre los parámetros:
$$\tilde{j}(ww;Xx,yy)=J({ww}^{\ast };Xx,yy)+\sum \left[\frac{}{2}{H}_{yo,}\right(w_{}+w_i^{}{)}^2+\alpha |w_{}|]$$
La solución analítica de la función (para cada dimensión$i$）可以表示为：
$$w_{}=firmar(w\_\_\_{}_i^{})máximox(|w_i^{}|-\frac{}{H_{yo,}},0)$$
Hay dos resultados posibles:

1. $|w_i^{}|-\frac{}{H_{yo,}}\le Cuando\; 0$ , wi w_ien la función objetivo después de la regularización$w_{}$El valor óptimo de es $w_{}=0$ ,$L^1$ plazo de regularización will$w_{}$empujado a 0, de modo que el $Las\; contribuciones\; de\; las\; funciones\; i$ se cancelarán.
2. $|w_i^{}|-\frac{}{H_{yo,}}\ge 0$ ,$L^1$ El plazo de regularización no cambiará$w_{}$empujado a 0, pero solo en $w_{}$Muévete en la dirección de $\frac{}{H_{yo,}}$distancia.

De esta manera, después de $L^1$ Después de la regularización obtendremos una solución másescasa(escasa), por lo que$L^1$ La regularización también se usa ampliamente ende características.

A continuación, analizamos $L^1$ La influencia de la regularización en el proceso global de formación:
con$L^2$ La regularización es similar, damos$w$ define un dominio factible, sea$W$ toma valores en esta zona.

Región factible: $||ww|{|}_{}-C\le 0$ (es decir,$wLa\; distancia\; desde\; el\; punto\; correspondiente\; a\; w$ en el espacio al origen es$\le C$ 's. )

En esta figura, la línea roja es la línea de contorno de la función de pérdida, y la línea verde es lo que le damos awwEl rango de dominio factible definido por$w\; .$

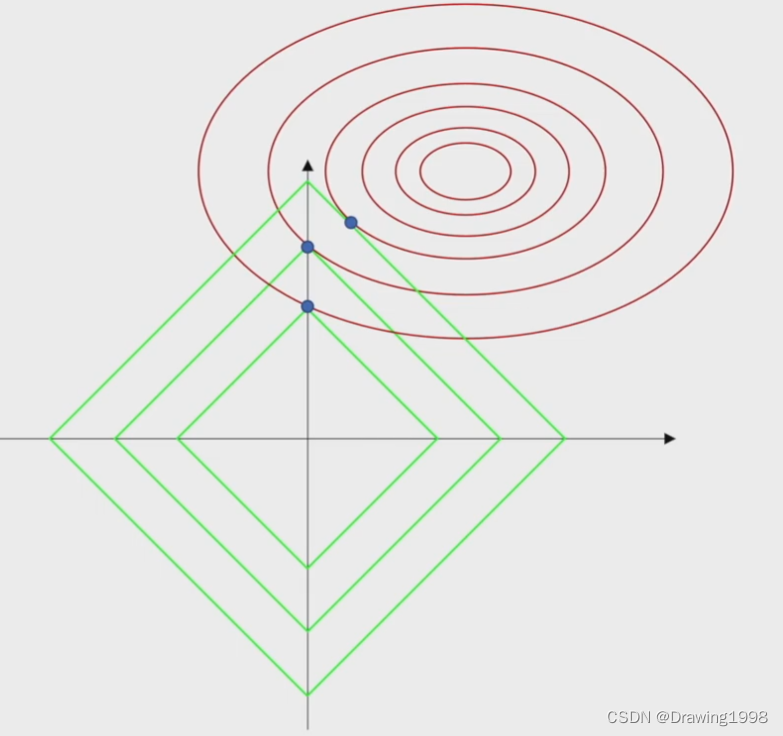
De esta figura también podemos ver que $L^1$ Regularización El punto donde el rango definido por el parámetro es tangente a la línea de contorno de la función de pérdida es más probable que esté en el eje de coordenadas, lo que hará que el peso sea$Algunos\; elementos\; de\; w$ tienen valores, y algunos elementos son 0, lo que hará que solo funcione una parte de las funciones de entrada, no todas las funciones.

3. Penalización de norma de parámetro

Para resumir la discusión anterior: la estrategia de regularización basada en la norma de parámetro penalización se pasa a la función objetivo $JAgregar$ un término de penalización$\Omega \left(\theta \right)$ para limitar la capacidad de aprendizaje del modelo, reduciendo así la aparición del fenómeno de sobreajuste.
Denotamos la función objetivo regularizada como$\tilde{j}$:
$$\tilde{j}(ww;Xx,yy)=J(ww;Xx,yy)+\alpha \Omega \left(\theta \right)$$ entre ellos,$a\in [0,\infty )$ se denomina tasa de atenuación, que es el término de penalización de la norma de compensación$\Omega$ y función objetivo estándarJJHiperparámetros para la contribución relativa de$J.$será$\alpha$ se establece en 0 para indicar que no hay regularización;$Cuanto\; mayor\; sea\; \alpha$ , mayor será la sanción de regularización correspondiente. Durante el proceso de solución, escalamos el término de penalizaciónΩ \OmegaHiperparámetroα \alpha$de\; \Omega$$\alpha$ para controlar$L^2$ La fuerza de la caída del peso.

En el caso de las redes neuronales, a veces es deseable usar una penalización separada para cada capa y asignar un $coeficiente\; alfa$ . Dado que encontrar los hiperparámetros múltiples correctos es costoso, para reducir el espacio de búsqueda usamos el mismo decaimiento de peso en todas las capas.