Función de pérdida y regularización.

Más del 90% de este artículo proviene de un artículo sobre redes neuronales en la Universidad de Stanford, y registra el contenido de aprendizaje para su futura revisión.

Directorio:

• Función de pérdida
• Regularización
• Aplicación de la regularización en la función de pérdida.
• Softmax y SVM
• Entropía cruzada
• Estimación de máxima verosimilitud (MLE)
• Resumen

Primero, la función de pérdida

Este artículo utilizará un ejemplo para comprender cuál es la función de pérdida: para conocer

el significado específico de los parámetros en este artículo, consulte el artículo de aprendizaje y resumen de redes neuronales , pero no lo repetiré aquí.
De la figura podemos encontrar que este conjunto particular de pesas W no es muy efectivo, dando al gato una puntuación muy baja. Usaremos la función de pérdida (a veces llamada función de costo o función objetivo) para medir nuestra insatisfacción con los resultados. Intuitivamente, si no lo hacemos bien al clasificar los datos de entrenamiento, la pérdida será grande; si lo hacemos bien, la pérdida será pequeña.
Hay varias formas de definir la función de pérdida:
MSE (error cuadrático medio):

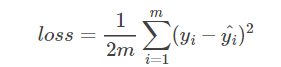
MSE es más fácil de usar en problemas de regresión lineal.
Máquina de vectores de soporte multiclase (SVM):
esta función puede garantizar que cada imagen obtenga la clase correcta más alta que la clase incorrecta Δ. Para diferentes muestras, la función de pérdida de la i-ésima muestra se define como:

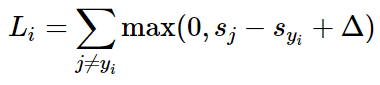
dar un ejemplo para comprender cómo funciona esta función. Supongamos que tenemos tres categorías y obtenemos tres puntajes s = [13, -7, 11], y la primera categoría es la categoría correcta. Al mismo tiempo, asumimos una variable Δ (un hiperparámetro) definida anteriormente = 10. Sustituyendo la función de pérdida anterior, obtenemos dos elementos:

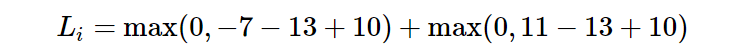
No es difícil darse cuenta de que el primer elemento obtiene un 0 y el segundo elemento obtiene 8. Dado que el puntaje de clase correcto (13) es al menos 10 mayor que el puntaje de clase incorrecto (-7), la pérdida de esta combinación es cero. La diferencia es en realidad 20, que es mucho mayor que 10, pero al SVM solo le importa que la diferencia sea al menos 10; cualquier diferencia adicional más allá del límite estará limitada a cero por la operación máxima. El segundo cálculo [11-13 + 10] da 8. Es decir, incluso si el puntaje de la clase correcta es más alto que el de la clase incorrecta (13> 11), no será más alto que el puntaje esperado en 10. La diferencia es solo 2, por lo que la pérdida es 8 (es decir, qué tan alta es la diferencia para alcanzar la diferencia). En resumen, la función de pérdida de SVM debería corregir el puntaje de la clase que se compara fácilmente con el puntaje de clase incorrecto en al menos Δ. Si este no es el caso, acumularemos pérdidas.
Para las redes neuronales, utilizamos una ecuación lineal para obtener el puntaje:

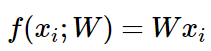
Entonces, podemos redefinir el formato de la función de pérdida: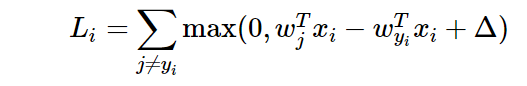
donde wj es el vector de la fila j del par W de la matriz (el vector correspondiente a la categoría j) transformado en Vector de columna Finalmente, a través de una imagen, la fórmula anterior se puede

entender más intuitivamente: todas las funciones de pérdida de muestra se integran en una función de pérdida completa:

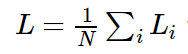
Softmax: se presentará a continuación.

Segundo, regularización.

Los siguientes son varios métodos comunes de
regularización : (1) regularización
L2 : la regularización L2 es la forma más común de regularización. Lo hace penalizando los términos cuadrados de todos los parámetros, es decir, agregando un elemento 1/2 λ w² a la función de pérdida, donde 1/2 se usa para aplicar λw en lugar de 2λw para cada w cuando se aplica el descenso de gradiente. La regularización de L2 tiene una característica atractiva, que es alentar a todas las entradas en la red a tener una parte de ella, en lugar de usar alguna entrada en una gran cantidad. Finalmente, tenga en cuenta que en la actualización de parámetros del método de descenso de gradiente, el uso de la normalización de L2 finalmente significa que cada peso está decayendo linealmente: W + = -λ * W hasta 0.
(2) Regularización de L1 El
aumento en la regularización de L1 es λ | w |, y a veces podemos usar L1 y L2 al mismo tiempo. L1 tiene una propiedad muy excelente, puede usarse en el proceso de optimización, de modo que el vector de peso se vuelve escaso. En otras palabras, L1 eventualmente puede hacer la entrada de subconjunto disperso más importante, ignorando el ruido. Por el contrario, el vector de peso final de la regularización de L2 suele estar disperso, en pequeños números. En la práctica, si no le importa la selección explícita de funciones, la regularización de L2 funciona mejor que L1.
(3) Las restricciones de la norma máxima
imponen un límite superior absoluto en el tamaño del vector de peso de cada neurona, y usan el descenso de gradiente para imponer restricciones. En la práctica, actualizamos el parámetro w normalmente, pero forzamos el parámetro w a estar en un cierto rango. Su característica es que incluso cuando la velocidad de aprendizaje se establece demasiado alta, la red no "explotará" porque la actualización siempre es limitada .
(4) La deserción es
un método simple para evitar el sobreajuste de la red neuronal (p, que complementa otros métodos (L1, L2, maxnorm). Al entrenar, se activa manteniendo una neurona con una cierta probabilidad p (hiperparámetro) , O configúrelo en 0. La dificultad de aprendizaje es relativamente alta, la implementación específica puede referirse a Abandono: una forma simple de prevenir redes neuronales

Tercero, la aplicación de la regularización en la función de pérdida:

Supongamos que hemos encontrado una matriz de peso que es 0 para todas las funciones de pérdida de categoría. En este momento, puede ocurrir un problema. La matriz de peso no es estrictamente única y puede parecer que muchos W hacen que la clasificación de la muestra sea correcta.
Lo primero que debemos aclarar aquí es que si algunos parámetros W clasifican correctamente todos los ejemplos, cualquiera de estos parámetros se multiplica por λ (λ> 1) porque esta transformación extiende todas las fracciones de manera uniforme. Por ejemplo, si la diferencia de puntaje entre una clase correcta y la clase incorrecta más cercana es 15, entonces multiplicar todos los elementos de W por 2 dará como resultado una nueva diferencia de 30.
¿Cómo encontramos la única matriz de peso segura W? Aquí necesitamos agregar una función de pérdida regularizada R (W) a

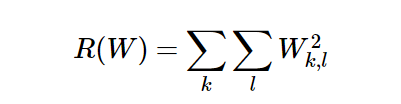
la función de pérdida. La expresión de la función de pérdida completa es: La

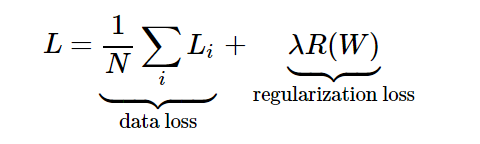
expansión general es:

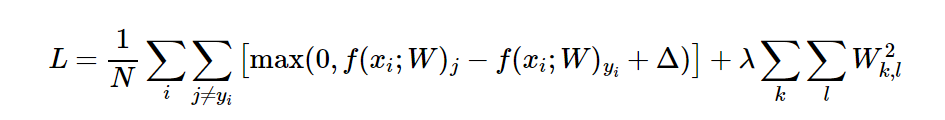
donde N es el número de muestras de entrenamiento y λ es el hiperparámetro . El castigo regularizado tiene muchas propiedades excelentes. La característica más atractiva es que el castigo con pesos más grandes ayuda a mejorar la capacidad de generalización, lo que significa que ninguna dimensión de entrada puede tener un impacto muy grande en el puntaje solo.
Supongamos que tenemos un vector de entrada x = [1,1,1,1], dos vectores de peso w1 = [1,0,0,0], w2 = [0.25,0.25,0.25,0.25]. Entonces wT1x = wT2x = 1 para que los dos vectores de peso obtengan el mismo producto puntual, pero la pérdida L2 de w1 es 1. La pérdida L2 de w2 es 0.25. Por lo tanto, de acuerdo con la penalización de L2, se prefiere el vector de peso w2 porque logra una menor pérdida de regularización. Intuitivamente, esto se debe a que los pesos en w2 son más pequeños y más dispersos. Dado que la penalización L2 tiende a ser vectores de peso más pequeños y más dispersos, se alienta al clasificador final a considerar todas las dimensiones de entrada en lugar de centrarse solo en unas pocas dimensiones de entrada. Esto juega un papel importante para mejorar el rendimiento de generalización del clasificador y prevenir el sobreajuste.

4. Softmax y SVM

Softmax: si alguna vez has oído hablar de un clasificador de regresión logística binaria, entonces el clasificador Softmax es una generalización de este, con un clasificador de varias clases. A diferencia de la máquina de vectores de soporte que toma la salida f (xi, W) como la puntuación de cada clase (no calibrada y puede ser difícil de interpretar), el clasificador Softmax proporciona una salida más intuitiva (probabilidad de clase normalizada). Primero observe la forma de la función de pérdida: el

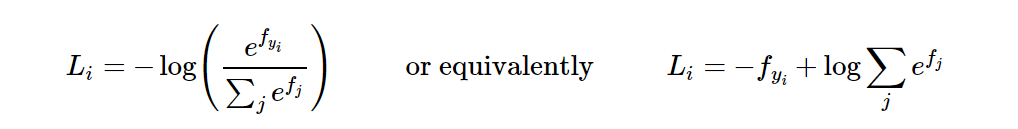
objetivo del clasificador Softmax es minimizar la entropía cruzada entre la probabilidad de que la clase sea probada y sus atributos verdaderos. Entre ellos, la entropía cruzada espera que la distribución de predicción se concentre en la respuesta correcta. Primero observe la siguiente expresión:

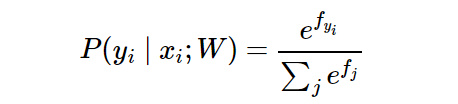
Se puede interpretar como la probabilidad (normalizada) asignada a la etiqueta correcta yi dada la imagen xi y parametrizada por w. Para comprender esto, recuerde que el clasificador Softmax interpreta la puntuación en el vector de salida f como una probabilidad de registro no normalizada. Por lo tanto, alimentar estas cantidades produce la probabilidad (no estandarizada) y luego se divide de modo que la suma de las probabilidades sea 1.
Desde una perspectiva probabilística, minimizamos la probabilidad logarítmica negativa de la clase correcta, que puede interpretarse como la realización de la estimación de máxima verosimilitud (MLE) . Para más detalles, vea la estimación del quinto módulo de máxima verosimilitud. Una buena característica de este método es que podemos
explicar que el término de regularización R (W) en la función de pérdida completa proviene de una matriz de peso anterior gaussiana W, en la que estamos realizando el máximo posterior (MAP) Se estima que el principio de seleccionar la función de registro aquí es la entropía cruzada. Los lectores que quieran profundizar en ella pueden referirse a ella ( el papel de la entropía cruzada en el aprendizaje automático ). Este artículo lo presentará brevemente en el próximo módulo.

Si desea implementar la función Softmax, debe prestar atención al proceso de escribir el código. Debido a la existencia del exponente, tanto el numerador como el denominador pueden ser números muy grandes. La operación de números grandes es inestable. Aquí se introduce el parámetro C para resolver este problema. La expresión se transforma de la siguiente manera:

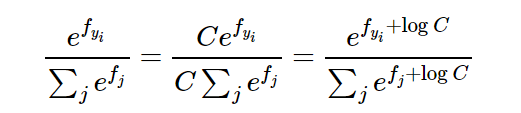
podemos elegir libremente el valor de c, que no cambiará ningún resultado, pero podemos usar este valor para mejorar el cálculo. Estabilidad numérica. Si el valor máximo en el resultado de la función se selecciona como C (el más utilizado), se puede entender bien a través del código:

f = np.array([123, 456, 789]) 
p = np.exp(f) / np.sum(np.exp(f)) # 出现数值不稳定问题

# 将最大值转换为0
f -= np.max(f) # f ——> [-666, -333, 0]
p = np.exp(f) / np.sum(np.exp(f)) # 结果不变，且过程安全

La siguiente es una comprensión más intuitiva de la diferencia entre los dos clasificadores:

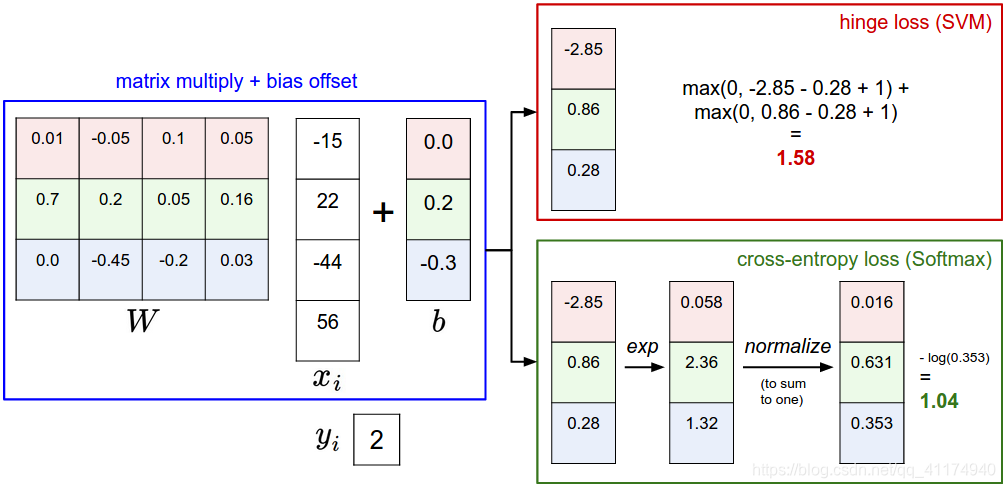
SVM:
estos puntajes se interpretan como puntajes de clase, y su función de pérdida alienta a la clase correcta (el azul indica la clase 2) a obtener puntajes más altos que otras clases. .
Clasificador Softmax:
interprete el puntaje de cada clase como una probabilidad de registro (no estandarizada) y luego fomente una probabilidad de registro alta (normalizada) de la clase correcta (equivalente a un número negativo bajo).
A diferencia de los cálculos de máquina de vectores de soporte donde los puntajes de todas las clases no están calibrados y no son fáciles de interpretar, el clasificador Softmax nos permite calcular las "probabilidades" de todas las etiquetas. La probabilidad se cita aquí porque el tamaño de probabilidad final también se ve afectado por el parámetro de regularización λ en la función de pérdida. Si la intensidad de regularización λ es alta, la penalización del peso W también aumentará, lo que hará que el peso se reduzca y la distribución de probabilidad sea más dispersa.

Cinco, entropía cruzada

(Extracto del papel de la entropía cruzada en el aprendizaje automático ) Un
resumen simple es: el problema de clasificación de la red neuronal se resume en un problema de clasificación único y un problema de clasificación múltiple: (por ejemplo)
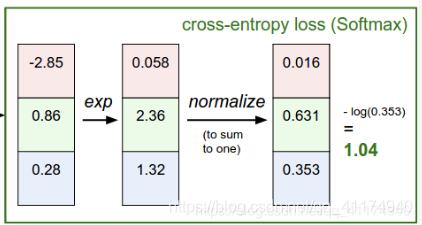
problema de clasificación única: continúe siguiendo el ejemplo al comienzo del artículo, suponiendo que el tipo de objetivo es tres Estos son gatos, perros y botes. Suponiendo que ahora hay una muestra de gatos, el valor predicho correspondiente es [0 (perro), 1 (gato), 0 (barco)], suponiendo que la P obtenida por el cálculo anterior es [0.3, 0.6, 0.1], cruce conocido La fórmula de entropía es:

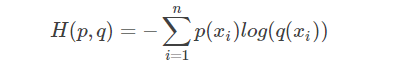
la función de pérdida (entropía cruzada) se puede obtener de acuerdo con la fórmula:

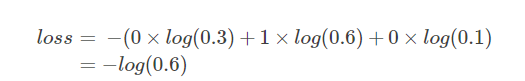
problema de clasificación múltiple:
continúe usando el ejemplo al comienzo del artículo, suponiendo que el tipo de destino es tres, es decir, gato, perro y barco. Suponiendo que ahora hay una muestra de gatos, el valor predicho correspondiente es [0 (perro), 1 (gato), 0 (barco)], suponiendo que la P obtenida por el cálculo anterior es [0.3, 0.6, 0.1], y clasificación única La etiqueta del problema es diferente, la etiqueta de la categoría múltiple es n-hot. Por ejemplo, una imagen puede tener un perro y un gato, por lo que es un problema de clasificación múltiple.
Pred aquí ya no se calcula mediante softmax, aquí se usa sigmoide. Normalice la salida de cada nodo a [0,1]. La suma de todos los valores Pred ya no es 1. En otras palabras, cada etiqueta se distribuye de forma independiente y no tiene efecto entre sí. Por lo tanto, la entropía cruzada se calcula por separado para cada nodo, y cada nodo tiene solo dos valores posibles, por lo que es una distribución binomial. Como se mencionó anteriormente, para una distribución especial como la distribución binomial, el cálculo de la entropía se puede simplificar.
Del mismo modo, el cálculo de la entropía cruzada también se puede simplificar, es decir,

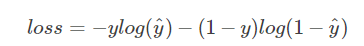
la pérdida de una sola muestra es loss = losscat + lossdog + loss boat

Sexto, estimación de máxima verosimilitud

( Artículo de referencia )
Declaración: Parte del contenido original del autor se copia directamente aquí, el propósito es compararlo con este artículo, para darle al lector una comprensión más clara.

En problemas prácticos, los datos que podemos obtener solo pueden tener un número limitado de datos de muestra, y la probabilidad previa y la probabilidad condicional de clase (la distribución general de varios tipos) son desconocidas. Cuando se clasifica en base a los únicos datos de muestra, un método factible es que primero necesitamos estimar la probabilidad previa y la probabilidad condicional de la clase.

La estimación de la probabilidad previa es relativamente simple, porque la red neuronal (aprendizaje supervisado) conoce el estado natural al que pertenece cada muestra. Estimación de la probabilidad condicional de la clase (muy difícil), las razones incluyen: la función de densidad de probabilidad contiene toda la información de una variable aleatoria, y los datos de la muestra pueden no ser muchos; la dimensión del vector de características x puede ser muy grande y así sucesivamente.

La estimación de máxima verosimilitud es un método de estimación de parámetros . Por supuesto, la selección de la función de densidad de probabilidad es muy importante, el modelo es correcto, cuando el área de muestra es infinita, obtendremos una estimación más precisa. El propósito de la estimación de máxima verosimilitud es utilizar resultados de muestra conocidos para inferir los valores de los parámetros que más probablemente (máxima probabilidad) conducen a tales resultados.

En la red neuronal, el valor del parámetro objetivo obtenido por la estimación de máxima verosimilitud es la matriz de peso W, y la probabilidad condicional de clase es (correspondiente a la entropía cruzada): el

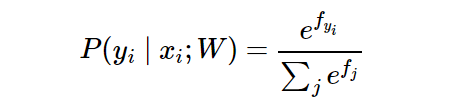
paso para resolver la función de máxima verosimilitud:

1. Estimación de ML: encuentre el valor de θ que maximice la probabilidad del conjunto de muestras.
   

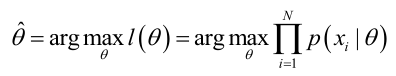
2. Para facilitar el análisis en la práctica,

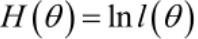
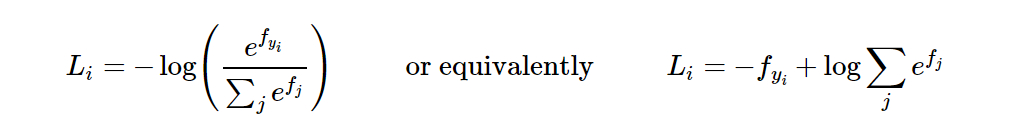
se define una función de probabilidad logarítmica (función de pérdida de Softmax (entropía cruzada)): dado que la segunda mitad de Li es un valor fijo, solo necesitamos optimizar Li = -fyi.
3. Existen múltiples parámetros desconocidos (θ es un vector),
entonces θ puede expresarse como un vector desconocido con componentes S:

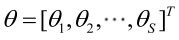
recuerde el operador de gradiente:

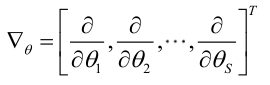
Si la función de probabilidad satisface la condición de derivabilidad continua, el estimador de máxima probabilidad es la solución de la siguiente ecuación.

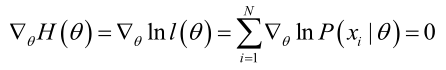
La solución de la ecuación es solo un valor estimado, y estará cerca del valor verdadero solo cuando el número de muestras tiende a ser infinito.

Para las redes neuronales, la estimación de máxima verosimilitud busca el operador de gradiente, es decir, la optimización del descenso de gradiente de la función de pérdida. El contenido específico de este artículo no se centra en la discusión, puede consultar mi resumen y aprendizaje de la red neuronal . Finalmente, se usa una red neuronal para calcular la probabilidad posterior de la muestra para predicción y clasificación.

6. Resumen

Este artículo presenta principalmente los dos clasificadores más comunes SVM y Softmax para explicar la función de pérdida en la red neuronal, de donde encontramos que la definición de la función de pérdida es que una buena predicción de los datos de entrenamiento es igual a una pequeña pérdida.
La diferencia de rendimiento entre la máquina de vectores de soporte y Softmax suele ser muy pequeña, y diferentes personas tendrán diferentes puntos de vista sobre qué clasificador funciona mejor. El clasificador Softmax nunca está completamente satisfecho con la puntuación que genera: la clase correcta siempre tiene una probabilidad más alta, y la clase incorrecta siempre tiene una probabilidad más baja, y la pérdida siempre es mejor. Sin embargo, una vez que se cumpla el límite, el SVM estará contento y no administrará micro puntajes precisos que excedan este límite.
Además, también presenta algunas fórmulas comúnmente utilizadas para la regularización y los pasos específicos de la estimación de máxima verosimilitud. Una vez finalizado el aprendizaje de la función de pérdida, es el problema de optimización. El problema de optimización en las redes neuronales a menudo se implementa mediante el método de descenso de gradiente. Para obtener más información, consulte la comprensión y el aprendizaje sobre el método de descenso de gradiente .