[Teoría de matrices] Norma y función de matriz (1)

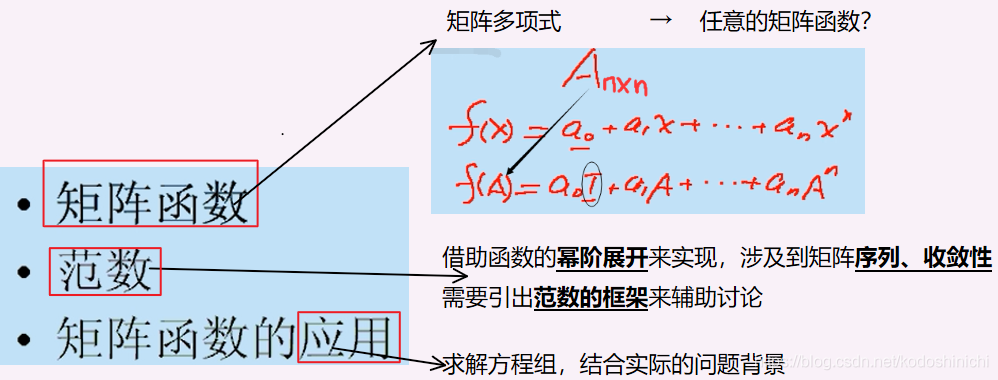
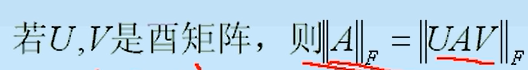El concepto de norma y la norma de función matricial.

En primer lugar, el contenido de este capítulo se resumirá de la siguiente manera:

resolvemos el problema de la función matricial a través del concepto de norma y usamos la función matricial para resolver muchos problemas prácticos.

---

1. Conceptos y definiciones

1. Norma y espacio lineal normalizado

(1) Norma: una función de valor real que satisface ciertas propiedades en un espacio vectorial

La propiedad 1 se llama definición positiva (positividad constante)
de la norma . La propiedad 2 se llama homogeneidad de la norma. Como k ∈ F, F puede ser un dominio de números complejos, el valor de k debería ser módulo. La
propiedad 3 es llamada la norma. La desigualdad del triángulo

(2) Espacio lineal normado

El espacio lineal que define la norma se llama espacio lineal normado.

2. Ejemplos de normas comunes y espacios lineales normativos

(1) La longitud en el espacio interior del producto es una especie de norma.

[Revisión] El espacio del producto interno es el espacio lineal que define el producto interno: si F ∈ R, es espacio euclidiano, si F ∈ C, es espacio unitario.

Debido a que la longitud del espacio interior del producto es la norma más común e importante , todos usamos la notación || · || en este capítulo cuando expresamos "norma".

Nota: Cuando se habla de norma, || · || no es la solo referencia a la longitud del vector.

(2) Ejemplos de normas en C ⁿ (transformación de p norma y norma)

Suponga que existe cualquier vector X = (x ₁ , x ₂ ,…, x _n ) ^T ∈ C ⁿ

①P familia de normas

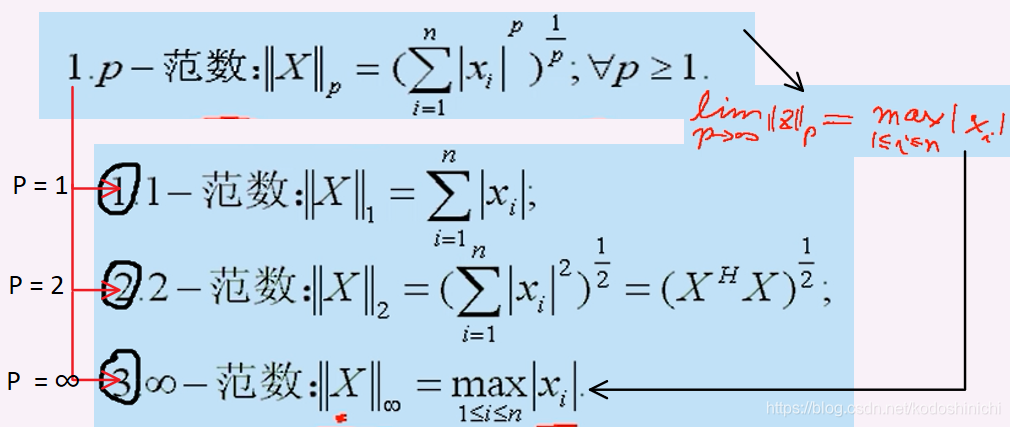
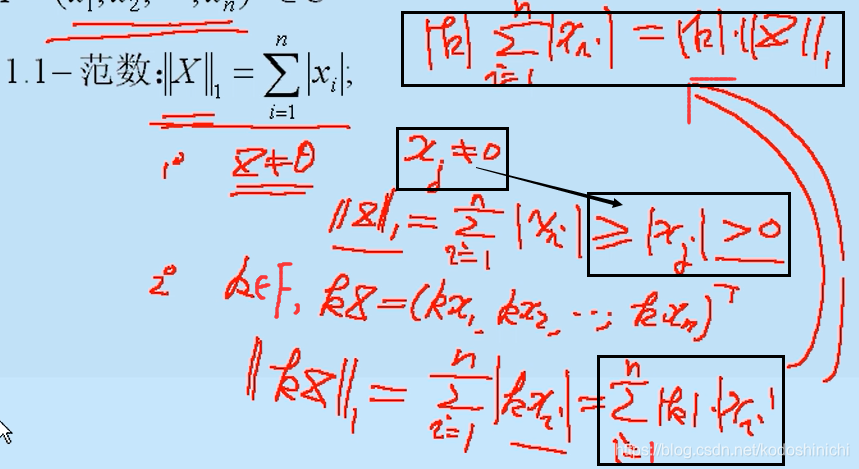
Con respecto a si la p-norma satisface las tres propiedades de la definición de la norma, a continuación se utiliza la norma 1 para ilustrar:

[Nota] Las propiedades de "definición positiva", "homogeneidad" y "desigualdad triangular" de la norma 1 de la naturaleza satisfactoria Lo anterior es la satisfacción de las propiedades correspondientes de la aritmética modular .

El lugar marcado con un recuadro negro en la figura de arriba es el punto clave de la prueba.

②La transformación de la norma

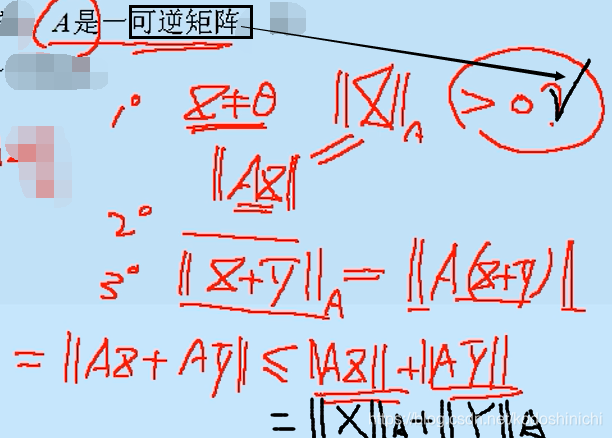
Para la definición de norma conocida en el espacio C ⁿ , se puede obtener otra definición de norma a través de una matriz invertible A.

La prueba breve es la siguiente:

Consejo: Para una matriz A invertible y un vector x distinto de cero, Ax ≠ θ debe ser verdadera . Se puede argumentar mediante el método de la contradicción.

(3) Definición de norma en cualquier espacio lineal

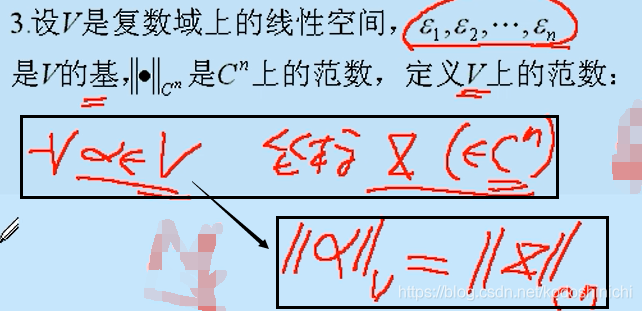
En otras palabras, para cualquier espacio lineal dado V (F∈C);
encuentre un conjunto de bases en este espacio V , las coordenadas de cualquier vector α en V en el conjunto de bases corresponden a X ;

entonces cualquier vector arbitrario en V La norma || α || _{V del} vector α se puede convertir en la norma del vector de coordenadas X (X∈C ⁿ ) en el espacio C ⁿ || X || _{C ^ n ^} .
ps En la sección anterior, discutimos muchas definiciones de normas que funcionan en el espacio C ⁿ , que se pueden seleccionar según sea necesario.

---

2. Norma y límite

Esta sección describe la necesidad de definir el concepto de "norma".
La definición de la norma es definir la secuencia del vector y el límite del vector.

1. Secuencia de matrices y convergencia

La convergencia de la secuencia de la matriz ps está relacionada con la definición de norma elegida.

2. Comparabilidad de normas

En una palabra, si las dos normas son comparables , entonces la convergencia de la secuencia matricial descrita bajo estas dos normas es equivalente .

Mirando hacia atrás en la definición de convergencia de secuencia de matriz, si se usan dos normas diferentes, ¿la misma secuencia de matriz convergerá a valores diferentes?
—— Con base en esto, proponemos la comparabilidad de normas.

(1) Definición

(2) Prueba y comprensión La
siguiente es una prueba de que "las dos normas son comparables ↔ el valor límite de la secuencia de la matriz bajo las dos normas es el mismo"

Consejo: Dado que la relación de desigualdad se da en la definición de "comparable", la prueba se basa principalmente en el criterio de sujeción del límite.

若 || η _i -η ₀ || → 0 ， 则 || η _i -η ₀ || '→ 0

Según la definición comparable:
|| η _i -η ₀ || '≤ (1 / k ₁ ) || η _i -η ₀ || → 0;
|| η _i -η ₀ ||' ≥ (1 / k ₂ ) || η _i -η ₀ || → 0;
según el criterio de sujeción, hay || η _i -η ₀ || '→ 0.

若 || η _i -η ₀ || '→ 0 ， 则 || η _i -η ₀ || → 0

La idea es la misma que la anterior:
|| η _i -η ₀ || ≤k ₂ || η _i -η ₀ || '→ 0;
|| η _i -η ₀ || ≥k ₁ || η _i - η ₀ || '→ 0;
Según el criterio de sujeción, hay || η _i -η ₀ || → 0

(3) Teorema

Cualesquiera dos normas en el espacio lineal de dimensión finita V son comparables.

---

3. Norma de la matriz

Antes de discutir la definición de norma del espacio lineal general, a continuación discutimos un espacio lineal más especial: la definición de norma en el espacio matricial.

1. La definición de normas matriciales comunes

(1) Matriz p-norma

Si la matriz se divide en filas o columnas , cada elemento de bloque puede aplicar la norma definida en el espacio C ⁿ antes , de modo que se pueda derivar la definición relevante de la norma de la matriz.

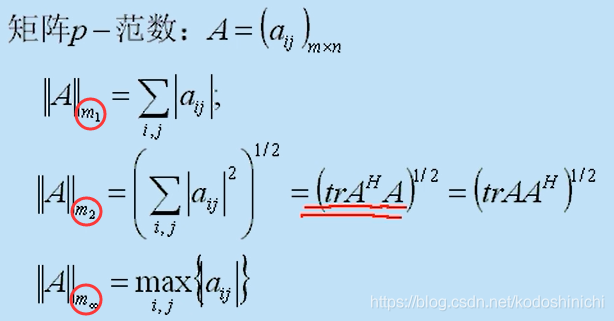
• Norma de Frobenuis (|| A || _m2 = || A || _F )

Entre ellos, se debe prestar especial atención a la
matriz 2-norma : la matriz 2-norma (norma de Frobenius) permanece invariante a la transformación unitaria.

[Prueba] La conclusión anterior puede ser probada por la definición de matriz 2-norma
|| A || _F = (trA ^H A) ^1/2 ;
|| UAV || _F = (tr (UAV) ^H (UAV) ) ^1/2 = (tr (V ^H A ^H U ^H UAV)) ^1/2
Debido a que U es una matriz unitaria, satisface U ^H U = I
|| UAV || _F = (trV ^H A ^H AV) ^{1 / 2}
Debido a que V también es una matriz unitaria, de modo que V ^H = V ^-1
se satisface || UAV || _F = (trV ^-1 A ^HAV) ^1/2 , debido a que V ^-1 A ^H AV y A ^H A deben ser similares, tienen los mismos valores propios. La traza (tr) de la matriz
ps es igual a la suma de los elementos diagonales principales de la matriz , que también es igual a la matriz La suma de todos los valores propios de .
Entonces la prueba está completa.

(2) Norma del operador

Si observa una matriz desde la perspectiva de la transformación lineal, entonces la matriz A _mxn ∈ C ^mxn puede considerarse como un vector X que pertenece al espacio C ^m y la asigna a un vector AX que pertenece al espacio C ⁿ .
Con base en el proceso de cálculo de este mapeo lineal, también queremos definir la norma correspondiente.

Aunque no entraré en la discusión aquí, los lectores deben cultivar una mentalidad. Después de definir la forma de norma mencionada anteriormente, si queremos reconocer que de hecho puede usarse como una norma, debemos pensar en las siguientes preguntas :

• || A || ¿Tiene sentido la norma?
• || A || ¿La norma satisface el axioma de la norma?

• Norma operador 1, norma operador 2 y norma operador 3
  

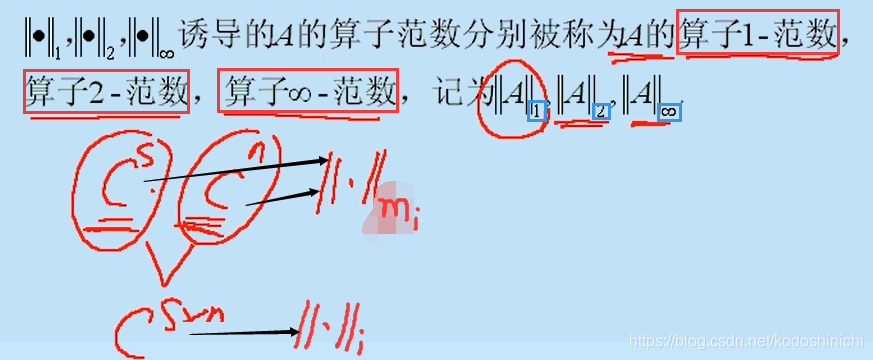
Cuando el espacio original y el espacio transformado toman || · || _mi (cierta norma de la matriz), entonces la norma del operador inducida por esto es || · || _i (el operador correspondiente cierta norma).
ps Aquí, debemos prestar atención a la forma en que se expresa el subíndice, y no lo confunda.

2. Compatibilidad de la norma matricial

Para las matrices, no solo tiene operaciones de suma y multiplicación de números, sino también operaciones de multiplicación.
Las operaciones numéricas de multiplicación y suma se basan en normas, las cuales están estandarizadas de acuerdo a la homogeneidad y desigualdades trigonométricas en la definición de normas;
sin embargo, las operaciones de multiplicación correspondientes a normas aún no han sido estandarizadas. Hasta ahora hemos propuesto el concepto de " compatibilidad".

(1) Definición de compatibilidad

(2) Teorema 1: La norma de la matriz 1, la norma 2 son compatibles y la norma infinita es incompatible

Demuestre que la norma del infinito de la matriz es incompatible, solo dé un contraejemplo

Como se muestra en la figura anterior, considere una matriz de 2 cuadrados de segundo orden, su propia norma infinita es 1; el resultado de su segunda multiplicación de potencia es una matriz de 2 cuadrados de segundo orden, y la norma de infinito correspondiente es 2.
Obviamente la desigualdad 2≤1x1 no está satisfecho.
Por tanto, incompatible.

Con respecto a la compatibilidad de la norma de la matriz 1 y la norma 2, no se da prueba en el video, los lectores pueden probarlo por sí mismos.

La idea de prueba puede aprender de las preguntas de prueba en el enlace a continuación y usar la definición y la naturaleza de la norma para escalar la desigualdad.
https://www.bilibili.com/read/cv4152269

(3) Teorema 2-Las normas del operador deben ser compatibles, lo que
significa que si para tres espacios lineales C ^s , C ^my C ⁿ , se definen tres normas en sus espacios || · || _Vs , || · || _Vm y || · || _Vn ;
entonces esta norma y tres, respectivamente, pueden inducirse como norma de operador es tres · || || _SXM , || · || _Sxn y || · || _mxn .

"La norma del operador debe ser compatible", es decir · || || _SXM , || · || _Sxn y || · || La norma _{del Banco de México MXN} tres necesariamente cumple con la definición de compatibilidad.

(4) Teorema 3: la solución de la norma del operador

• La norma del operador 1 es la suma máxima de la longitud del módulo
• La norma del operador 2 es el radio espectral de la matriz A ^H A
• La norma infinita del operador es la suma de filas de longitud modular más grande
  

Entre las tres normas de operador anteriores, la norma espectral es la más importante.
Hasta ahora, hay dos normas matriciales en las que debemos centrarnos: una es la norma de la matriz 2 (norma de Frobenuis) y la otra es la norma del operador 2 (norma espectral).

---

[Ejemplo] Resolver la norma matricial-1

De acuerdo con la definición de la norma, se puede sustituir en el cálculo en consecuencia.
Expanda la consulta, si se requiere la norma de la matriz 2 de A (es una matriz unitaria), entonces de acuerdo con la definición-
|| A || _m2 = (tr (A ^H A)) ^1/2 = (tr (I) ) ^1/2 = (n) ^media

• La norma de la matriz 2 de la matriz unitaria de orden n es n ^1/2
• La norma del operador 2 de matriz unitaria de orden n es 1

[Ejemplo] Resolver la norma matricial-2

[0]: Interprete el significado de la pregunta, el cuadro No. 0 es nuestro objetivo de prueba;
[1]: A es una matriz normal, entonces A debe transformarse en una diagonal por unitario Matriz de transformación, A está representada por una matriz diagonal y una matriz unitaria correspondientemente;
[2]: De acuerdo con la definición de la norma del operador 2, A ^H A y su radio espectral deben calcularse , y se puede saber que es similar a Λ ^H Λ;
[3] ： De acuerdo con el cálculo de la matriz diagonal, se obtiene la ecuación, y ambos lados se pueden resolver al mismo tiempo para cumplir con los requisitos de la pregunta.

• La norma del operador 2 de la matriz normal es el radio espectral de la matriz
  [Ejemplo] Resolviendo la norma de matriz-3 La
  
  prueba es clara, así que no entraré en detalles aquí y extraeré las conclusiones de los ejemplos.
  Para una matriz diagonal de bloques
• Su norma de matriz 2 es la suma de los cuadrados de las 2 normas de cada matriz de bloque y luego la raíz cuadrada
• La norma del operador 2 es el valor máximo de las 2 normas de cada operador de matriz de bloques.

Habilidades de memoria:
matriz 2 norma ↔ traza; operador 2 norma ↔ radio espectral ↔ toma el valor máximo
. La traza es la relación aditiva
en la diagonal del bloque ; el radio espectral es el valor máximo en la diagonal del bloque.