ラインフィーチャ
ライン機能:利点は、自然照明と視野角が不変であることです。また、より高度な機能により、追跡の堅牢性と精度も向上します。特に特定の人工シーン (屋内、廊下) やその他のシーンでは、テクスチャがない、または信頼性の低いテクスチャによって引き起こされる干渉を克服できます。
また、線分の検出とマッチングには特徴点に比べて時間がかかるという欠点もあります。同時に、バックエンドには標準および共通の SLAM 最適化およびループバック モジュールがありません。ライン フィーチャのマッチングも比較的困難です。たとえば、ライン セグメントは壊れやすく、強い幾何学的制約 (エピポーラ幾何制約など) がなく、欠落したテクスチャは強力に認識されません。
ライン特徴の代表的なものは PL-SLAM です この記事のリンクは次のとおりです:
PL-SLAM: Real-Time Monocular Visual SLAM with Points and Lines
著者はモスクワの Samsung AI Laboratory で修士を取得し、現在は英国のスラム企業に勤務しているAlexander Vakhitov
です。システム全体の枠組みを以下の図に示します。
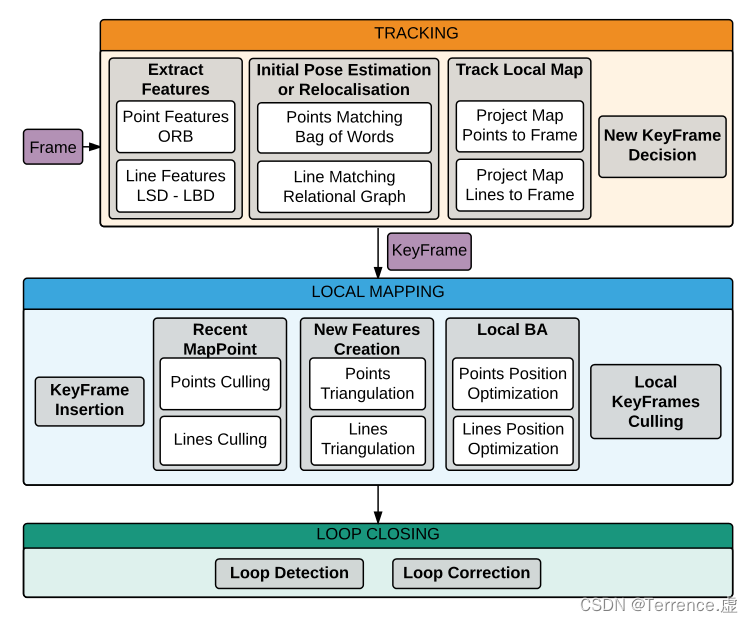
**
まとめ
** - 低テクスチャのシーンは、特に視覚的な SLAM の場合、点の対応に依存する幾何学的なコンピュータ ビジョン アルゴリズムの主なアキレス腱の 1 つであることはよく知られています。ただし、多くの環境では、テクスチャが低いにもかかわらず、ラインベースの幾何学的プリミティブを確実に推定できます。たとえば、都市や屋内のシーン、または構造化されたエッジが優勢ないわゆる「マンハッタン ワールド」などです。このホワイトペーパーでは、これらの状況に対処するためのソリューションを提案します。具体的には、精度と効率の両方の点でおそらく現在の最先端のソリューションである ORB-SLAM を基盤として構築し、その定式化を拡張して点と線の両方の対応を処理します。
入力画像からほとんどの点が消えた場合でも機能する解決策を提案します。興味深いことに、連続する 3 つのフレームで線の対応を検出するだけで初期化できます。私たちは、TUM RGB-D ベンチマークで私たちの手法と新しい初期化戦略を徹底的に評価し、ラインの使用により、テクスチャが不十分なフレームでの元の ORB-SLAM ソリューションのパフォーマンスが向上するだけでなく、効率を損なうことなく、ポイントとラインを組み合わせた連続フレームでも系統的にパフォーマンスが向上することを実証しました。
**
コンテンツ
**
1. ラインベースの SLAM
直線の記述には端点法が採用されていますが、結局のところ、現実には無限に伸びる直線に出会うことはほとんどなく、そのほとんどが線分であるため、直線を記述するには端点法を用いるのが合理的です。P , Q ∈ R 3 P, Q \in R^3 と仮定します。P 、Q∈R3は空間直線の 2 つの端点pd , qd ∈ R 2 p_d, q_d \in R^2pd、qd∈R2は画像内の投影座標です。さらに、pdh , qdh ∈ R 3 p_d^h, q_d^h \in R^3 をpdふ、qdふ∈R3は対応する同次座標です。次に、直線のパラメータを取得できます:
I = pdh × qdh ∣ pdh × qdh ∣ I=\frac{p_d^h \times q_d^h}{\left|p_d^h \times q_d^h\right|}私=∣ pdふ× qdふ∣pdふ× qdふ。
説明: (ベクトル(x, y, 1)は、幾何学的な意味で、3次元が定数となる平面上の2次元ベクトルとして理解できます。このように[2]次元のベクトルを[3]次元のベクトルで表現する方法、あるいは一般にn次元のベクトルをn+1次元のベクトルで表現する方法を同次座標表現といいます。] )
このようにして、ライン フィーチャに必要なパラメータを取得できます。次に、線を定義する線再投影誤差、つまり投影された線分の端点と画像内で検出された線の間の点から線までの距離の合計があります。 E line ( P , Q , I , θ , k ) = E pl 2 ( P , I , θ , k ) + E pl 2 ( Q , I , θ , k )
。E_{\text {行 }}(P, Q, I, \theta, k)=E_{pl}^2(P, I, \theta, k)+E_{pl}^2(Q, I, \theta, k) 。Eライン ( P 、質問、私は、私、k )=Eお願いします2( P 、私は、私、k )+Eお願いします2( Q 、私は、私、k ) E pl = IT π ( P , θ , K ) E_{pl}=I^T \pi(P, \theta, K)とします。Eお願いします=私T π(P,私、K ) E pl = IT π ( P , θ , K ) E_{pl}=I^T \pi(P, \theta, K
)としますEお願いします=私T π(P,私、K )。
其中, I I Iは前述の直線パラメータπ ( P , θ , K ) \pi(P, \theta, K)π ( P ,私、K )は空間点の画像平面への投影の座標で、 はそれぞれカメラの外部パラメータと内部パラメータです。理想的には、空間点の投影点は直線上にあるため、点間距離E pl = 0 E_{pl}=0Eお願いします=0、というより、点は線上にあります。
この計算により、2 つのライン間の再投影誤差が得られます。
ただし、実際の状況では、ライン間のオクルージョンや誤検出などの状況が常に発生するため、画像内で検出した端点pd 、 qd p_d、 q_dpd、qdおそらく空間線の端点P 、 QP 、 Qを使用P 、画像内のQの投影点が一致しないため、ここでは「検出された線の再投影誤差」(検出された線の再投影誤差) も定義されます。
E 行 , d ( pd , qd , I ) = E pl , d 2 ( pd , I ) + E pl , d 2 ( qd , I ) E_{\text {line }, d}\left(p_d, q_d, I\right)=E_{pl, d}^2\left(p_d, I\right)+E_{pl, d}^2\left(q_d, I\right)E行 、 d( pd、qd、私)=Epl 、d2( pd、私)+Epl 、d2( qd、I )
而E pl , d = IT pd E_{pl, d}=I^T p_dEpl 、 d=私T pd

命題: P , Q ∈ R 3 \mathbf{P}, \mathbf{Q} \in \mathbb{R}^3P 、Q∈R3 は、3D ライン フィーチャ上の 2 つの 3D 点を表します。p ~ 、q ~ ∈ R 2 \widetilde{\mathbf{p}}, \widetilde{\mathbf{q}} \in \mathbb{R}^2p
、q
∈R2は画像の画像平面上の投影点、l ~ \tilde{l}私~は投影線の係数です。
pd , qd ∈ R 2 \mathbf{p}_{\mathrm{d}}, \mathbf{q}_{\mathrm{d}} \in \mathbb{R}^2pd、qd∈R2は抽出されたライン フィーチャ (ライン セグメント) の 2 つの端点であり、これを測定値と呼びます。P d , Q d ∈ R 3 \mathbf{P}_{\mathrm{d}}, \mathbf{Q}_{\mathrm{d}} \in \mathbb{R}^3Pd、Qd∈R3は、これら 2 つの端点を 3D 空間内の対応する 3D 点に逆投影したもので、I は検出されたラインの係数です。
赤い線は点特徴の投影モデルX ∈ R 3 \mathbf{X} \in \mathbb{R}^3バツ∈R3は 3D 点であり、x ~ ∈ R 2 \widetilde{\mathbf{x}} \in \mathbb{R}^2 にバツ
∈R2
2. 線と点によるBA
X j ∈ R 3 X_j \in R^3を定義します。バツj∈R3は地図上のjj 番目j点。Ⅱ用iキーフレーム、X j X_jバツj画像平面の投影点は次のとおりです:
x ~ i , j = π ( X j , θ i , K ) \tilde{x}_{i, j}=\pi\left(X_j, \theta_i, K\right)バツ~私、 j=円周率( Xj、私私は、K )
其中, θ i \theta_i 私私は 为第 i i iキーフレームの外部パラメータ。特定の観測点xi 、 j x_{i, j}バツ私、 j、次の 3D 誤差を定義できます: ei , j = xi , j − x ~ i , j e_{i, j}=x_{i, j}-\tilde{x}_{i, j}e私、 j=バツ私、 j−バツ~私、 j
同様に、 j 番目のマップ内の線分の端点P j 、Q j P_j、Q_jを定義できます。Pj、Qj。i 番目のキー フレームにおけるその投影座標 (同次座標の形式) は次のように記録されます:
p ~ i , jh = π ( P j , θ i , K ) \tilde{p}_{i, j}^h=\pi\left(P_j, \theta_i, K\right)p~私、jふ=円周率( Pj、私私は、K )
q ~ i , jh = π ( Q j , θ i , K ) \tilde{q}_{i, j}^h=\pi\left(Q_j, \theta_i, K\right)q~私、jふ=円周率( Qj、私私は、K )
次に、特定の観測されたjjthに対して、j直線の端点pi 、 j 、 qi 、 j p_{i, j}、q_{i, j}p私、 j、q私、 j、そして観測されたラインパラメータI ~ i , j \tilde{I}_{i, j} を計算します。私~私、 jの場合、誤差ベクトルは次のように定義できます。
ei , j ' = ( I ~ i , j ) T ( K − 1 pi , jh ) e_{i, j}^{\prime}=\left(\tilde{I}_{i, j}\right)^T\left(K^{-1} p_{i, j}^h\right)e私、j「=(私~私、 j)T( K− 1p _私、jふ)
ei , j '' = ( I ~ i , j ) T ( K − 1 qi , jh ) e_{i, j}^{\prime \prime}=\left(\tilde{I}_{i, j}\right)^T\left(K^{-1} q_{i, j}^h\right)e私、j「=(私~私、 j)T( K− 1q _私、jふ)
(PS:这个 e i , j ′ , e i , j ′ ′ e_{i, j}^{\prime}, e_{i, j}^{\prime \prime} e私、j「、e私、j「の定義は個人的には間違っていると思います、なぜならpi , jh p_{i, j}^hだからですp私、jふ画像座標なのでK − 1 K^{-1}をかけるK− 1の結果は、画像平面ではなく、カメラ座標系の正規化平面の座標であるため、これは画像平面のI ~ i , j \tilde{I}_{i, j} と私~私、 j積の物理的な意味が間違っているので、個人的には、そのようなK − 1 K^{-1}はあってはならないと思います。K− 1)
この点は、後のヤコビアンを解く過程にも反映されます。
于是,我们最终的误差目标函数就可以写成:
C = ∑ i , j ρ ( e i , j ⊤ Ω i , j − 1 e i , j + e i , j ′ ⊤ Ω i , j ′ − 1 e i , j ′ + e i , j ′ ′ Ω i , j ′ ′ − 1 e i , j ′ ′ ) C=\sum_{i, j} \rho\left(\mathbf{e}_{i, j}^{\top} \Omega_{i, j}^{-1} \mathbf{e}_{i, j}+\mathbf{e}_{i, j}^{\prime}{ }^{\top} \Omega_{i, j}^{\prime}{ }^{-1} \mathbf{e}_{i, j}^{\prime}+\mathbf{e}_{i, j}^{\prime \prime} \Omega_{i, j}^{\prime \prime}{ }^{-1} \mathbf{e}_{i, j}^{\prime \prime}\right) C=∑私、 jr( e私、j⊤おお私、j− 1e私、 j+e私、j「⊤Ω _私、j「− 1e _私、j「+e私、j「おお私、j「− 1e _私、j「)
ここで、ρ ( ⋅ ) \rho(\cdot)ρ ( ⋅ )はロバストなコスト関数であり、この論文では Huber が使用されます。Ω i , j , Ω i , j ′ , Ω i , j ′ ′ \Omega_{i, j}, \Omega_{i, j}^{\prime}, \Omega_{i, j}^{\prime \prime}おお私、 j、おお私、j「、おお私、j「は、異なるスケールでのキーポイントと線分端点の共分散行列です。
