Ejercicio 2: Regresión Logística

Ejercicio 2: Regresión Logística

---

introducir

En este ejercicio, implementará la regresión logística y la aplicará a dos conjuntos de datos diferentes. También mejoraremos la solidez del algoritmo agregando regularización al algoritmo de entrenamiento y probaremos el algoritmo del modelo con situaciones más complejas.

Antes de comenzar el ejercicio, debe descargar los siguientes archivos para la carga de datos :

• ex2data1.txt - el conjunto de datos de entrenamiento para la primera mitad
• ex2data2.txt - la segunda mitad del conjunto de datos de entrenamiento

A lo largo del ejercicio, están involucradas las siguientes asignaciones obligatorias :

• Funciones para trazar datos categóricos 2D ----(3 puntos)
• Realizar la función Sigmoidea --------(5 puntos)
• Implementar la función de costo de regresión logística y la función de gradiente - (60 puntos)
• Realizar la función de predicción de regresión --------(5 puntos)
• Realice la función de costo de regresión logística regular ------- (27 puntos)

1 regresión logística

En esta parte del ejercicio, construirá un modelo de regresión logística para predecir si un estudiante será admitido en una universidad.

Suponga que usted es el director de un departamento en una universidad y decide las posibilidades de admisión de cada solicitante en función de los resultados de dos exámenes. Los datos históricos sobre solicitantes anteriores ya están disponibles y se pueden usar como un conjunto de entrenamiento para la regresión logística. Para cada fila de datos, contiene los puntajes de las dos pruebas del solicitante correspondiente y el resultado final de admisión.

En este ejercicio, debe crear un modelo de clasificación para predecir los resultados de admisión de los solicitantes en función de estos dos puntajes de prueba .

1.1 Visualización de datos

Antes de comenzar a implementar cualquier modelo algorítmico, lo mejor es visualizar primero los datos, lo que permitirá obtener de manera más intuitiva las características de los datos.

Ahora, debe escribir el código para completar el trazado de los datos , mostrando el gráfico que se muestra a continuación.

Puntos principales :

• Importe la biblioteca de python que debe usarse y leerá ex2data1.txtlos datos del archivo y mostrará las primeras 5 líneas
• El eje xy son las puntuaciones de los dos exámenes.
• Los ejemplos positivos y negativos deben mostrarse con diferentes marcadores (diferentes colores)

###在这里填入代码###
###主要实现要点1###
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
path = '/home/jovyan/work/ex2data1.txt'
data = pd.read_csv(path,header = None,names=['Exam 1','Exam 2','Admitted'])
data.head()

	examen 1	examen 2	Aceptado
0	34.623660	78.024693	0
1	30.286711	43.894998	0
2	35.847409	72.902198	0
3	60.182599	86.308552	1
4	79.032736	75.344376	1

###在这里填入代码###
###绘制数据散点图###
positive = data[data['Admitted'].isin([1])]
negative = data[data['Admitted'].isin([0])]
fig, ax = plt.subplots(figsize=(12,8))
# 正向类，绘制50个样本，c=‘b’颜色，maker=‘o’绘制的形状
ax.scatter(positive['Exam 1'], positive['Exam 2'], s=50, c='b', marker='o', label='Admitted')
ax.scatter(negative['Exam 1'], negative['Exam 2'], s=50, c='r', marker='x', label='Not Admitted')
ax.legend()# Legend 图例,获取label标签内容，如图右上角显示
ax.set_xlabel('Exam 1 Score')
ax.set_ylabel('Exam 2 Score')
plt.show()

1.2 Implementación

Como se puede ver en el diagrama de distribución de datos dibujado en la parte anterior del ejercicio, existe un límite de decisión más claro entre puntos de datos identificados de manera diferente. Ahora necesitamos implementar la regresión logística y usar la regresión logística para entrenar un modelo para predecir los resultados de la clasificación.

1.2.1 Función sigmoidea

Antes de comenzar oficialmente, primero entendamos una función: la función sigmoidea .
Recordamos que la definición del supuesto de regresión logística es:

Entre ellos, g representa una función lógica de uso común como la función sigmoidea (función sigmoidea), y la fórmula es:

Juntos, obtenemos la función de hipótesis para el modelo de regresión logística:

A continuación, debe escribir código para implementar la función Sigmoid . Después de escribir, intente probar algunos valores. Si xel valor positivo de sigmoid es grande, el valor de la función debe estar cerca de 1; si xel valor negativo de sigmoid es grande, el El valor de la función debe estar cerca de 0. Y para xigual a 0, el valor de la función es 0,5.

Asegúrese de que después de llamar a la función Sigmoid que implementó, el siguiente código generará la siguiente imagen:

###在这里填入代码###
def sigmoid(z):
    
    return 1.0 / (1.0 + np.exp(-z))

###请运行并测试你的代码###
nums = np.arange(-10, 10, step=1)

fig, ax = plt.subplots(figsize=(12,8))
ax.plot(nums, sigmoid(nums), 'r')
plt.show()

1.2.2 Función de costo y gradiente

1.2.2.1 Función de costo

我们知道逻辑回归的代价函数是：
$j\left(yo\right)=\frac{}{metro}\sum _{yo=1}[-y^{\left(yo\right)}iniciarsesión\left(h_{}\left(X^{\left(yo\right)}\right)\right)-\left(1-y^{\left(yo\right)}\right)iniciarsesión\left(1-h_{}\left(X^{\left(yo\right)}\right)\right)]$

Ahora, debe escribir código para implementar la función de costo para calcular el costo de la regresión logística y, después de probar los datos proporcionados, el costo inicial es de aproximadamente 0,693.

Puntos principales :

• Implemente la función de costo, los parámetros son theta, X, y.
• Devuelve el valor del costo calculado.
• Donde theta es un parámetro, X es la columna de características en el conjunto de entrenamiento, y es la columna de etiquetas en el conjunto de entrenamiento y las tres son matrices.

###在这里填入代码###
def cost(theta,X,y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
    return np.sum(first - second) / (len(X)) 

    

###请运行并测试你的代码###
#增加一列值为1，这和我们在练习1中的操作很相似
data.insert(0, 'Ones', 1)

# 定义X为训练数据，y为目的变量
cols = data.shape[1]
X = data.iloc[:,0:cols-1]
y = data.iloc[:,cols-1:cols]

# 将X,y转换为numpy数组，并初始化theta值为0
X = np.array(X.values)
y = np.array(y.values)
theta = np.zeros(3)

cost(theta, X, y)

0.6931471805599453

1.2.2.2 Descenso de gradiente

A continuación, necesitamos escribir código para implementar el descenso de gradiente para calcular nuestros datos de entrenamiento, etiquetas y algunos parámetros θ \thetaGradiente de$\theta$ .

Puntos principales :

• El código implementa la función de gradiente y los parámetros son theta, X, y.
• Devuelve el valor de gradiente calculado.
• Donde theta es un parámetro, X es la columna de características en el conjunto de entrenamiento, y es la columna de etiquetas en el conjunto de entrenamiento y las tres son matrices.

El descenso del gradiente por lotes se transforma en un cálculo vectorizado: $\frac{}{metro}{X}^T\left(Syogramomoyod\right(X\theta )-y)$

$$\frac{\partial J\_(yo}{\partial {\theta }_{}}=\frac{}{metro}\sum _{yo=1}(h_{}\left(X^{\left(yo\right)}\right)-y^{\left(yo\right)})x_{{}_{}}^{(yo}$$

Tenga en cuenta aquí que en realidad no estamos realizando un descenso de gradiente en esta función, solo estamos calculando un paso de gradiente. Como estamos usando Python, podemos usar optimizelos espacios de nombres de SciPy para hacer lo mismo.

###在这里填入代码###
def gradient(theta, X, y):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)

    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)

    error = sigmoid(X * theta.T) - y

    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        grad[i] = np.sum(term) / len(X)

    return grad

    

###请运行并测试你的代码###
gradient(theta, X, y)

array([ -0.1       , -12.00921659, -11.26284221])

1.2.3 Encontrar los parámetros óptimos

Ahora se puede implementar la búsqueda de parámetros óptimos con el newton truncado (TNC) de SciPy.

###请运行并测试你的代码###
import scipy.optimize as opt
result = opt.fmin_tnc(func=cost, x0=theta, fprime=gradient, args=(X, y))
result

(array([-25.16131868,   0.20623159,   0.20147149]), 36, 0)

Veamos el valor de la función de costo bajo esta conclusión:

###请运行并测试你的代码###
cost(result[0], X, y)

0.2034977015894744

1.2.4 Evaluación de la regresión logística

A continuación, necesitamos escribir código para implementar la función de predicción, usando los parámetros óptimos aprendidos $\theta$ para generar resultados de predicción para el conjunto de datosX. Esta función se puede usar para calificar la precisión de entrenamiento del clasificador que definimos.

Función de hipótesis para regresión logística:

$h_{}\left(X\right)=\frac{}{1+{mi}^{-{yo}^{TX}\_}}$
Esta $h_{}$Cuando sea mayor o igual a 0.5, prediga y=1

Esta $h_{}$Cuando sea menor que 0.5, prediga y=0.

Puntos principales :

• El código implementa la función de predicción y los parámetros son theta, X.
• Devuelve el resultado de predicción correspondiente a cada fila de datos en X.
• donde theta es el parámetro y X es la columna de características en el conjunto de entrenamiento.

###在这里填入代码###
def predict(theta, X):
    probability = sigmoid(X * theta.T)
    return [1 if x >= 0.5 else 0 for x in probability]
    

###请运行并测试你的代码###
theta_min = np.matrix(result[0])
predict(theta_min, X)

[0,
 0,
 0,
 1,
 1,
 0,
 1,
 0,
 1,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 0,
 0,
 1,
 1,
 0,
 1,
 0,
 0,
 1,
 1,
 1,
 1,
 0,
 0,
 1,
 1,
 0,
 0,
 0,
 0,
 1,
 1,
 0,
 0,
 1,
 0,
 1,
 1,
 0,
 0,
 1,
 1,
 1,
 1,
 1,
 1,
 1,
 0,
 0,
 0,
 1,
 1,
 1,
 1,
 1,
 0,
 0,
 0,
 0,
 0,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 1,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 0,
 1,
 1,
 1,
 1,
 1,
 0,
 1]

###请运行并测试你的代码###
predictions = predict(theta_min, X)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 89%

2 Regresión logística regularizada

En esta parte del ejercicio, mejoraremos el algoritmo de regresión logística agregando un término de regularización.

La regularización es un término en funciones de costo que hace que un algoritmo favorezca modelos "más simples". Esta teoría ayuda a reducir el sobreajuste y mejorar la capacidad de generalización del modelo.

Imagine que es el supervisor de producción en una fábrica y tiene resultados de prueba para algunos chips en dos pruebas. Para estas dos pruebas, desea decidir si el chip debe ser aceptado o rechazado. Para ayudarlo a tomar esa difícil decisión, tiene un conjunto de datos de prueba de chips anteriores, a partir del cual puede construir un modelo de regresión logística .

2.1 Visualización de datos

Similar al ejercicio de la primera parte, primero visualice los datos:

path =  '/home/jovyan/work/ex2data2.txt'
data2 = pd.read_csv(path, header=None, names=['Test 1', 'Test 2', 'Accepted'])
data2.head()

	Prueba 1	prueba 2	Aceptado
0	0.051267	0.69956	1
1	-0.092742	0.68494	1
2	-0.213710	0.69225	1
3	-0.375000	0.50219	1
4	-0.513250	0.46564	1

positive = data2[data2['Accepted'].isin([1])]
negative = data2[data2['Accepted'].isin([0])]

fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(positive['Test 1'], positive['Test 2'], s=50, c='b', marker='o', label='Accepted')
ax.scatter(negative['Test 1'], negative['Test 2'], s=50, c='r', marker='x', label='Rejected')
ax.legend()
ax.set_xlabel('Test 1 Score')
ax.set_ylabel('Test 2 Score')
plt.show()

Para esta parte de los datos, podemos ver que no existe un límite de decisión lineal obvio entre los puntos de datos de diferentes clases para dividir las dos clases de datos.

Por lo tanto, la regresión logística no puede funcionar bien en este conjunto de datos porque la regresión logística solo conoce límites de decisión lineales.

2.2 Mapeo de características

Una forma de ajustar mejor los datos es construir características derivadas de polinomios de las características originales, conocidas como mapas de características. Como se muestra en la siguiente figura, como resultado de este mapeo, nuestros dos vectores propios $X_{},X_{}$(puntuaciones de dos pruebas de control de calidad) se han transformado en un vector de 28 dimensiones.

Un clasificador de regresión logística entrenado en este vector de características de alta dimensión tendrá un límite de decisión más complejo y exhibirá curvas de partición no lineales cuando se represente en 2D.

Si bien los mapas de características nos permiten construir un clasificador más expresivo, también es más propenso a sobreajustarse. A continuación, debe implementar la regresión logística regularizada para ajustar los datos y usar la regularización para ayudar con el sobreajuste .

¡Comenzamos creando un conjunto de características polinómicas!

# 设定映射深度
degree = 5
# 分别取两次测试的分数
x1 = data2['Test 1']
x2 = data2['Test 2']

data2.insert(3, 'Ones', 1)

# 设定计算方式进行映射
for i in range(1, degree):
    for j in range(0, i):
        data2['F' + str(i) + str(j)] = np.power(x1, i-j) * np.power(x2, j)

# 整理数据列
data2.drop('Test 1', axis=1, inplace=True)
data2.drop('Test 2', axis=1, inplace=True)

print("特征映射后具有特征维数：%d" %data2.shape[1])
data2.head()

特征映射后具有特征维数：12

	Aceptado	Unos	F10	F20	F21	F30	F31	F32	F40	F41	F42	F43
0	1	1	0.051267	0.002628	0.035864	0.000135	0.001839	0.025089	0.000007	0.000094	0.001286	0.017551
1	1	1	-0.092742	0.008601	-0.063523	-0.000798	0.005891	-0.043509	0.000074	-0.000546	0.004035	-0.029801
2	1	1	-0.213710	0.045672	-0.147941	-0.009761	0.031616	-0.102412	0.002086	-0.006757	0.021886	-0.070895
3	1	1	-0.375000	0.140625	-0.188321	-0.052734	0.070620	-0.094573	0.019775	-0.026483	0.035465	-0.047494
4	1	1	-0.513250	0.263426	-0.238990	-0.135203	0.122661	-0.111283	0.069393	-0.062956	0.057116	-0.051818

2.3 Función de costo y gradiente

A continuación, debe escribir código para calcular la función de costo y el gradiente de la regresión logística regularizada, y devolver el valor de costo y el gradiente calculados .

正则化逻辑回归的代价函数如下：
$$j\left(yo\right)=\frac{}{metro}\sum _{yo=1}[-y^{\left(yo\right)}iniciarsesión\left(h_{}\left(X^{\left(yo\right)}\right)\right)-\left(1-y^{\left(yo\right)}\right)iniciarsesión\left(1-h_{}\left(X^{\left(yo\right)}\right)\right)]+\frac{}{2metros}\sum _{j=1}{i}_j^{}$$

donde $\lambda$ es el parámetro de "tasa de aprendizaje" cuyo valor afecta el valor del término de regularización en la función. Y no debería regularizar el parámetro$i_{}$。

###在这里填入代码###
def costReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
    second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
    reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2))
    return np.sum(first - second) / len(X) + reg 

    

A continuación, debemos implementar una función de gradiente regularizada que minimice la función de costo mediante el descenso de gradiente.

Porque en el cálculo de la función de costo no tenemos $i_{}$Regularización, por lo que el algoritmo de descenso de gradiente se dividirá en dos casos:

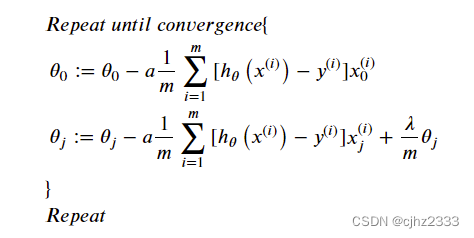
Ajuste la fórmula de actualización cuando j=1,2,…,n en el algoritmo anterior:
$i_{}:=i_{}(1-a\frac{}{metro})-a\frac{}{metro}\sum _{yo=1}(h_{}\left(X^{\left(yo\right)}\right)-y^{\left(yo\right)})x_j^{(yo}$

###在这里填入代码###
def gradientReg(theta, X, y, learningRate):
    theta = np.matrix(theta)
    X = np.matrix(X)
    y = np.matrix(y)
    
    parameters = int(theta.ravel().shape[1])
    grad = np.zeros(parameters)
    
    error = sigmoid(X * theta.T) - y
    
    for i in range(parameters):
        term = np.multiply(error, X[:,i])
        
        if (i == 0):
            grad[i] = np.sum(term) / len(X)
        else:
            grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:,i])
    
    return grad

    

A continuación, inicialice variables similares a los ejercicios de la primera parte.

# 从数据集中取得对应的特征列和标签列
cols = data2.shape[1]
X2 = data2.iloc[:,1:cols]
y2 = data2.iloc[:,0:1]

# 转换为Numpy数组并初始化theta为零矩阵
X2 = np.array(X2.values)
y2 = np.array(y2.values)
theta2 = np.zeros(11)

# 设置初始学习率为1，后续可以修改
learningRate = 1

A continuación, pruebe su implementación de las funciones de costo y gradiente usando los valores de las variables inicializadas.

###请运行并测试你的代码###
costReg(theta2, X2, y2, learningRate)

0.6931471805599454

###请运行并测试你的代码###
gradientReg(theta2, X2, y2, learningRate)

array([0.00847458, 0.01878809, 0.05034464, 0.01150133, 0.01835599,
       0.00732393, 0.00819244, 0.03934862, 0.00223924, 0.01286005,
       0.00309594])

2.4 Encuentra los parámetros óptimos

Ahora podemos usar la misma función de optimización que en la primera parte para calcular el resultado optimizado.

result2 = opt.fmin_tnc(func=costReg, x0=theta2, fprime=gradientReg, args=(X2, y2, learningRate))
result2

(array([ 0.53010246,  0.29075567, -1.60725764, -0.58213819,  0.01781027,
        -0.21329507, -0.40024142, -1.3714414 ,  0.02264304, -0.95033581,
         0.0344085 ]), 22, 1)

2.5 Evaluación de la regresión logística regularizada

Finalmente, podemos usar la función de predicción de la Parte 1 para ver qué tan preciso es nuestro esquema en los datos de entrenamiento.

theta_min = np.matrix(result2[0])
predictions = predict(theta_min, X2)
correct = [1 if ((a == 1 and b == 1) or (a == 0 and b == 0)) else 0 for (a, b) in zip(predictions, y2)]
accuracy = (sum(map(int, correct)) % len(correct))
print ('accuracy = {0}%'.format(accuracy))

accuracy = 78%