El concepto de gráfico: la estructura de datos de un gráfico consta de dos conjuntos, uno es el conjunto de vértices V (vértice) y el otro es el conjunto de aristas E (Borde); los gráficos no dirigidos generalmente se registran como G(V , E ); los gráficos dirigidos se registran como G<V, E>
Un gráfico dirigido significa que la dirección del borde se distingue por la dirección, por ejemplo, de A->B; de A a B, pero B no puede llegar a A (el borde del gráfico dirigido es una flecha, llamada arco, y la cabeza del arco es w, la cola del arco es v)
Los bordes de un gráfico no dirigido no tienen distinción de dirección, siempre que AB, puede ir de A a B, y de B a A
Los conceptos importantes son los siguientes:
1: El gráfico no debe ser un gráfico vacío, es decir, el conjunto de vértices no debe estar vacío, y el conjunto de aristas puede estar vacío
2: Gráfico completo: si hay una arista entre dos vértices cualesquiera (nótese que la arista aquí hay dos vértices conectados directamente entre sí), entonces se dice que el gráfico está completo.
Un grafo completo no dirigido tiene n*(n-1)/2 aristas.
Un grafo completo dirigido tiene n*(n-1) aristas
3: Subgrafo: Un nuevo grafo compuesto por cierta parte de los vértices en el grafo y una parte de los aristas conectados a los vértices es el subgrafo. (Tenga en cuenta que no debe decir simplemente "un subconjunto de aristas" y "un subconjunto de vértices", deben ser las aristas conectadas a los vértices para formar un subgrafo)
Para gráficos no dirigidos, los conceptos súper importantes son:
4: Conectado: si hay un camino desde el vértice A al vértice B, entonces se dice que AB es conexo
5: Gráfico conexo y gráfico no conexo: si dos vértices cualesquiera en el gráfico tienen caminos (no necesariamente caminos directamente conectados, Nota aquí que se distingue del concepto de grafo completo), el grafo se llama grafo conexo, que literalmente significa "todo el grafo es conexo", si algunos vértices no están conectados con otros vértices, es decir, algunos vértices están aislados , se llama un gráfico desconectado.
6: Componente conexa (también llamada subgrafo máximamente conexo): Si hay ABC conexo y DE conexo en un grafo G, se dice que tiene dos componentes conexos, es decir, dos subgrafos máximamente conexos (es decir, en el grafo G, , un subgrafo conexo).
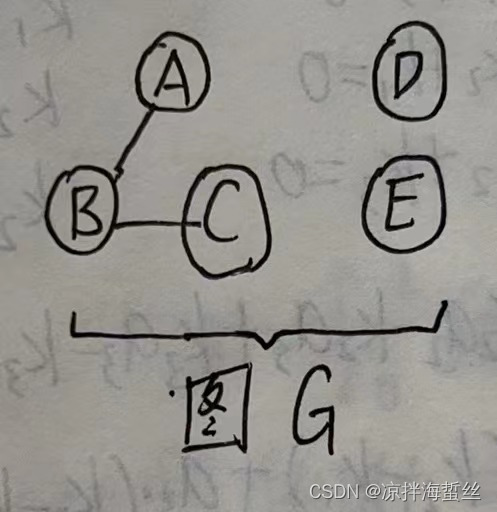
(7) Para un gráfico no dirigido, N vértices necesitan al menos N-1 aristas para formar un gráfico conectado (el dibujo es fácil de entender), si N vértices necesitan formar un gráfico completo, al menos n*(n-1) es requerido /2 lados.
Si el número de aristas es menor que n-1, el gráfico debe desconectarse.
Para grafos dirigidos, los conceptos súper importantes son:
8: Conectividad fuerte: Este concepto debe distinguirse de la conectividad de los gráficos no dirigidos, porque los gráficos dirigidos son dirigidos, por lo que su conectividad debe ser una conectividad "más fuerte", así que recuerda la conectividad fuerte. Si AB está fuertemente conectado, debe haber A->B y A<- B; es decir, ambas direcciones deben existir para que se llame conectividad fuerte.
9: Grafo fuertemente conexo: si en el grafo dirigido G, dos vértices cualesquiera del grafo tienen un camino (no se requiere un camino de conexión directa, pueden pasar N vértices, siempre que haya un camino), entonces el grafo G es un grafo fuertemente conexo
10: Componente fuertemente conexo (también llamado subgrafo extremadamente fuertemente conexo): Debe distinguirse del concepto de componente conexo en un grafo no dirigido.Componente fuertemente conexo significa que debe haber un ciclo en el subgrafo, por lo que es juzgado si hay un fuerte componente conexo en un gráfico dirigido. Para componentes conexos, debemos encontrar un bucle. Si no hay bucle, prueba que el último vértice D no se puede rastrear hasta el primer vértice A, es decir, no no hay camino de D a A, entonces no está fuertemente conectado.
11: Para un grafo dirigido, un grafo dirigido con N vértices requiere al menos n aristas (formando un anillo) para formar un grafo fuertemente conectado. Para formar un gráfico completo dirigido (un gráfico completo dirigido debe ser un gráfico fuertemente conectado, y cualquier vértice tiene dos trayectorias de flecha hacia adelante y hacia atrás), se requieren n*(n-1) aristas.
Subgrafos máximamente conectados y subgrafos mínimamente conectados:
12: Son todos para grafos no dirigidos, la diferencia entre máximo y mínimo es que el máximo debe contener todas las aristas del subgrafo, es decir, no solo debe ser conexo, sino también conservar todas las aristas. Los subgrafos conectados mínimos solo necesitan mantener el número mínimo de aristas para garantizar que el gráfico esté conectado, es decir, que se pueda conectar.
Nota ⚠️: el árbol de expansión es un subgrafo mínimamente conectado, pero el árbol de expansión no es un subgrafo de conexión máxima (porque no contiene todos los bordes), por lo que, por supuesto, el árbol de expansión no es un componente conectado
Gráficos densos y dispersos:
13: La densidad y la escasez son para los bordes. El número de bordes es denso y el número de bordes es escaso. (Imagínalo como una red de pesca. Si hay muchos lados, toda la red será muy densa; si hay pocos lados, toda la red será muy escasa)
Ejemplos de gráficos:
(1) Un gráfico no dirigido con N vértices y N aristas debe tener un ciclo (al dibujar el gráfico se puede encontrar que si cada vértice tiene una arista, debe haber un ciclo); pero tenga en cuenta que un ciclo no es necesariamente conexo. Depende del número de aristas (si un grafo no dirigido con n nodos tiene n*(n-1)/2 aristas, debe ser un grafo completo, y el grafo completo debe ser conexo y tener un ciclo) y de un cierto vértice Ya sea que se realice una búsqueda profunda o una búsqueda amplia, se puede recorrer todo el gráfico.
(2) El recorrido del gráfico no es simplemente partir de un cierto vértice y recorrer el resto de los vértices. Debido a que el gráfico puede ser desconectado, a partir de un cierto vértice, solo se puede atravesar un cierto subgráfico, y los vértices en los otros subgráficos no se pueden atravesar, por lo que para atravesar el gráfico, el conjunto de vértices V debe recorrerse y el conjunto de vértices V debe atravesarse. los vértices están marcados con Si todavía hay algunos vértices que no han sido marcados con marcas transversales después de completar un recorrido, el siguiente ciclo comenzará hasta que todos los vértices del conjunto de vértices V estén marcados con marcas transversales (los vértices en el subgrafo en este el tiempo también se ha marcado transversal) se considera un gráfico transversal completo.
(3) Un grafo no dirigido no conectado con 28 aristas tiene al menos () vértices
Análisis: Hay 28 aristas que no están conectadas, y se requiere el número mínimo de vértices. Si el número de vértices es el menor, y el número de aristas se consume, entonces debe ser completa Para este hijo pródigo, veamos cuántos grafos completos no dirigidos se pueden formar con 28 aristas, y sustituimos la fórmula: N*(N-1) / 2 = 28, la solución es N = 8; 8 vértices están formados por 28 aristas Se crea un grafo completamente no dirigido, pero el tópico no está conectado, luego se agrega un vértice aislado, 9 vértices son suficientes. Hay muchos temas similares, pero todos tienen que ver con la fórmula del número de aristas del gráfico completo del gráfico dirigido y no dirigido.
(4) [2010] Si hay 7 vértices en el grafo no dirigido G(V , E), para asegurar que el grafo G sea conexo en todo caso, se necesitan al menos (16) aristas porque tiene 7 vértices, y
To asegúrese de que cualquier situación sea conexa, solo puede ver cuántas aristas agrega, y al agregar otra arista debe estar conectada, es decir, primero deje que sus 6 vértices formen un gráfico completo no dirigido, consumiendo 6 * (6-1) / 2 = 15 aristas, entonces + 1 = 16, por lo que debe estar conectado al séptimo vértice. De esta forma, se debe garantizar que el grafo G sea un grafo conexo. Debido a que 15 aristas ya han llenado 6 vértices, no tienen lugar para agregar otra arista, y solo pueden tener una relación con el séptimo vértice. Una vez que ocurre una relación, se formará inmediatamente un gráfico conectado.
Para un grafo no dirigido con 6 vértices , cuando hay () aristas, se puede garantizar que sea un grafo conexo
(5) El grafo G tiene n vértices, si es un grafo no dirigido conexo, el número de aristas es al menos:
Según la fórmula, siempre que la conectividad esté garantizada, un grafo no dirigido de n vértices solo necesita n-1 aristas
Si es un grafo dirigido fuertemente conectado, el número de aristas es al menos:
De acuerdo con la fórmula, para asegurar una fuerte conectividad, n vértices deben usar n aristas para rodear un anillo
(6) El grafo no dirigido G tiene 23 aristas, 5 vértices de grado 4, 4 vértices de grado 3 y el resto son vértices de grado 2. ¿Cuántos vértices tiene el grafo G en total?
Análisis:
Una arista puede aportar dos grados, entonces hay 46 grados en total, y 5 vértices con grado 4 consumen 20 grados; 4 vértices con grado 3 consumen 12 grados; los 46 restantes - 12- 20 = 14; el título dice que el resto son de grado 2, entonces 14/2 = 7, es decir, hay 7 vértices de grado 2, y el grafo G tiene un total de 7 + 5 + 4 = 16 vértices
(7) Si un grafo no dirigido con n vértices y e aristas es un bosque, entonces el bosque debe tener () árboles
. Un ejemplo extremo pero razonable (por ejemplo, un árbol con un grado de 3, tiene 10086 nodos, pregunte la profundidad y la altura del árbol, use directamente 10083 como el número de pilas de nodos, y los últimos 3 como el ejemplo pervertido de nodos de hoja) Idea 1
: Aquí asumimos que hay x árboles en el bosque, entonces necesito usar x- 1 aristas para formar un nuevo árbol, pero hay e aristas en los x árboles originales, por lo que el nuevo árbol tiene un total de Hay x-1+e aristas. De acuerdo con la naturaleza del árbol, excepto que el nodo raíz no tiene ninguna arista conectada, todos los demás nodos tienen al menos una arista que apunta hacia él, por lo que el número de puntos de resumen = número total de aristas + 1 es n = (
x- 1+e) + 1
x = ne
Idea 2: Por ejemplo, si asumo que cada una de las aristas e está conectada a dos vértices para formar un árbol, entonces 2e vértices se consumen para formar un árbol e, y los vértices restantes forman un árbol único sin El árbol de borde, es decir, el resto: n - 2e vértices, un total de n - 2e árboles,
entonces hay un total de: n-2e+e = n - e árboles
(8) [2017] El gráfico G no dirigido conocido contiene 16 aristas, 3 vértices con grado 4, 4 vértices con grado 3 y otros vértices con grado menor que 3, luego los vértices contenidos en el gráfico G El número es al menos ()
análisis :
16 lados dedican 32 grados, el grado 4 tiene 3, consume 12 grados; el grado 3 tiene 4, consume 12 grados; luego el resto: 32 - 12 -12 = 8 grados; restante Puede haber
vértices con grado 1 y 2 , pero la cantidad de vértices incluidos en el tema debe ser al menos, es decir, la cantidad mínima de vértices permitidos, entonces debo elegir un grado de 2, tal vértice consume 2 grados, y puede consumir el restante lo antes posible grados 8/2 = 4, es decir, solo se necesitan 4 vértices más de grado 2.
Entonces hay vértices totales:
3 + 4 + 4 = 11
almacenamiento de gráficos
Método de matriz de adyacencia (adecuado para gráficos densos):
typedef struct {
char v[100];
int e[100][100];
} Graph;
Cuando el método de matriz de adyacencia almacena un grafo no dirigido, debe ser una matriz simétrica, porque no distingue entre en grado y en grado. Como es una matriz simétrica, admite almacenamiento comprimido, es decir, solo la parte superior o superior. parte triangular inferior se almacena, por lo que en la densa En la aplicación del gráfico, tiene muy buen efecto.
Su método de almacenamiento específico es el siguiente:
Para un gráfico no dirigido con 4 vértices
(1) suponiendo que hay vértices ABCD, se genera una matriz cuadrada de 4*4, y las filas y columnas son ABCD, y luego secuencialmente desde la primera fila a la primera Una columna comienza con 01 (con lado 1, sin lado 0)
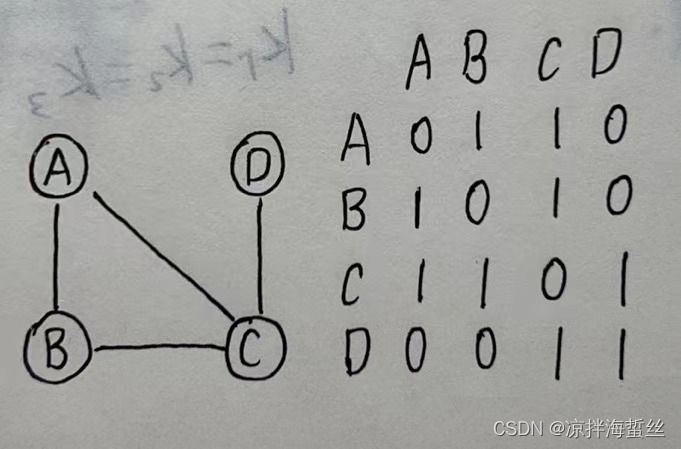
Dado que el número de esta matriz es 1, representa cuántas rutas hay de un punto determinado a un punto determinado con una longitud de camino de 1. Entonces se puede ver claramente que de A a La longitud de A es cero, A a B y B a C.
(2) Si la matriz se multiplica por sí misma, se obtiene el cuadrado de la matriz El grado cuadrado es 2, lo que significa desde un cierto punto hasta En cierto punto, ¿cuántas rutas hay con una longitud de camino de 2:

Por ejemplo, reflejado en la matriz, hay 2 rutas de A a A con un camino longitud de 2, que son [A] y [B] (la primera fila de la matriz de la izquierda Dos columnas) multiplicado por 【B】【A】(la primera fila de la segunda columna de la matriz de la derecha) +【A 】【C】 multiplicado por 【C】【A】 = 2. También quiere decir que estas dos rutas son: de A a B, y luego de B a A; o de A a C, y luego de C a A; es increíble, pon otro
ejemplo: la nueva matriz de C a Hay 3 rutas con una longitud de camino de 2 en C, que son:
【C】【A】multiplicado por 【A】【C】 + 【C】【B】multiplicado por 【B】【C】 + 【C】【D】 Multiplicado por 【D】【C】 = 3
Es decir, de C a A y luego de A nuevamente a C,
de C a B y luego de B nuevamente a C,
de C a D y luego de D nuevamente a C
combinar perfectamente la ruta y la ruta Se muestran los números.
(3) Si el cuadrado se multiplica por sí mismo para formar una matriz cúbica, representa cuántas rutas hay de cierto punto a cierto punto con una longitud de camino de 3, y cómo ir, quedará claro:
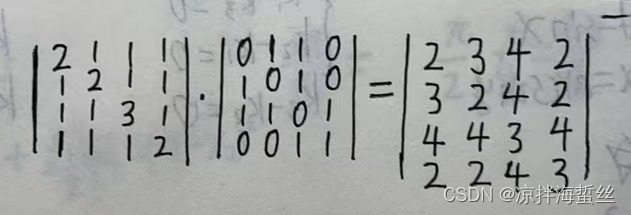
Con base en la longitud de camino de 2, hay 4 rutas de A a C con una longitud de camino de 3, que son:
(1) 【A】【A】multiplicado por 【A】【C】 + (2) 【A】【B】multiplicado por 【B】【C】 + (3) 【A】【D】multiplicado por 【D】 [C] = 4
La matriz de la izquierda se obtiene a base de cuadrados, por lo que debemos mirar la hoja de ruta cuando volvamos a los cuadrados:
representa 4 caminos con una longitud de 3:
(1)
donde [A] [ A] es una matriz El camino generado al elevar al cuadrado【A】【B】multiplicado por 【B】【A】+【A】【C】multiplicado por 【C】【A】 = 2 de A a B, luego de B de vuelta a A, y luego
de A a C
, de A a C, luego de C de regreso a A, y luego de A a C
(2)
[A] [B] es el camino generado cuando la matriz se eleva al cuadrado [ A] [C] multiplicado por [C] [ B] = 1
de A a C, luego de C a B, y luego de B a C
(3)
[A] [D] es el camino generado cuando la matriz es [A] [C] al cuadrado multiplicado por [C] [D] = 1
de A a C, luego de C a D, y finalmente de D de regreso a C
Aunque parezca una tontería dar vueltas así, sí puede indicarnos que un camino lleva de un punto determinado a un punto determinado. Si no quieres volver atrás, puedes añadir otra lógica de negocio para filtrarlo. Este efecto sigue siendo muy potente.
Una matriz de adyacencia almacena un gráfico dirigido:
El grafo dirigido usa 1 para representar el grado de salida, lo que significa que el subíndice correspondiente del grafo de salida es 1, y el grado de entrada es 0 (es fácil de entender, porque aquí 1 significa que este camino es transitable, y el de entrada es 0). El grado del gráfico dirigido es para el vértice actual Es intransitable, lo que equivale a que no haya camino, por lo que es 0, solo el grado de salida es transitable, que es 1) aquí también se refiere
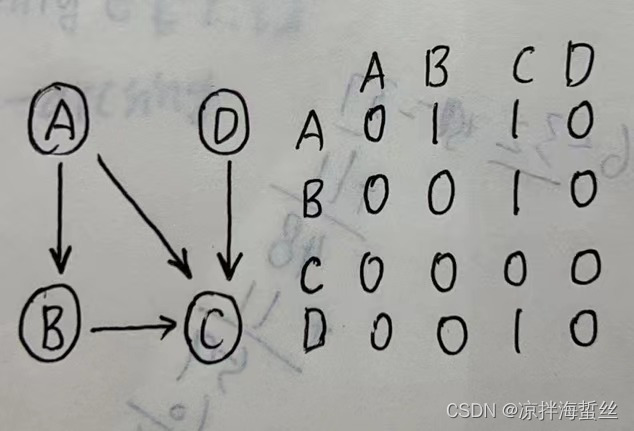
a la longitud del camino de 1, si lo desea para ver la longitud del camino de 2, también puedes hacer esto El cuadrado de la matriz es el mismo que el gráfico no dirigido
Ventajas:
Codificación intuitiva, conveniente y simple, fácil de implementar.
Si es para almacenar un gráfico denso, si es un gráfico no dirigido combinado con el método de compresión de convertir la matriz triangular superior e inferior en una matriz unidimensional, puede ahorrar mucho espacio.
Desventajas:
la eficiencia es relativamente baja, la cantidad de cálculo es grande y el almacenamiento de resultados intermedios ocupará mucho espacio en la memoria.
Dado que la matriz está fijada para ser una matriz cuadrada de n*n, si se trata de un gráfico disperso, se generará una gran cantidad de espacio de almacenamiento vacío innecesario.
Si desea eliminar un nodo en la matriz de adyacencia, debe atravesar, complejidad de tiempo O (n)
método de lista de adyacencia
Para almacenar matrices dispersas de manera más eficiente y conveniente, existe un método de lista de adyacencia, que utiliza el método de almacenamiento de matriz + lista enlazada (similar a una tabla hash), asigna una posición de subíndice de matriz a cada vértice y, al mismo tiempo, asigna la posición del subíndice del arreglo conectado al vértice Los subíndices del arreglo de los vértices están vinculados detrás de los nodos.
// 边表结点
typedef struct ArcNode{
int index; // 该边指向的顶点的数组下标
struct ArcNode *next; //下一个边表结点的指针
} ArcNode;
// 顶点表结点
typedef struct VNode{
char data; // 顶点信息,存储例如:ABCD,1234之类的值
ArcNode *next; // 链接第一个边表结点
} AdjList[100];
// 邻接表结构
typedef struct {
AdjList[100];
int vexnum; arcnum; // 顶点数和弧数
} ALGraph
Si es un grafo no dirigido, existirá una arista en dos nodos de la tabla de aristas al mismo tiempo; si es para un grafo dirigido, solo se registrará la arista, y sólo existirá una arista en un nodo de la tabla de aristas (esta figura se toma de
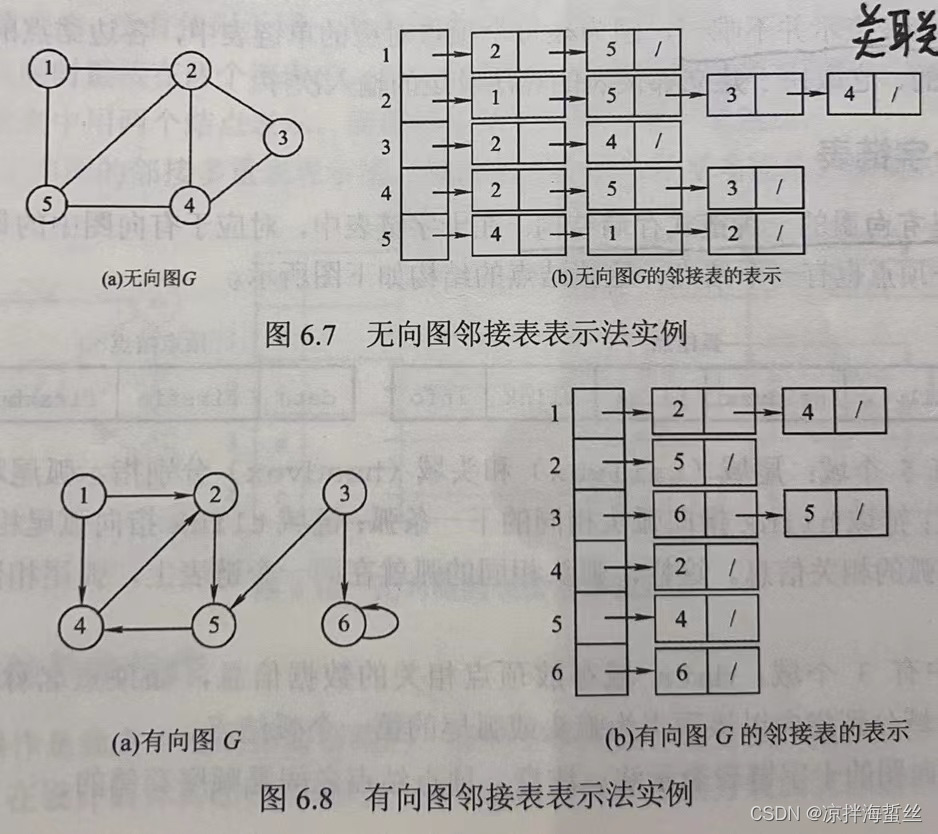
la estructura de datos de Wangdao)
Si la lista de adyacencia se usa para almacenar el gráfico no dirigido, entonces debe haber un número par de nodos de la tabla de bordes; si es un número impar de nodos de la tabla de bordes, entonces debe ser un gráfico dirigido.
Ejemplo:
(1) La lista de adyacencia de un grafo no dirigido con n vértices tiene como máximo (n*(n-1)) nodos de la lista de aristas Análisis
: Para un grafo no dirigido con n vértices, si es un grafo completo, tiene el la mayoría de los bordes, hay como máximo n*(n-1)/2 bordes, y cada borde generará dos nodos de tabla de bordes, por lo que habrá como máximo n*(n-1) nodos de tabla de bordes.
(2) Suponiendo que hay n vértices y el gráfico dirigido de e aristas está representado por una lista de adyacencia, la complejidad temporal de eliminar todas las aristas relacionadas con un cierto vértice v es: O(n+e) Análisis: Para eliminar
un
determinado Para todos los bordes del vértice, es necesario recorrer para encontrar el vértice v correspondiente, y luego eliminar su tabla de bordes salientes a su vez. En este momento, todos los bordes salientes del vértice v se eliminan, porque hay en la mayoría de las n-1 tablas de aristas salientes, es decir, asumiendo que v tiene aristas salientes para todos los demás vértices
. En el ciclo anterior, se deben eliminar sus aristas entrantes. Para eliminar aristas entrantes, primero recorra los nodos O(n) de la tabla de vértices, y encuentre las tablas de borde salientes de los nodos de la tabla de vértices, una por una, excepto V. Enlace O (e), elimine el borde saliente relacionado con V, de modo que el borde entrante de V también desaparezca, la complejidad total es O (n +
e )
(3) [2021] Se sabe que un grafo conexo no dirigido G está compuesto por un conjunto de vértices V y un conjunto de aristas E, |E|>0, cuando el número de vértices de grado impar en G es un número par no mayor que 2, G contiene Todos los caminos con una longitud de |E| (llamados EL) caminos (el gráfico G se almacena en una matriz de adyacencia) (1)
Diseñe un algoritmo para juzgar si hay un camino EL en G, si existe , devuelve 1, de lo contrario devuelve 0; dale al algoritmo La idea básica
(a decir verdad, en ese momento vi lo que el título describía en ese momento. El número de vértices con un grado impar y un número par no mayor que 2 incluía la ruta EL. Esta sección ha estado atascada durante mucho tiempo y no quería entenderlo. También es después de leer el análisis que sabemos que solo necesitamos contar la cantidad de vértices con un número impar, y vea si es 0 o 2, independientemente de la ruta EL de la pluma) Dado que uso la matriz de adyacencia, solo necesito comenzar el bucle externo
desde Atravesando desde la primera línea hasta la última línea, el bucle de memoria atraviesa desde la primera columna hasta la última columna, cada línea es la información del grado de entrada y salida de un vértice, si es 1, entonces ++, y finalmente usa su grado para juzgar si %2=0, si es así, prueba que el vértice actual es par , si no, prueba que el grado del vértice actual es impar, suma de vértice impar++;
finalmente comprueba si la suma es 0 o 2, si es así, hay un camino EL, si no, no lo hay.
(2) Código
(3) Explique la complejidad temporal y espacial del algoritmo diseñado
Dado que la matriz de adyacencia es una matriz cuadrada de n*n, el costo del ciclo es O(n^2); la complejidad espacial es O(1)
Gráfico de recorrido:
BFS de profundidad primero (concéntrese en un camino hasta el final, cuando no haya camino por recorrer, y luego regrese y elija otro camino)
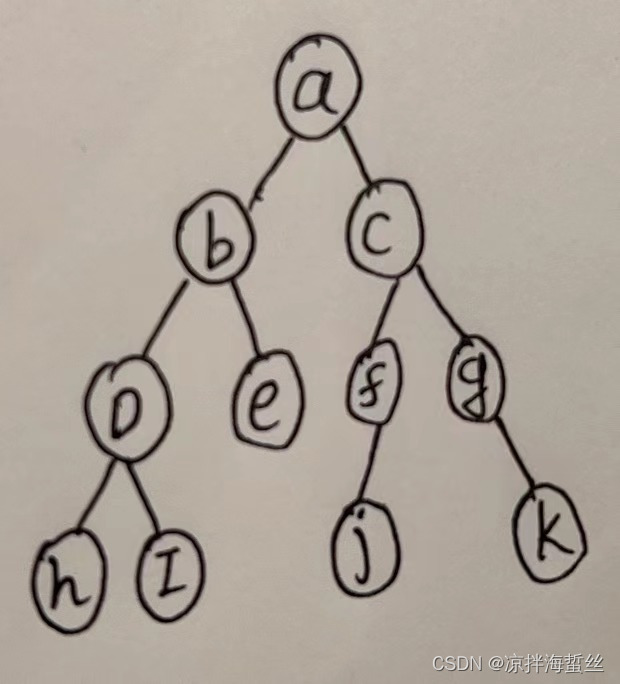
Proceso:
Inicializar una cola auxiliar
(1) Suponiendo que comenzando desde el nodo raíz a, hay nodos b y c conectados, primero coloque a en la cola, luego coloque a fuera de la cola y luego coloque b, c en el cola (2) b
fuera Equipo, poner de cerca de b en el equipo; c fuera del equipo, poner fg cerca de c en el equipo
(3) d fuera, hola dentro, e fuera, nada en el equipo, f fuera, j in, g Fuera del equipo, k dentro del equipo
(4) hola fuera del equipo, jk fuera del equipo
(5) se completa la búsqueda de profundidad
Debido al uso de una matriz auxiliar, el tamaño generalmente se establece en el número de vértices, y la complejidad del espacio es O(V)
cuando se usa el almacenamiento de la lista de adyacencia. Tiempo: al
buscar el punto de conexión del vértice, está tanteando a lo largo del borde, por lo que cada borde debe atravesar un lado, y la complejidad del tiempo es O(E).Cuando
se usa el almacenamiento de matriz de adyacencia:
debido a la matriz cuadrada de N*N vértices, la complejidad del tiempo es O(V^2) veces
Se puede generar un árbol de acuerdo con el ancho primero, llamado árbol de expansión primero el ancho, pero el árbol de expansión primero el ancho no es único
SFD primero en amplitud (de cerca a lejos, cada paso en cada dirección)
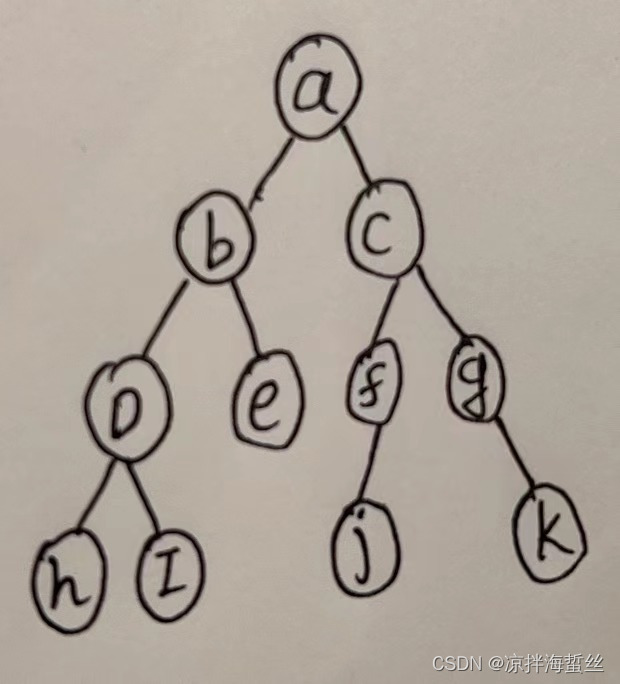
La búsqueda en profundidad generalmente se lleva a cabo recursivamente
(1) comienza desde a, primero encuentra b, b a d, d a h, el primer camino llega a su fin, regresa a d (
2) d a i, el segundo camino también termina Sí , regresa a d, d encuentra que se ha pasado este camino, regresa a b
(3) b a e, al final, regresa a b, b encuentra que se ha pasado el camino, regresa a a
(4) a a c . . . . . .
(5) Continúe con los pasos 1 a 4 hasta que desaparezcan todos los caminos. Esta es la búsqueda en profundidad.
Cuántos vértices hay, cuántas veces recurre y la pila de trabajo recursiva utilizada para la recursión, por lo que la complejidad del espacio es O (V)
Cuando se usa almacenamiento de lista de adyacencia:
la complejidad de tiempo es O(V + E);
cuando se usa almacenamiento de matriz de adyacencia:
debido a la matriz cuadrada de N*N vértices, la complejidad de tiempo es O(V^2) veces