contenido
1. Búsqueda de compresión de características
En segundo lugar, el problema de la cubierta del dominó cuadrado
3. Genera todas las formas de dominó
3. Búsqueda de compresión de funciones para cubrir problemas
1. Búsqueda de compresión de características
Tome una pregunta simple como ejemplo.
Hay 4 ramas del partido con 20 personas, 20 personas, 10 personas y 10 personas respectivamente.
Ahora tenemos que organizar 30 personas para ver una película en el Cine A y 30 personas para ir al Cine B a ver una película, pero las personas de la misma rama del partido deben estar en el mismo cine.
El número de asiento de cada teatro está numerado del 1 al 30. Las personas de estas 4 ramas del partido son de 10 grupos de proyectos, y la relación correspondiente es balabala, omitida.
Pregunta 1: Para que el número de personas en cada grupo de proyecto sea lo más cercano posible, el método de evaluación es la función de pérdida f = balabala, que se omite. ¿Cómo debe organizarse?
Pregunta 2: Para permitir que todos se sienten con personas de otros grupos de proyectos tanto como sea posible, el método de evaluación es la función de pérdida g = balabala, que se omite. ¿Cómo debe organizarse?
Dado que este problema es muy simple, el primer paso es, obviamente, cómo organizar la correspondencia entre la rama del partido y el teatro.Hay 4 correspondencias en esta pregunta.
Luego, el segundo paso es buscar la solución óptima en función de cada correspondencia.
Si el problema se vuelve, hay 100 ramas del partido, cada una con 3-5 personas, entonces el primer paso es menos obvio, pero en realidad es mejor que el método más violento.
Probablemente el método de búsqueda de fuerza bruta sea enumerar cada permutación de todos y tomar la mejor solución.
Más cerca de casa, para este problema de búsqueda, extraemos una característica para simplificar el problema en un subproblema, y el espacio de solución del subproblema es la degradación del espacio de solución del problema original, luego primero buscamos el solución del subproblema, que es equivalente a hacer el problema original como Para la poda, la mayoría de los casos se suelen cortar .
En segundo lugar, el problema de la cubierta del dominó cuadrado
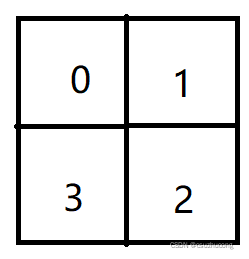
Hay varios dominós cuadrados, cada uno de los cuales tiene un número natural, y los dominós se pueden rotar. Se requiere colocar estos dominós de manera que el número total de los cuatro cuadrados sea igual al número dado.
En general, hay dos tipos de tales problemas, la mayoría de los cuales se pueden revertir y algunos que no se pueden revertir.
1. Minimización digital
Si cada número es mayor que 0, resta un número de los cuatro cuadrados y resta este número del total.
Entonces, el problema se puede transformar en, al menos uno de cada cuadrícula es 0, y los tres restantes son números naturales.
Si los 4 cuadrados son 0, entonces este dominó no necesita participar en el cálculo.
De lo contrario, las cuatro situaciones obtenidas por esta rotación de dominó deben ser diferentes.
2. Si se puede voltear
Para algunas fichas de dominó, es lo mismo si se pueden voltear o no. La forma de juzgar es ver si las fichas de dominó son simétricas. Hay cuatro casos en los que el eje de simetría tiene cuatro líneas.
bool needOverturn(vector<int> v)
{
if (v[0] == v[1] && v[2] == v[3])return false;
if (v[1] == v[2] && v[0] == v[3])return false;
return v[0] != v[2] && v[1] != v[3];
}3. Genera todas las formas de dominó
Si se puede voltear, entonces hay 8 formas para fichas de dominó volteables y 4 formas para otras fichas de dominó.
Si no se puede voltear, solo hay 4 formas.
vector<vector<int>> overturn(vector<int> v)
{
vector<vector<int>> ans(0);
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
if (!needOverturn(v))return ans;
v[0] ^= v[2] ^= v[0] ^= v[2];
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
}4. Resuelve
Código completo:
#include<iostream>
#include <vector>
using namespace std;
vector<vector<int>>num =
{
{2,2,1,0},
{2,2,1,0},
{2,2,1,0},
{2,2,1,0},
{1,0,0,0},
{1,0,0,0},
{2,2,0,0},
{3,1,0,1},
{2,1,0,1},
};
vector<int> s = { 10,9,7,9 };
const bool canOverturn = true;
bool needOverturn(vector<int> v)
{
if (v[0] == v[1] && v[2] == v[3])return false;
if (v[1] == v[2] && v[0] == v[3])return false;
return v[0] != v[2] && v[1] != v[3];
}
vector<vector<int>> overturn(vector<int> v)
{
vector<vector<int>> ans(0);
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
if (!needOverturn(v) || !canOverturn)return ans;
v[0] ^= v[2] ^= v[0] ^= v[2];
for (int i = 0; i < 4; i++) {
ans.push_back(v);
v.push_back(v[0]);
v.erase(v.begin());
}
return ans;
}
bool ok(const vector<vector<int>> &v)
{
for (int i = 0; i < s.size(); i++)
{
int k = s[i];
for (auto& vi : v)k -= vi[i];
if (k)return false;
}
return true;
}
void out(vector<int>v)
{
for (auto& vi : v)cout << vi << " ";
cout << endl;
}
void out(vector<vector<int>>v)
{
for (auto& vi : v)out(vi);
cout << endl << endl;
}
int main()
{
vector<vector<vector<int>>> dom(0);
for (auto &vi : num)dom.push_back(overturn(vi));
int s = 1;
for (auto& vi : dom)s *= vi.size();
cout << s;
int ansnum = 0;
for (int i = 0; i < s; i++)
{
vector<vector<int>>vd;
int k = i;
for (int j = dom.size() - 1; j >= 0; j--)
{
vd.push_back(dom[j][k % dom[j].size()]);
k /= dom[j].size();
}
if (ok(vd)) {
//out(vd);
ansnum++;
if (ansnum % 100 == 0)cout << ansnum << " ";
}
}
cout << ansnum;
return 0;
}El espacio de solución es 4194304 y hay 26412 condiciones satisfactorias.
Si canOverturn = false, el espacio de soluciones tiene 262144 y hay 1642 soluciones que satisfacen la condición.
3. Búsqueda de compresión de funciones para cubrir problemas

1, la representación del dominó
Si hay una cuadrícula, es 1, y si está vacía, es 0
vector<vector<int>> block[] =
{
{
{1,1,1,1}
},
{
{1,0,1},
{1,1,1}
},
{
{1,1,0},
{0,1,0},
{0,1,1}
},
{
{1,1,0},
{1,1,1}
},
{
{1,0,0,0},
{1,1,1,1}
},
{
{1,0,0},
{1,1,1}
},
{
{0,1,0},
{0,1,0},
{1,1,1}
},
{
{1,1,0,0},
{0,1,1,1}
},
{
{1,0,0},
{1,0,0},
{1,1,1}
},
{
{1,1,0},
{0,1,1}
}
};2. Genera todas las formas de dominó
Los dominós ordinarios se pueden girar cuatro veces, mientras que los dominós centrosimétricos solo necesitan girarse dos veces.
Algunas fichas de dominó deben voltearse y otras no (simetría de izquierda a derecha o de arriba a abajo).
Por lo tanto, diferentes fichas de dominó pueden tener 1, 2, 4 y 8 formas diferentes.
Dado que este rompecabezas no tiene cuadrados, no hay fichas de dominó con una sola forma.
int blockNum = 10;
int needOverturn[] = { 0,0,1,1,1,1,0,1,0,1};
int needRotation[] = { 2,4,2,4,4,4,4,4,4,2 };
//翻转vector
template<typename T>
vector<T> frev(const vector<T>& v)
{
vector<T> ans;
ans.resize(v.size());
for (int i = 0; i < v.size(); i++)ans[i] = v[v.size() - 1 - i];
return ans;
}
//翻转二维vector的每一行
template<typename T>
vector<vector<T>> frev(const vector<vector<T>>& v)
{
vector<vector<T>>ans;
for (int i = 0; i < v.size(); i++)ans.push_back(frev(v[i]));
return ans;
}
//沿主对角线翻转二维vector
template<typename T>
vector<vector<T>> foverturn(const vector<vector<T>>& v)
{
vector<vector<T>> ans(v[0].size());
for (int i = 0; i < v[0].size(); i++) {
ans[i].resize(v.size());
for (int j = 0; j < v.size(); j++)ans[i][j] = v[j][i];
}
return ans;
}
//顺时针旋转二维vector
template<typename T>
vector<vector<T>> frotation(const vector<vector<T>>& v)
{
return frev(foverturn(v));
}
//得到骨牌的所有形态
vector<vector<vector<int>>> overturnOrRotation(int k)
{
vector<vector<vector<int>>> ans(0);
vector<vector<int>> vt = block[k];
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
vt = foverturn(vt);
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
return ans;
}3. Compresión de características
El problema de cobertura puede extraer características y convertirlo en un subproblema: el problema de cobertura de dominó cuadrado.
Usando el método de teñido por paridad, cualquier dominó se puede convertir en un tetradominó cuadrado, y cada una de las cuatro cuadrículas tiene un número natural.
P.ej:


Esto da:

La conversión según el método de numeración anterior es 2 1 0 2, y si se gira 90 grados, se convierte en 2 2 1 0
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[(i % 2 == 0) ? j % 2 : 3 - j % 2] += v[i][j];
}
}
return ans;
}Si se numera en el orden normal, sería
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[i % 2 * 2 + j % 2] += v[i][j];
}
}
return ans;
}4. Código completo
Genere todas las formas comprimidas primero, luego genere los identificadores de formas comprimidas correspondientes a todas las formas y combinaciones de fase (hasta 32)
De acuerdo con la solución de la forma comprimida, extienda la solución de bit de costo
//#include "t.h"
#include<iostream>
#include <vector>
using namespace std;
vector<vector<int>> block[] =
{
{
{1,1,1,1}
},
{
{1,0,1},
{1,1,1}
},
{
{1,1,0},
{0,1,0},
{0,1,1}
},
{
{1,1,0},
{1,1,1}
},
{
{1,0,0,0},
{1,1,1,1}
},
{
{1,0,0},
{1,1,1}
},
{
{0,1,0},
{0,1,0},
{1,1,1}
},
{
{1,1,0,0},
{0,1,1,1}
},
{
{1,0,0},
{1,0,0},
{1,1,1}
},
{
{1,1,0},
{0,1,1}
}
};
vector<vector<vector<int>>> shrinkBlocks;
vector<int> shrinkSum = { 14,12,11,10};
const int blockNum = 10;
int needOverturn[] = { 0,0,1,1,1,1,0,1,0,1 };
int needRotation[] = { 2,4,2,4,4,4,4,4,4,2 };
vector<int> shrink(const vector<vector<int>>& v)
{
vector<int> ans(4);
for (int i = 0; i < v.size(); i++) {
for (int j = 0; j < v[0].size(); j++) {
ans[i % 2 * 2 + j % 2] += v[i][j];
}
}
return ans;
}
//翻转vector
template<typename T>
vector<T> frev(const vector<T>& v)
{
vector<T> ans;
ans.resize(v.size());
for (int i = 0; i < v.size(); i++)ans[i] = v[v.size() - 1 - i];
return ans;
}
//翻转二维vector的每一行
template<typename T>
vector<vector<T>> frev(const vector<vector<T>>& v)
{
vector<vector<T>>ans;
for (int i = 0; i < v.size(); i++)ans.push_back(frev(v[i]));
return ans;
}
//沿主对角线翻转二维vector
template<typename T>
vector<vector<T>> foverturn(const vector<vector<T>>& v)
{
vector<vector<T>> ans(v[0].size());
for (int i = 0; i < v[0].size(); i++) {
ans[i].resize(v.size());
for (int j = 0; j < v.size(); j++)ans[i][j] = v[j][i];
}
return ans;
}
//顺时针旋转二维vector
template<typename T>
vector<vector<T>> frotation(const vector<vector<T>>& v)
{
return frev(foverturn(v));
}
//得到骨牌的所有形态
vector<vector<vector<int>>> overturnOrRotation(int k)
{
vector<vector<vector<int>>> ans(0);
vector<vector<int>> vt = block[k];
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
if (needOverturn[k] == 0)return ans;
vt = foverturn(vt);
for (int i = 0; i < needRotation[k]; i++) {
ans.push_back(vt);
vt = frotation(vt);
}
return ans;
}
// 生成枚举序号
template<typename T>
vector<vector<int>> foreach(const vector<vector<T>>&v)
{
int s = 1;
for (auto& vi : v)s *= vi.size();
vector<vector<int>> ans(s);
while (--s)
{
ans[s].resize(v.size());
int st = s;
for (int j = v.size() - 1; j >= 0; j--)
{
ans[s][j] = st % v[j].size();
st /= v[j].size();
}
}
return ans;
}
void jian(vector<int>&v, const vector<int> &v2)
{
for (int i = 0; i < v.size(); i++)v[i] -= v2[i];
}
bool allZero(const vector<int> &v)
{
for (auto &vi : v)if (vi)return false;
return true;
}
bool ok(const vector<int>& v)
{
vector<int> st = shrinkSum;
for (int i = 0; i < blockNum; i++)
{
jian(st, shrinkBlocks[i][v[i]]);
}
return allZero(st);
}
int main()
{
vector<vector<vector<vector<int>>>> blocks;
for (int i = 0; i < blockNum; i++)
blocks.push_back(overturnOrRotation(i));
shrinkBlocks.resize(blocks.size());
for (int i = 0; i < blocks.size(); i++)
{
for (auto &b : blocks[i])shrinkBlocks[i].push_back(shrink(b));
}
auto ids = foreach(blocks);
int s = 0;
for (auto &id : ids) {
if (!ok(id))continue;
s++;
cout << s << " ";
}
return 0;
}