Directorio de artículos
Matriz de Hesse y el valor extremo de la función multivariante
Una función univariante busca el valor extremo, como una función:
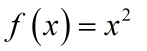
generalmente encuentra primero su primera derivada Según el teorema de Fermat, la primera derivada en el punto extremo debe ser igual a cero. Pero esta es solo una condición necesaria más que una condición suficiente. Para f (x) = x 2 , la función alcanza un valor extremo en el punto donde la primera derivada es 0, pero para f (x) = x 3 , es obvio que solo verificar la primera derivada no puede llegar a esta conclusión.
En este momento, es necesario encontrar otra derivada. Si la segunda derivada f '' (x) <0, entonces la función obtiene un máximo local en ese punto; si la segunda derivada f '' (x)> 0, entonces la función es Este punto obtiene un mínimo local; si f '' (x) = 0, el resultado aún es incierto y deben usarse otros métodos para determinar el valor extremo de la función.
Si desea encontrar puntos extremos en una función multivariante, el método es similar a este. Tome f = f (x, y, z) como ejemplo. Primero, para cada variable de la función, encuentra la derivada parcial por separado. En este momento, puedes saber dónde puede aparecer el punto extremo de la función. Es decir, a
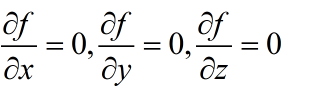
continuación, debes continuar encontrando la segunda derivada. En este momento, hay 9 derivadas parciales mixtas. , Si se expresa en forma de matriz,
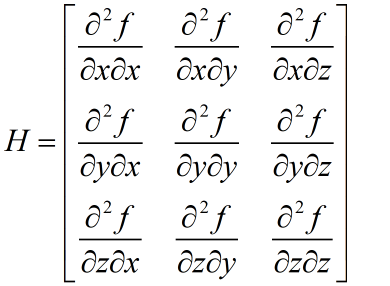
esta matriz se puede llamar hessiana. Por supuesto, lo que se da arriba es solo una matriz hessiana de tercer orden. Otras matrices de Hesse son similares.
Cuando la segunda derivada de la función unaria es igual a 0, no se puede determinar el valor extremo de la función en ese punto. De manera similar, frente a la matriz de Hesse, aún existe una situación donde no se puede determinar el valor extremo de una función multivariante, es decir, cuando el determinante de la matriz de Hesse es 0, es imposible determinar si la función puede obtener el valor extremo. Incluso es posible conseguir un punto silla, que es un punto que no es ni máximo ni mínimo.
Con base en la matriz de Hesse, se puede juzgar el valor extremo de la función multivariante y la conclusión es la siguiente:
(1) Si es una matriz definida positiva, el punto crítico es un mínimo local
(2) Si es una matriz definida negativa, el punto crítico es un máximo local
(3) Si es una matriz indefinida, el punto crítico no es extremos
cómo determinar si una matriz es definida positiva, definida negativa o indefinida. Uno de los métodos más utilizados es utilizar su principio secuencial. La condición necesaria y suficiente para que una matriz simétrica real sea una matriz definida positiva es que el principal y las subfórmulas de cada secuencia sean mayores que cero. Por supuesto, la cantidad de cálculo de este método de juicio es relativamente grande. Para las matrices cuadráticas reales, existe otro método de juicio: la condición necesaria y suficiente para que una matriz cuadrática real sea cuadrática definida positiva es que los valores propios de la matriz sean todos mayores que 0. La condición necesaria y suficiente para la forma cuadrática definida negativa es que los valores propios de la matriz sean todos menores que 0; de lo contrario, es indefinido.
Expansión de Taylor y matriz de Hesse
Realizando la expansión de Taylor de una función unaria f (x) en x 0 , podemos obtener: el
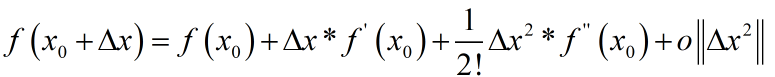
resto es el resto de Peano.
La parte derivada de segundo orden se asigna a un espacio bidimensional y multidimensional es la matriz de Hessain. En una imagen bidimensional, deje que f (x, y) represente el valor del píxel de la imagen en función de las coordenadas (x, y), luego expanda f (x + dx, y + dy) en f (x 0 , y) , Podemos obtener:

Exprese esta fórmula en una matriz y descarte el resto, entonces la fórmula será:

la segunda matriz en el tercer término en el lado derecho de la ecuación anterior es la matriz de Hesse en el espacio bidimensional, Se puede concluir que la matriz de Hesse es la segunda derivada en un punto del espacio.
El significado de la matriz de Hesse
La segunda derivada representa la ley de variación de la derivada. Si la función es una curva y la curva tiene una segunda derivada, entonces la segunda derivada representa la curvatura de la curva. Cuanto mayor sea la curvatura, más curva será la curva. Por analogía, la segunda derivada de un punto en el espacio multidimensional indica qué tan rápido cae el gradiente en ese punto. Tomando una imagen bidimensional como ejemplo, la derivada de primer orden es el cambio en el nivel de gris de la imagen, es decir, el gradiente de nivel de gris, y la derivada de segundo orden es el grado de cambio de gradiente de nivel de gris. Cuanto mayor es la derivada de segundo orden, menos lineal es el cambio de nivel de gris. (Es decir, cuanto mayor es el nivel de gris cambia, el gradiente lineal no lo es).
En una imagen bidimensional, la matriz de Hesse es una matriz definida positiva bidimensional con dos valores propios y dos vectores propios correspondientes. Los dos autovalores representan la anisotropía del cambio de imagen en las direcciones señaladas por los dos autovectores. Si el vector de característica y el valor de característica se utilizan para formar una elipse, la elipse marcará la anisotropía del cambio de imagen.
En una imagen bidimensional, qué tipo de estructura es la más isotrópica y qué tipo de estructura es más anisotrópica. Obviamente, el círculo tiene la isotropía más fuerte y cuanto más fuerte es la estructura lineal, más anisotrópica es la estructura.
Y cada valor característico debe tener las siguientes características:
| Valor propio 1 | Valor propio 2 | Característica de imagen |
|---|---|---|
| -Alto | -Alto | Estructura puntual (el primer plano es brillante) |
| + Alto | + Alto | Estructura puntual (el primer plano es oscuro) |
| Bajo | -Alto | Estructura lineal (el primer plano es brillante) |
| Bajo | + Alto | Estructura lineal (el primer plano es oscuro) |
Aplicación de la matriz de Hesse en el procesamiento de imágenes
La elipse formada por los autovalores y autovectores de la matriz mencionada anteriormente muestra la anisotropía de la imagen, y esta anisotropía se puede aplicar en el procesamiento de imágenes. En una imagen bidimensional, la estructura de puntos de la imagen es isotrópica, mientras que la estructura lineal tiene anisotropía. Por lo tanto, la matriz de Hesse se puede utilizar para mejorar la estructura lineal en la imagen y filtrar la estructura de puntos y los puntos de ruido. También se puede utilizar para encontrar la información del punto en la imagen y filtrar otra información.
Cuando se utiliza la matriz de Hesse, no es necesario realizar la expansión de Taylor de la imagen, simplemente busque los elementos en la matriz directamente. Generalmente, el método para obtener la derivación de segundo orden para una imagen bidimensional es el siguiente:

Sin embargo, este método es muy robusto y susceptible a la interferencia de señales locales en la imagen. Incluso se puede decir que este método de derivación es controvertido. Debido a este punto, la segunda derivada también se puede expresar de las siguientes maneras:

Además de los dos métodos de representación anteriores, la segunda derivada también se puede expresar de otras maneras y, a menudo, métodos diferentes obtienen valores diferentes, porque este método solo incluye Se incluye la información de los tres puntos incluido el mismo, y la cantidad de información es insuficiente. Por lo tanto, de acuerdo con la teoría del espacio de escala lineal (LOG), la derivada de una función es igual a la convolución de la función y la derivada de la función gaussiana. Como se muestra a continuación:

Dado que la plantilla gaussiana puede incluir la información de todos los puntos en el rango circundante, no habrá errores. Entonces, cuando use la imagen para encontrar los elementos en la matriz de Hesse, simplemente convierta la imagen con la segunda derivada de la función gaussiana. Es decir:
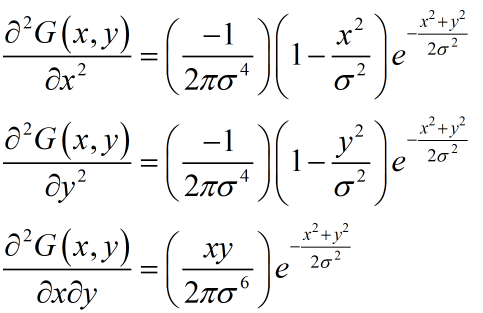
al escribir un programa, solo necesita convolucionar la imagen con tres plantillas de antemano para generar un mapa de tres derivadas parciales, y luego indexar las derivadas parciales de las posiciones correspondientes según sea necesario.
Después de procesar la imagen, la mayoría de las estructuras lineales de la imagen se mejorarán, pero algunas estructuras finas no se mejoraron demasiado y también hay agujeros en algunas estructuras gruesas, lo que está relacionado con el tamaño de la ventana de derivación. Si la ventana es demasiado pequeña, habrá huecos en muchas estructuras gruesas, porque el área central se considera una estructura de puntos. Si la ventana derivada es demasiado grande, es fácil perder la estructura fina. Además, la selección de la varianza de la plantilla gaussiana también afecta el tamaño de la derivada parcial. De hecho, este método usa la segunda derivada de un kernel gaussiano con una varianza de s para generar un kernel de detección, que se usa para medir el contraste entre las regiones interna y externa dentro del rango de la dirección derivada (-s, s).

Sin embargo, en la misma imagen, el grosor de la estructura lineal es definitivamente diferente y el mismo tamaño de ventana no es aplicable a todos. Para resolver este problema, puede utilizar el método de múltiples plantillas. Es decir, usar plantillas gaussianas de escala múltiple y convolución retrógrada para un punto, y luego seleccionar el resultado más anisotrópico como la salida del punto.
Según la matriz de Hesse, también se pueden determinar los puntos de las esquinas en una imagen, es decir, los dos valores propios mencionados en la tabla anterior tienen valores absolutos grandes. Esta es la idea de la detección de esquinas de Harris.
Algoritmo de simplificación hessiano basado en el espacio de escala
Para una imagen bidimensional I, la matriz de Hesse describe la derivada bidimensional de cada píxel en la dirección principal:
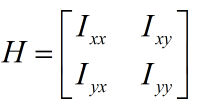
según la teoría del espacio de escala, la segunda derivada se puede obtener mediante la convolución de la imagen y la función gaussiana, por ejemplo en el punto (x, y) Existen:
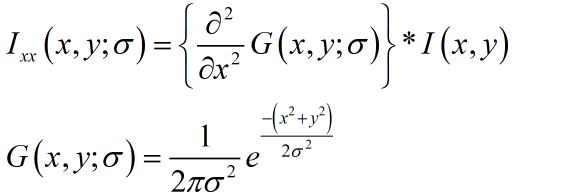
según la definición para encontrar los autovalores de la matriz de segundo orden, la solución de los autovalores de la matriz de Hesse,
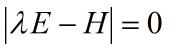
y según las características de la imagen, podemos obtener:

Sustituya la ecuación anterior para obtener la solución de valores propios de hessiano: