Impulso de respuesta y convolución

Esta serie es una serie de notas en video de la serie básica de matemáticas de ingeniería DR_CAN. Para obtener más detalles, consulte https://space.bilibili.com/230105574.
Debido al nivel limitado del autor, inevitablemente hay algunas deficiencias y errores en el texto. Sinceramente, le invito a que me critique y corrija.

1 Definición de convolución

Función \ (f, g \) se define en la (R ^ {n} \) \ en función medible (función medible), \ (f, g \) convolución hace referencia como \ (F * G \) , Es la integral del producto de otra función después de que se voltea y se traduce , y es una función de la cantidad de traducción, es decir:

\ [(f * g) (t) \ stackrel {\ text {def}} {=} \ int _ {\ mathbb {R} ^ {n}} f (\ tau) g (t- \ tau) d \ tau \]

Si la función no está definida en \ (R ^ {n} \) , puede especificar todos los valores fuera del dominio de la función como cero, de modo que se convierta en una función definida en \ (R ^ {n} \) .

2 Definición de respuesta al impulso

En el procesamiento de señales , la respuesta de impulso (inglés: respuesta de impulso) generalmente se refiere a la salida (respuesta) del sistema cuando la entrada es una función de pulso unitario , que es una de las respuestas transitorias . Para sistemas de tiempo continuo , la respuesta al impulso generalmente está representada por la función \ (h (t, \ tau) \) , y la señal de entrada correspondiente, es decir, la función de impulso de la unidad satisface la forma de la función delta de Dirac , se define de la siguiente manera:

\ [\ delta (t) = 0, t \ neq 0 \\\ int _ {- \ infty} ^ {\ infty} \ delta (t) dt = 1 \]

Cuando la entrada es una función delta de Dirac , la respuesta de impulso del sistema \ (h (t) \) contiene toda la información del sistema. Entonces, para cualquier señal de entrada \ (x (t) \) , puede usar el método de convolución de dominio continuo para obtener la salida correspondiente \ (y (t) \) . Eso es:

\ [y (t) = \ int _ {- \ infty} ^ {\ infty} x (\ tau) h (t- \ tau) d \ tau = x (t) * h (t) \]

Para sistemas de tiempo discreto, la respuesta al impulso generalmente está representada por la secuencia \ (h [n] \) . La señal de entrada discreta correspondiente, es decir, la función de pulso unitario satisface la forma del delta de Kronecker , en la ciencia de señales y sistemas. Las funciones se pueden definir de la siguiente manera:

\ [\ delta [n] = \ left \ {\ begin {array} {ll} 1, & n = 0 \\ 0, & n \ neq 0 \ end {array} \ right. \]

Del mismo modo, cuando la entrada es \ (\ delta [n] \) , la respuesta al impulso del sistema discreto \ (h [n] \) contiene toda la información del sistema. Entonces, para cualquier señal de entrada \ (x [n] \) , la señal de salida correspondiente \ (y [n] \) puede obtenerse mediante el método de convolución (suma) de dominio discreto . Eso es:

\[y[n]=\sum_{k=0}^{\infty} x[k] h[n-k] \]

3 sistema lineal invariante en el tiempo

4 ejemplos de sistemas de amortiguación de muelles

Para un sistema lineal, su salida correspondiente \ (x (t) \) es igual a la entrada \ (f (t) \) y su función de transferencia \ (H (s) \) después de la transformación inversa de Laplace Convolución de la respuesta al impulso \ (h (t) \) :

Dividimos la parte discreta de la señal de entrada en tres \ (\ Delta T \) , estas tres partes tendrán un efecto en el sistema, y ​​los efectos son independientes entre sí, es decir, la respuesta de entrada independiente correspondiente, es decir, la salida. La salida del sistema \ (t \) en un momento determinado es la suma de las respuestas de entrada antes del tiempo de \ (t \) . Cuando \ (\ Delta T \ rightarrow 0 \) , esta suma se convierte en una integral :

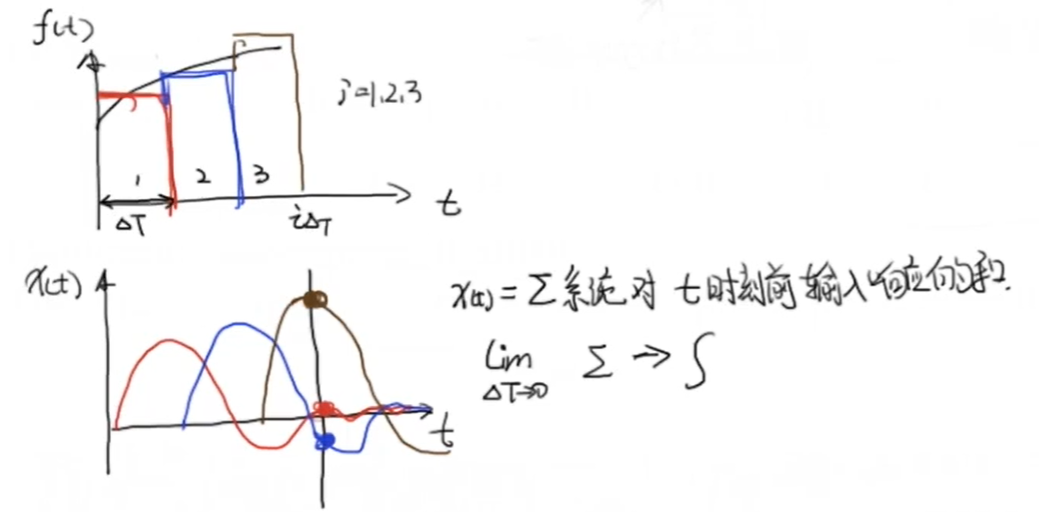
De manera similar, cuando \ (\ Delta T \ rightarrow 0 \) , esta pequeña entrada en el tiempo \ (t \) se puede aproximar como \ (f (t) \) veces de la función de impulso . De acuerdo con la naturaleza del sistema lineal invariante en el tiempo, podemos obtener esta tabla de entrada y salida:

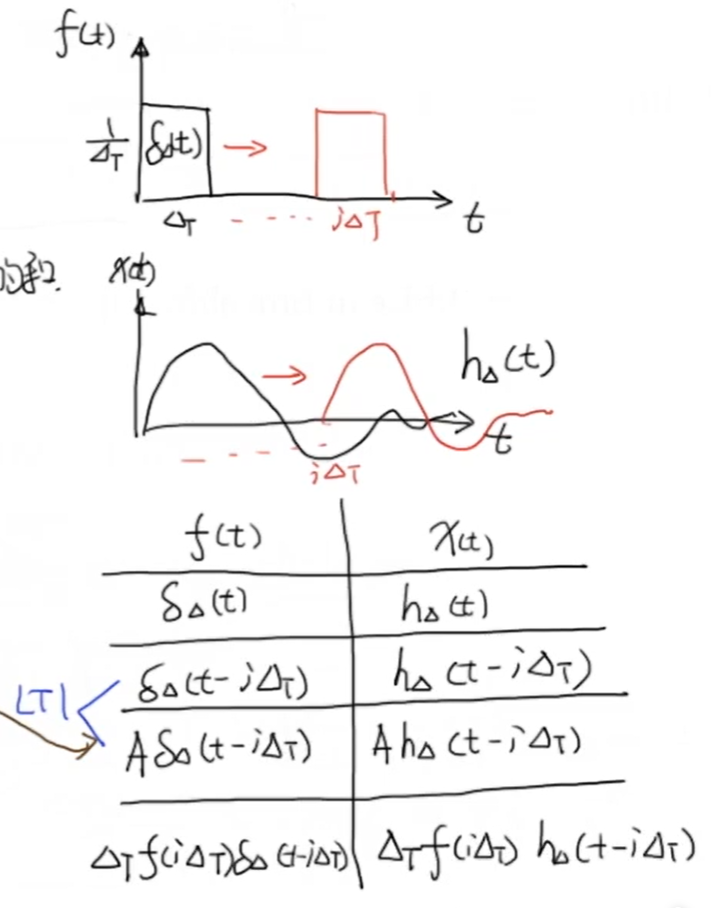
La primera línea es el impacto de un impacto, que puede entenderse como una forma básica.

La segunda línea indica que después de que esta descarga se retrase en \ (i \ Delta T \) , la respuesta de entrada también se retrasará \ (i \ Delta T \)

La tercera línea significa que cuando la intensidad de impulso (área de imagen) es \ (A \) , y después de \ (i \ Delta T \) se retrasa, la respuesta de entrada del sistema se retrasará en la forma básica \ (i \ Delta T \) un \ (a \) veces

La cuarta línea es la promoción de la tercera línea. Al reemplazar \ (A \) con la función de entrada en el momento de \ (i \ Delta T \) , el área del segmento \ (\ Delta T \) . Se indica que el área de un sistema de \ (\ Delta T f (i \ Delta T) \) que incide sobre un retardo de entrada \ (i \ Delta T \) de respuesta de entrada después de

De acuerdo con el principio de superposición, podemos agregar todas las entradas antes de este momento, para que podamos obtener la respuesta del sistema en este momento. Se puede escribir como:

\ [x (t) = \ sum_ {i = 0} ^ {j} \ Delta T f \ left (i \ Delta T \ right) h_ {0} (ti \ Delta T) \ quad t = j \ Delta T \]

Cuando \ (\ Delta T \ rightarrow 0 \) , \ (i \ Delta T = \ tau \) , la fórmula anterior se puede escribir en forma de convolución :

\ [x (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) h (t- \ tau) d \ tau = f (t) * h (t) \]

5 inspiración

A través del análisis anterior, podemos encontrar que para un sistema lineal invariante en el tiempo, la respuesta al impulso \ (h (t) \) puede definir completamente el sistema. Es por eso que expresamos la función de transferencia como \ (H (s) \) , es decir, la respuesta al impulso \ (h (t) \) obtiene la función de transferencia después de la transformación de Laplace \ (H (s) \) .