\ (T1 \) line up
Description
Grab dinner is a part of high school life, and now has a team of length \ (the n-\) , ( Note: Due to keep the distance between people and different situations keeping a distance of different sizes, so the length of the queue does not directly reflect the number of people) . The distance between men and men are known as \ (A \) , the distance between men and women is a b b, the distance between the female is \ (c \) . A male Dafan time \ (D \) , a girl Dafan time \ (E \) , the sum of the queue time required in all cases (ignoring the contribution ranks of the body size of the length), the answer to $ 10 ^ {9} $ modulo +7.
Input Format
Line six integer \ (n-\) , \ (A \) , \ (B \) , \ (C \) , \ (D \) , \ (E \) .
Output
An integer line, that is the answer.
Solution
First, it is easy to think of a DP practice, where we construct \ (f \) \ ([i] [0/1] \) array, represents the last person in the case of 0/1, the last person to hit rice of the time and, 0 represents the last one is male, one is female.
Definition of G \ ([I] [0/1] \) Total number represents the last program in the case where a person is in. Hand push the state transition equation:
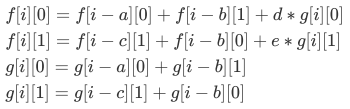
But we will find that \ (n \) is very large, but \ (A \) , \ (b \) , \ (c \) , is very small, so each time you transfer the required \ (ia \) , \ (ib \) , \ (ic \) it is very close, so you can consider using the scroll array transfer.
But did not make the scroll array optimized for time.
Here we use the transfer matrix multiplication instead, only a configuration \ (4 * max (a, b, c) \) transfer matrix to order.
Let's talk about the detailed structure of the matrix! !
First seen \ (g \) array of (f \) \ transfer array had an impact, so we not just transfer matrix \ (f \) , must also join \ (g \) transfer.
Normally, the initial matrix construct a long way:

However, considering the \ (F \) \ ([I] [0/1] \) and G \ ([I] [0/1] \) of the four to be transferred with the stuff, so each \ (I \) to maintain the value of four, so maintaining four values in each block, it becomes:

Okay, so that you can explain why \ (4 * max (a, b, c) \) order, the order is the length and width of the matrix meaning friends
Then the matrix structure on one goal:
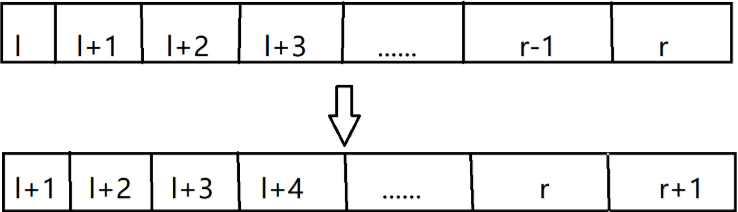
This means that the \ (R & lt \) Release \ (R & lt. 1 + \) , and then against the transfer equation dp configured above a transfer matrix alone.
Shaped like:

After completion of the transfer matrix configuration fast power, quickly get the final answer \ (F [n-] [0] \) + \ (F [n-] [. 1] \)
Details : When the code is implemented because as every one four, so we use \ (<< 2 \) (equivalent to x 4) positions may be quickly i corresponds to each matrix, each block is selected by | (= add operation or operation) to process the code simple.
#include<bits/stdc++.h>
#define ll long long
#define N 150
using namespace std;
const int mod=1e9+7;
ll n;
int a,b,c,d,e,O;
int g[N][2],f[N][2];// f[i][0/1]表示长度为i的队伍最后为男生(0)或女生(1)的答案 g[i][1/0]与f一样,不过是记录到达这个状态的方案数
struct Matrix{
int a[N][N];
Matrix(){memset(a,0,sizeof(a));}
}T,qs,asd;//T为转移矩阵 qs为初始矩阵
void mul(Matrix &CC,Matrix A,Matrix B)
{
Matrix C;
int i,j;
for(i=0;i<O;i++)
for(j=0;j<O;j++)
C.a[i][j]=0;
for(i=0;i<O;i++) //两个矩阵的相乘
for(j=0;j<O;j++)
if(A.a[i][j])
{
for(int k=0;k<O;k++)
if(B.a[j][k])
C.a[i][k]=(1ll*A.a[i][j]*B.a[j][k]+C.a[i][k])%mod;
}
CC=C;
}
void Ksm(Matrix &CC,Matrix AA,ll t) //标准快速幂
{
Matrix A,C;
t--;
A=C=AA;
while(t)
{
if(t&1)
{
mul(C,C,A);
}
mul(A,A,A);
t>>=1;
}
CC=C;
}
int main()
{
int i,j;
scanf("%lld",&n);
scanf("%d%d%d%d%d",&a,&b,&c,&d,&e);
g[0][0]=g[0][1]=1; //初始化
f[0][0]=d,f[0][1]=e; //初始化
int o=max(a,max(b,c)); //转移所需的最小的矩阵
O=o<<2;//矩阵长宽
for(i=1;i<o;i++)// 初始化第一个矩阵
{
if(i>=a) (f[i][0]+=f[i-a][0])%mod,(g[i][0]+=g[i-a][0])%mod;
if(i>=b) (f[i][0]+=f[i-b][1])%mod,(g[i][0]+=g[i-b][1])%mod,(f[i][1]+=f[i-b][0])%mod,(g[i][1]+=g[i-b][0])%mod;
if(i>=c) (f[i][1]+=f[i-c][1])%mod,(g[i][1]+=g[i-c][1])%mod;
f[i][0]=(1ll*g[i][0]*d+f[i][0])%mod;
f[i][1]=(1ll*g[i][1]*e+f[i][1])%mod;
}
//下面开始把我们构造的转移矩阵完善一下
for(i=1;i<o;i++)
{
for(j=0;j<4;j++)
T.a[i<<2|j][(i-1)<<2|j]=1; //把矩阵中的1全填了再说
}
T.a[(o-b)<<2][(o-1)<<2|1] = T.a[(o-b)<<2|2][(o-1)<<2|3] = T.a[(o-b)<<2|1][(o-1)<<2] = T.a[(o-b)<<2|3][(o-1)<<2|2] = 1; //把公式中的全部i-b的影响填上1
T.a[(o-b)<<2|2][(o-1)<<2|1] = e; T.a[(o-b)<<2|3][(o-1)<<2] = d; //把e和d填上
//后面也在一个一个填数
++T.a[(o-a)<<2][(o-1)<<2]; ++T.a[(o-a)<<2|2][(o-1)<<2|2];
(T.a[(o-a)<<2|2][(o-1)<<2]+=d)%mod;
++T.a[(o-c)<<2|1][(o-1)<<2|1]; ++T.a[(o-c)<<2|3][(o-1)<<2|3];
(T.a[(o-c)<<2|3][(o-1)<<2|1]+=e)%mod;
for(i=0;i<o;i++) //把之前求出的初始f付给这个初始矩阵
{
qs.a[0][i<<2] = f[i][0];
qs.a[0][i<<2|1] = f[i][1];
qs.a[0][i<<2|2] = g[i][0];
qs.a[0][i<<2|3] = g[i][1];
}
Ksm(T,T,n-o+1); mul(qs,qs,T); //快速转移
printf("%d\n",(qs.a[0][(o-1)<<2]+qs.a[0][(o-1)<<2|1])%mod); //取最后的答案
return 0;
}