#NOIP former mathematics knowledge summary

I'm good food ah ......

Euler function

Euler function φ (n), is the number of positive integer less than n and relatively prime and n (including 1).

nature:

1. For the prime number n:

$ F (n) = n-1 $

 

2 .. For P = n- ^K

$φ(n)=(p-1)*p^{k-1}$

3. The function of the properties of the product:

For prime m, n, are:

$ F (n * m) = z (n) * z (m) $

4. Calculate the Euler function:

$φ(n)=n*\Pi (1-\frac{1}{p_i})$

The demand is less than n and prime with n number and:

$ S = n * f (n) / 2 $

Euler's theorem

For prime a, m, are:

$a^{\varphi (m)}\equiv 1(mod\  m)$

Euclid's theorem

$gcd(a,b)=gcd(b,a\ mod\ b)$

Extended Euclid

Known that a, b, solving a set of x, y, so that they meet ax + by = gcd (a, b)

prove:

ax+by=gcd(a,b);

1. (1) a = 0，ax+by = gcd(a,b) = gcd(0,b) = b,

At this time, x = 0 (at this time is arbitrary value of x), y = 1;

    (2)b = 0, ax + by = gcd(a,b) = gcd(a,0) = a,

At this time, x = 1, y = 0 (at this time the value of y is optional);

2.a and b is not 0

ax1 + by1 = gcd(a, b)

A Euclid Theorem: gcd (a, b) = gcd (b, a% b) to give

ax1 + by1 = gcd (a, b) = gcd (b, a% b) that is:

bx2 + a%by2 = gcd(b, a%b) = ax1 + by1

a % b = a - a/b*b;

ax1 + by1 = bx2 + (a - a/b*b)y2;

                =bx2 + ay2 - a/b*b*y2;

                =ay2 + b(x2-a/b*y2);

Therefore: x1 = y2, y1 = x2 - a / b * y2

 

int exgcd(int a,int b,int &x,int &y,int c)
{
    if(!b)
    {
        x=c/a;
        y=0;
        return a;
    }
    int g=exgcd(b,a%b,y,x,c);
    y-=a/b*x;
    return g;
}

View Code

 

 

 

Fermat's Little Theorem

For the prime number p, arbitrary integer a, and a, p prime, are:

$a^p\equiv a(mod\  p)$,即$a^{p-1}\equiv 1(mod\  p)$

Multiplicative inverse

And then divided by a number equivalent to the modulo this number multiplied by the inverse element and then modulo

which is

$(a/b)\ mod\ p=(a*inv[b])\ mod\ p$

A number x modulo p at not necessarily inverse element, x is present in inverse element for p if and only if x and p coprime

 The method of seeking inverse:

1. Fermat's little theorem fast power +

Fermat's little theorem from the readily available $ a * a ^ {p-2} \ equiv 1 (mod \ p) $

Therefore $ a ^ {p-2} $ is also desired (required a, p prime!)

2. Push inverse linear

!! 1 ~ n to find the inverse element:

$inv[i] =inv[i+1]*(i+1) (mod\ p)$

inline void get_finv()
{
    fac[1]=finv[0]=1;
    for(int i=2;i<=n;++i;++i)
        fac[i]=fac[i-1]*i%mod;
    finv[n]=quick_pow(fac[n],mod-2);
    for(int i=n-1;i;--i)
        finv[i]=finv[i+1]*(i+1)%mod;
}

View Code

 

prove:

 fac[i] * inv[i] ≡1 (mod p) fac[i+1] * inv[i+1] ≡1 (mod p) => fac[i]* (i+1) * inv[i+1] ≡1(mod p) 由 同余的除法原理可得 : inv[i] ≡inv[i+1] * (i+1) 推导完毕

 

 

Seeking the inverse element 1 ~ n:

$inv[i]=inv[p\ mod\ i] * (- p/i) (mod\ p)$

inline void get_inv()
{
    inv[0]=inv[1]=1;
    for(int i=2;i<=n;++i)
        inv[i]=inv[mod%i]*(mod-mod/i)%mod;
}

View Code

prove:

  令 s = p/i , t = p%i , 则有： s*i + t = p (显然) 然后 s*i + t ≡ 0 (mod p) 移项得 t ≡ -s*i (mod p) 同除以 t * i 得 t / (t*i) ≡ -s*i / (t*i) (mod p) 将除法转化为乘法 => inv[i] ≡ -s * inv[t] (mod p) 于是将 s=p/i , t=p%i带入就可以得到: inv[i] ≡ inv[p%i] * (-p/i) (mod p) 推导完毕

 

 

3. Extended Euclid

$ AxΞ1 (v \ b) $

-->$ax+by=1$

Using a spread-solving Europe

//转载 from Judge
#define ll long long
const int mod=; //同上
 void ex_gcd(ll a,ll b,ll &x,ll &y){
    if(!b){ x=1,y=0; return ; }
    ex_gcd(b,a%b,x,y);
    ll t=x; x=y,y=t-(a/b)*y;
 }
 //当然你也可以这么写,更能体现公式: 
 //  ll X=x,Y=y;
 //  x=Y,y=X-(a/b)*Y;
 inline ll inv(ll a){
    ll inv_a,y;
    ex_gcd(a,mod,inv_a,y);
    return inv_a;
 }

View Code

 

Chinese remainder theorem

Solving congruence equation

xΞa₁(mod m₁)

xΞa₂(mod m₂)

XΞa ₃ (m No by mod ₃ )

......

xΞa_k(mod m_k)

Wherein A _{. 1} A ₂ A _{. 3} ... A _K pairwise mass

X seeking the smallest non-negative integer solution

Theorem content

Make LCM = M (m _{. 1 ~ K} ), i.e., $ M = m_1 * m_2 * m_3 * ... * m_k $

T _I is

 

Solution of the smallest non-negative integer

We certainly have a solution for the

 

The general solution $ x + i × M $

Is the smallest non-negative integer solution $ (M + x \ mod \ M) \ mod \ M $

 

// Ti Congruence can be extended Euclidean solving 

void exgcd ( int A, int B, int & X, int & Y) 
{ 
    IF (B == 0 ) {= X . 1 ; Y = 0 ; return ;} 
    exgcd (B, A % B, X, Y);
     int TP = X; 
    X = Y; Y = TP-A / B * Y; 
} 

int China () 
{ 
    int ANS = 0 , LCM = . 1 , X , Y;
     for ( int I = . 1 ; I <= K; I ++) = LCM *B [I];
     for ( int I = . 1 ; I <= K; ++ I) 
    { 
        int TP = LCM / B [I]; 
        exgcd (TP, B [I], X, Y); 
        X = (X B% [I] + B [I])% B [I]; // X to a minimum non-negative integer solution 
        ANS = (TP + ANS * X * A [I])% LCM; 
    } 
    return (ANS + LCM )% LCM; 
}

View Code

 

Extended Chinese remainder theorem

Solution m _{. 1} , m ₂ , m _{. 3} ... m _n- without prime.

Considering only m _{. 1} , m ₂ situation:

Based solution is x

Available

$x=a_1+k_1*m_1 ; x=a_2+k_2*m_2$

$a_1+k_1*m_1 = a_2+k_2*m_2$

$k_2*m_2-k_1*m_1=a_1-a_2$

Very similar form and congruence equation expanding Europe solvable

= GCD set G (m _{. 1} , m ₂ )

If the $ a_1-a_2 $ g is not a multiple of no solution Liao (see conditions exgcd Solution of a congruence equation solvability)

Otherwise Solving this congruence equation

The final solution $ \ times \ frac {c} {g} $ available k_1 $ $

A $ x = -k_1 \ times m_1 + a_1 $ solve for x

The general solution $ X = x + k \ times lcm (m_1, m_2) $

Finally obtained $ x = x_0 (mod lcm (m_1, m_2)) $

So, de-n times spread to Europe to get the final solution.

 

#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
const int N=100005;
int n;
ll m[N],a[N];
ll exgcd(ll a,ll b,ll &x,ll &y)
{
    if(!b)
    {
        x=1;y=0;
        return a;
    }


    ll gcd=exgcd(b,a%b,y,x);
    y-=(a/b)*x;
    return gcd;
}

ll excrt()
{
    ll x,y,lcm=m[1],ans=a[1],gcd;
    for(int i=2;i<=n;i++)
    {
        gcd=exgcd(lcm,m[i],x,y);
        if((ans-a[i])%gcd)return -1;
        x=(ans-a[i])/gcd*x%m[i];
        ans-=lcm*x;
        lcm=lcm/gcd*m[i];
        ans%=lcm;
    }
    return (ans%lcm+lcm)%lcm;
}
void work()
{
    for(int i=1;i<=n;i++)
        scanf("%lld%lld",&m[i],&a[i]);
    cout<<excrt()<<endl;
}
int main()
{
    while(scanf("%d",&n)==1)work();
    return 0;
}

View Code

Permutations

Number of permutations

The number of different permutations of all elements taken m (m <= n) from n different elements.

$A_n^m=n(n-1)(n-2)\cdots(n-m+1)=\frac{n!}{(n-m)!},\quad n,m\in \mathbb{N}^* ,\text{并且}m\leq n$

In particular, a predetermined 0! = 1.

The number of combinations

Remove the m elements (m <= n) of the number of all the different combinations from the n different elements.

$C_n^m=\frac{A_n^m}{A_m^m}=\frac{n(n-1)(n-2)\cdots (n-m+1)}{m!}=\frac{n!}{m!(n-m)!},\quad n,m\in \mathbb{N}^* ,\text{并且}m\leq n$

Predetermined $ C_n ^ 0 = C_n ^ n = 1 $

Binomial theorem

Common forms

$(x+1)^n=\sum_{i=0}^{n} C(n,i) ~ x^i$

prove:

(x+1)ⁿ=(x+1)*(x+1)*...*(x+1)

From the n (x + 1) in the selected n times x or may select only one.

So the answer is each selected result is multiplied by n elements will accumulate

And a case where i is selected from the n x (x + 1) is the number of

^{$C_n^i$}

QED.

 

Lucas Theorem

Theorem content

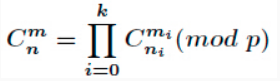
prove

(Gugu Gu)

Code 

ll C(ll x,ll y,ll mod)
{
    if(x<y)return 0;
    return fac[x]*qpow(fac[y],p-2,p)%p*qpow(fac[x-y],p-2,p)%p;
}
ll lucas(ll x,ll y,ll p)
{
    if(!y)return 1;
    return C(x%p,y%p,p)*lucas(x/p,y/p,p)%p;
}

View Code

 

 

 

φ(n)=n−1