Have you ever noticed that when you take an image of a flat rectangular object, the corners are rarely at 90°?
Perspective projection distorted rectangle
This phenomenon is characteristic of perspective projection, in which points in a three-dimensional scene (for example, the corners of a rectangle) are projected through a pinhole¹ onto a flat surface (a camera image sensor). Line segments closer to the camera are longer than segments of the same length farther from the camera. Right angles may become acute or obtuse angles, and parallel lines may converge toward a vanishing point.
Perspective distortion can be a problem in automatic inspection of planar objects. Since we want to check that the object's features have the correct shape and size, we want to "reverse" the perspective distortion. If we can do this, we can obtain an image that makes the object appear as if the camera axis is perpendicular to the object's surface.
Demonstrates the effect of reversing perspective distortion. In this case, the book corner is mapped to an arbitrary point in the shape of a square with a red circle. The image on the right is better suited for automated inspection as it can be easily positioned and compared to the template.
We want to warp an image affected by perspective distortion into an image that is restored on the plane of interest: angular distortion is minimal and three-dimensional parallel lines appear parallel.
OpenCV provides two functions that can do this: warpAffine() and warpPerspective(). They have the same signature, but warpAffine() requires a 2x3 transformation matrix, while warpPerspective() requires a 3x3 transformation matrix. These matrices are calculated by the functions getAffineTransform() and getPerspectiveTransform() respectively. The former expects three matching pairs of coordinates, while the latter expects four matching pairs of coordinates. Intuitively, it is easier to get three contrasts than four pairs, so the question is: under what circumstances can we get away from using a perspective transformation and use an affine transformation with three pairs of coordinates?
To answer this question, let us consider the two images in Figure 3.
Left: chessboard image, camera distance is about 1 meter Right: chessboard image, camera distance is about 7 meters
Even though the board didn't move between the two shots, the pattern looks different. In the image on the right, the camera is about 7 meters away from the object, and the parallelism of the lines is maintained better than in the image on the left. If we calculate the affine and perspective transformations and then distort these images accordingly, we get the images shown in Figures 4 and 5.
Affine transformation of the image in Figure 3. Points A, B and C on the chessboard are mapped to the corresponding arbitrary points marked with red circles
Perspective transformation of the image in Figure 3. Points A, B, C and D on the chessboard are mapped to the corresponding arbitrary points marked with red circles
Figure 4 shows the effect of the affine transformation, using points A, B and C. The image on the right, taken at about 7 meters, is reasonably compensated, although not perfect (see Figure 6). The image on the left is still heavily distorted because point D (which is not even visible in the image) is not projected anywhere near its corresponding red circle.
Details of Figure 4. Point D (blue disk) is projected near the center of the red circle, but not exactly on the center
Figure 5 shows the effect of perspective transformation. Due to the four coplanar points A, B, C and D used to calculate the transformation matrix, the perspective distortion is well compensated in both cases and the images look the same. The criterion we should use is to maintain parallelism of lines. Affine transformations preserve the parallelism of lines. If the object to be detected has parallel lines in the three-dimensional world, and the corresponding lines in the image are parallel (such as the right case of Figure 3), then an affine transformation is sufficient. On the contrary, if the parallel lines in the three-dimensional world diverge in the image (such as the left case of Figure 3), then the affine transformation is not enough: we need a perspective transformation.
Derivation of perspective transformation
The perspective transformation that relates a planar scene to pixel coordinates comes from the general case of 3D to 2D projection through a pinhole:
where f is the focal length, (lx, ly) are the physical dimensions of the pixel, and (cx, cy) is the optical center of the camera in pixels. Equation (1) explicitly shows how the pinhole camera model projects a three-dimensional point (X, Y, Z) to image coordinates (u, v), ultimately scaling by a factor λ. Read from right to left, it states:
Convert points in world coordinates to coordinates in camera coordinates, by rotation and translation, and then project these coordinates onto the sensor plane.
The shape of the projection matrix P is 3x4. The connection to perspective transformation comes from the assumption that the scene (where point (X, Y, Z) is) is a plane. Therefore, Z = αX + βY + γ:
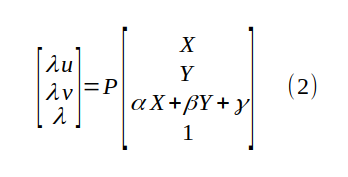
Mixing the entries of P in equation (2) with α, β and γ in equation (2), we get a new 3x3 unknown matrix M, the perspective transformation matrix:
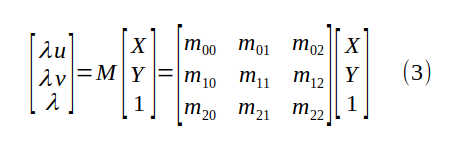
To solve for the terms of M, we first have to substitute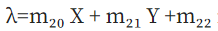 
in equation (3), which gives us two homogeneous linear equations in nine unknowns: a>
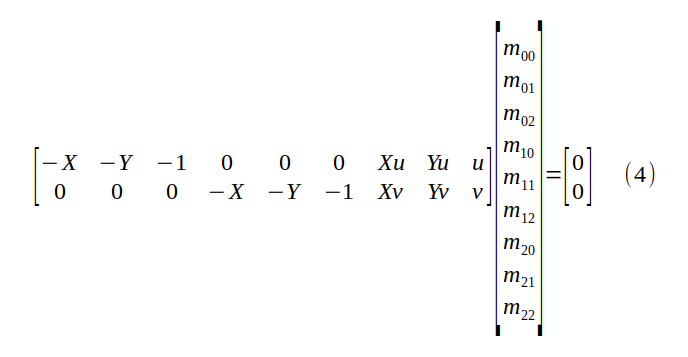
We can solve for the nine entries (scaling factors) of the perspective transformation matrix M by the correspondence between the four object plane coordinates (X, Y) and their pixel values (u, v), four of which correspond (thus eight linear equations) are sufficient.
We have nine unknowns. Since each correspondence gives us two linear equations in nine unknowns, why would four correspondences (and therefore eight linear equations) be enough?
Because we are dealing with a homogeneous linear equation, that is, the right-hand side of equation (4) is the zero vector. If we add a 9th independent linear equation we will be stuck with the trivial solution
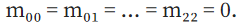
middle. By solving four pairs of linear equations in equation (4), we obtain solutions that can be scaled by multiplying by any non-zero factor. We usually use this degree of freedom setting as:
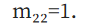
Affine transformation
As we stated earlier, affine transformations preserve the parallelism of lines. This means that a parallelogram will always map to another parallelogram. When we calculate the perspective transformation matrix using four correspondences of two parallelograms (such as the right case of Figure 5), we observe that the entries m_20 and m_21 are very close to zero. You can check this observation empirically by comparing the perspective transformation matrix between a general quadrilateral and a parallelogram with this script.
The third row of the perspective transformation matrix mapping two parallelograms is approximately [0 0 1]
If you're not satisfied with empirical observations, here's a more convincing argument:
Mapping a parallelogram to another parallelogram can be broken down into translation, rotation, shear, axis scaling, shear, rotation and translation (plus optional reflection). Each of these transformations can be represented by a matrix whose third row is [0 0 1], so their multiplication
Equation (3) for the special case of affine transformation can then be written as:
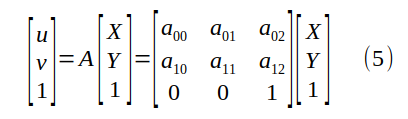
Here we use the degrees of freedom of the perspective transformation matrix, arbitrarily setting a_{22}=1, and by doing this, we get rid of the (annoying) lambda multiplier. We can rearrange the terms to tile the entries of the affine transformation in an unknown vector:
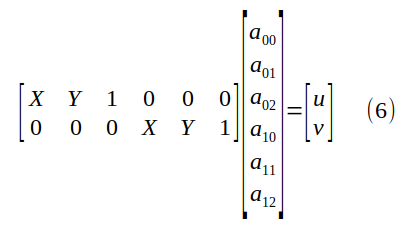
By (6), each correspondence gives us two linear equations in 6 unknowns. This is why three correspondences are sufficient to define an affine transformation matrix.
in conclusion
We solve the problem of mapping coordinates of a planar scene to pixel coordinates from a set of correspondences. The central question of this article is which type of transformation to choose, perspective or affine. The transformation does not map object features to their theoretical positions, except for three corresponding points. After digging deeper into the origins of the perspective transformation matrix, the special case of the affine transformation matrix must take care to maintain parallelism in order to decide on the type of transformation.
· END ·
HAPPY LIFE
This article is for learning and communication only. If there is any infringement, please contact the author to delete it.