Secure multi-party convex hull protocol based on quantum homomorphic encryption

Summary

Secure Multiparty Computational Geometry (SMCG) is a branch of secure multiparty computation. This protocol is designed for safe multi-square convex hull computation in SMCG. First, a secure two-party value comparison protocol based on quantum homomorphic encryption is proposed. Due to the nature of quantum homomorphic encryption, this protocol can well protect the security of data and the interaction between parties during the execution of quantum circuits. The results are announced by a semi-trusted third party. Using the value comparison protocol designed above, a secure multi-party convex hull protocol is proposed, which can safely solve the common convex hull problem of multiple user point sets. Then the correctness and security analysis is carried out, which proves that the protocol is safe and reliable.

background

With the development of information technology, security issues have always been a hot issue in the academic community. Secure Multiparty Computation (SMC) aims to solve the problem of multiple mutually distrustful participants jointly computing a certain type of task while protecting their information from being leaked. SMC originated from the millionaire problem proposed by Yao in 1982, where two millionaires compare their wealth without knowing each other's wealth. It involves various problems in classical computing, among which secure multi-party computational geometry (SMCG) is also a direction worthy of research. In 2001, Atallah provided the first definition study of geometric problems for safe calculation of numbers, including point inclusion problems, intersection problems and convex hull problems, and proposed solutions to some of these problems. Subsequent scholars also studied these SMCG problems, such as point inclusion problems, geometric intersection problems, nearest point or point pair problems, solving convex hull problems, etc.
However, solutions to the above problems are limited by computational complexity. Due to the emergence of quantum algorithms, such as Shor's algorithm and Grover's algorithm, these security algorithms based on computational complexity will face threats. Therefore, it is necessary to study secure multi-party computational geometry based on quantum mechanics. Shi et al. proposed an arbitrary region privacy-preserving point inclusion protocol based on phase-encoded quantum private queries in 2016. In 2017, Peng et al. also solved the two-party distance solution problem using phase-encoded quantum privacy query. Soon after, Chen et al. published a paper pointing out the security shortcomings of Peng's solution, analyzing the reasons for the shortcomings of the original solution, and proposing a new solution. In 2018, Peng et al. proposed a quantum protocol for secure two-party distance calculation using QKD-based quantum private queries. In an article published in 2019, Liu et al. proposed a protocol based on oracle and quantum counting algorithm to handle the geometric intersection problem of two parties, but this method is limited to the participation of two parties and cannot be well extended to the case of multiple parties. .
In this paper, the authors pioneer the use of quantum homomorphic encryption to solve the multi-square convex hull problem. Two or more users have their own point sets. The purpose of the author's agreement is how to find the common convex hull of all user point sets without revealing the user's own information. The information of the convex hull points is known to everyone. A value comparison protocol based on quantum homomorphic encryption is proposed to ensure the security of data values. This protocol is then applied to the convex hull calculation protocol, and finally the solution of the protocol is obtained.

basic knowledge

Quantum homomorphic encryption

The problem solved by the QHE solution is that after the data is encrypted, after homomorphic evaluation, the final decryption result is the same as the same calculation result of the original plaintext, which can solve the security calculation problem. The QHE scheme consists of four algorithms (key generation, encryption algorithm, evaluation algorithm, decryption algorithm).

1. The key generation algorithm will randomly generate an encryption key ek and a decryption key dk. Calculate dk according to the given ek algorithm
2. The encryption algorithm ε encrypts the quantum state σ and outputs the encrypted quantum state $E_{}(ek,d)$
3. The evaluation algorithm is to encrypt data $\epsilon (ek,\delta )$ performs quantum calculation U, and after execution, the final ciphertextE ε ( ek , δ ) E_ε(ek, δ)$is\; obtained$$E_{}(ek,\delta )$
4. 解密结果D对$E_e^{\prime }(ek,\delta )$时间解密，流定明文$p^{\prime }=D(dk,E_e^{\prime }(ek,\sigma ))$ ,$p^{\prime }=U\sigma U^{†}$
   In this paper, we use X gates and Z gates for plaintext qubits$\sigma$ is encrypted and proven to be completely secure by Boykin et al.
   In key generation, quantum gate operations can be performed on the original ciphertext, and the original key ek generates the final decryption key dk according to the key update algorithm. Each execution of the quantum gate is called$G_i(i=1,2\dots k,kis\; the\; total\; number\; of\; executions)$ , each quantum gate is a set$S=${ $X,Y,Z,H,S,T,$An element of$CNOT\; \}.$The key update algorithm has the following situations: If Gi = X or Y or Z, assuming it acts on the m-th bit of ek, the key value of the i-th step of the key update algorithm remains unchanged. As shown in equation (1),
   
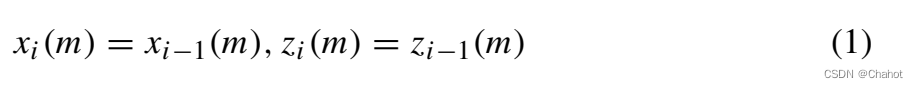
   if Gi = H, assuming it acts on the m-th bit of ek, the key value of the i-th step of the key update algorithm follows equation (2).
   
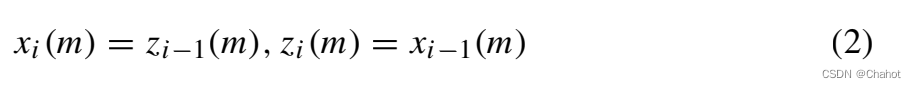
   If Gi = S, assume that it acts on the m-th bit of ek, then the key value of the i-th step of the key update algorithm follows formula (3)
   
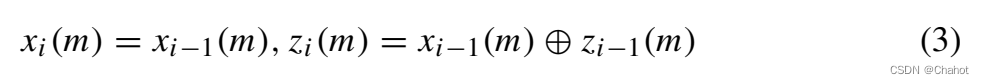
   If Gi = S, assume that it acts on the m-th and l-th bits of ek , then the key value of step i of the key update algorithm follows Equation (4).
   
   If Gi = T, an s error occurs due to executing the T gate for evaluation. Then there is an error of$T{X}^x{Z}^z|\psi ⟩=X^x{Z}^x{S}^{x}T|\psi .$_ In order to eliminate the s error, Gao et al. designed a T-gate process quantum circuit based on Sx rotating Bell measurement, as shown in Figure 1. After executing this circuit, we can get ra and rb, then$T{X}^{x\oplus z}{S}^x{Z}^z|\psi ⟩=X^{x\oplus r_a}{Z}^{x\oplus z\oplus r_b}T|\psi$　 .$\_$
   
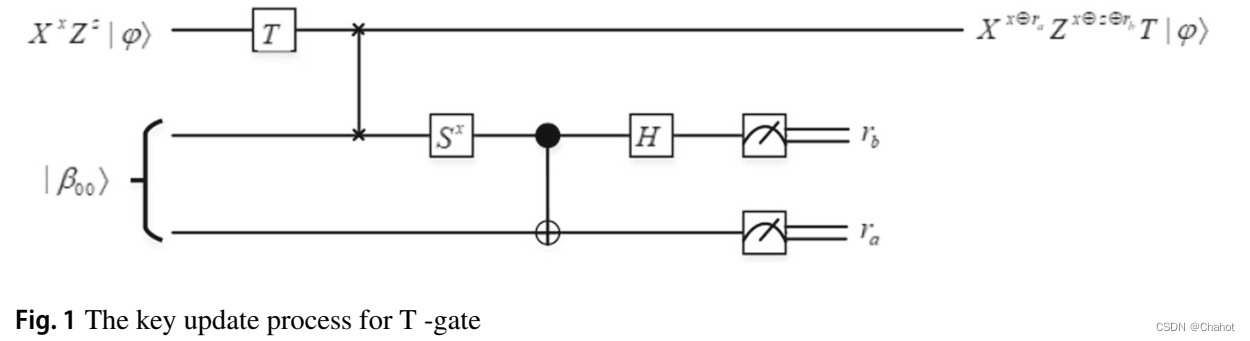
   Assuming that Gi = T acts on the mth bit of ek, the key value of the i-th step of the key update algorithm follows formula (5).
   

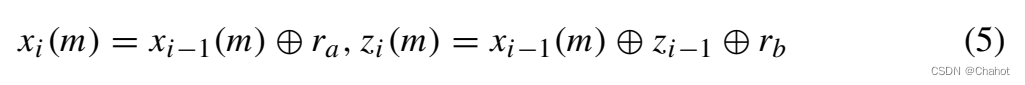
Quantum logic gates and quantum subtraction circuits

Logic gate circuits are the basis of quantum computing. Single qubit gates include Pauli operations X, Y, Z, Hadamard gate H and phase gates T, S. The quantum subtractor is designed to obtain subtraction information from n two binary numbers a and b. In this article, we use the quantum subtractor designed by Yuan. The specific idea is: first start subtracting from the lowest bit, then consider whether it needs to borrow from the upper bits, and then subtract the second bit until the last bit. To reuse constant inputs, use a reset operation to set the constant inputs to 0, which can significantly reduce the number of constant inputs. The qubit input subtraction circuit is shown in the figure.

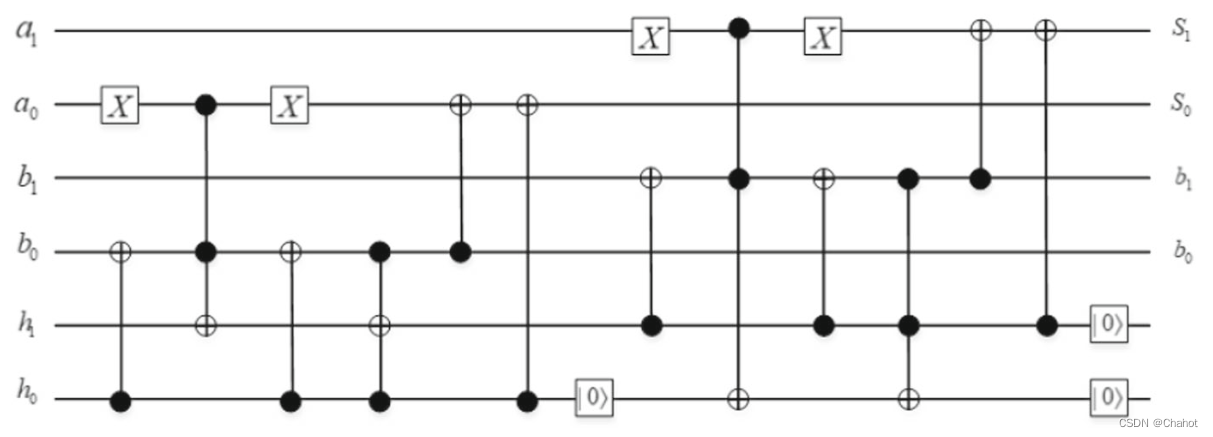
Value Comparison Protocol (VCP_QHE) based on homomorphic encryption

This section introduces a private comparison protocol based on quantum homomorphic encryption that securely protects value comparisons between two parties. Participants include Alice, Bob (two information owners) and a semi-trusted third party. We can divide the semi-trusted third party into a computing center and a key distribution center. The computing center is only responsible for message calculation, while the semi-trusted key center is responsible for key distribution. In our protocol, we use horizontal polarization and vertical polarization to represent point information, with horizontally polarized photon |1> representing binary message 1 and vertically polarized photon |0> representing binary message 0. Alice and Bob respectively send the encrypted information to the quantum circuit U in the computing center for calculation. A quantum circuit U contains a number of logic gates that belong to the set S = {X, Y, Z, H, S, T, CNOT}. The protocol flow chart is shown in Figure 4, and the specific steps are as follows:

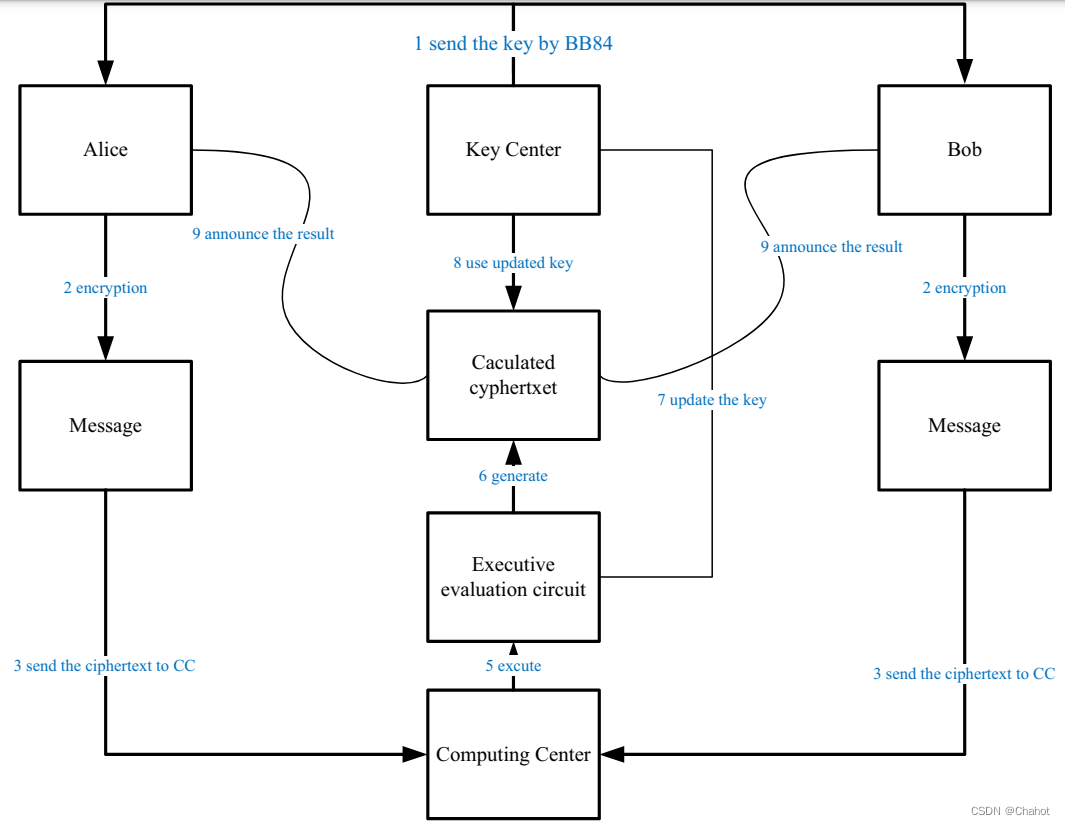
1. The key center randomly generates a key ek = (x0,z0) of length 2n, where x0,z0 belongs to {0,1} ⁿ . ek is then sent to Alice and Bob via the BB84 quantum key distribution protocol.
2. Alice and Bob encode their information respectively, and Alice and Bob use ek to encode the photon sequence $|{\psi }_A⟩=|{\psi }_A^1{p}_A^2{p}_A^3\cdot \cdot \cdot p_A^n⟩$ ,$|{\psi }_B⟩=|{\psi }_B^1{p}_B^2{p}_B^3\cdot \cdot \cdot p_B^n⟩$最作动物，交实密文工作$|{\psi }_A^{\prime }⟩=X^{x_1}{Z}^{z_1}|{\psi }_A^1⟩\otimes X^{x_2}{Z}^{z_2}|{\psi }_A^2⟩\cdot \cdot \cdot \otimes X^{x_n}{Z}^{z_n}|{\psi }_A^n⟩$ ,$|{\psi }_B^{\prime }⟩=X^{x_1}{Z}^{z_1}|{\psi }_B^1⟩\otimes X^{x_2}{Z}^{z_2}|{\psi }_B^2⟩\cdot \cdot \cdot \otimes X^{x_n}{Z}^{z_n}|{\psi }_B^n.$ _ These ciphertext sequences need to be sent to the computing center for execution and are prepared in advance. In order to prevent third-party eavesdropping, Alice and Bob prepared some decoy photons, each photon from∣ 10 ⟩ ∣ 11 ⟩ ∣ + ⟩ ∣ − ⟩ |10\rangle|11\rangle |+\rangle |-\rangleChoose from$|10$$|$$|11$$|$$|$$+$$|$$|$$-$$|\; .$These decoy photons will be randomly inserted. After completing this operation, the new sequence will be sent to the computing center.
3. After the computing center receives the encrypted sequence sent by Alice and Bob, Alice and Bob announce the insertion position of the decoy photon and the corresponding measurement base. If the inserted decoy is |0> or |1>, the measurement base is |0> or | 1>, [1}}; If the inserted bait is |+> or |->, the measurement base is |+> or |->. The calculation center performs the sorting based on the information provided. If the measurement results do not reach the threshold set by Alice and Bob, the protocol will terminate. Otherwise, the calculation center discards the decoy photons and obtains the original encrypted sequence $|{\psi }_A^{\prime }⟩$和$|{\psi }_B^{\prime }.$ _ In order to make the bit length of the input calculation consistent, the calculation center adds I0 > in front of the encrypted sequence with a shorter sequence length before calculation, so that the lengths of the two sequences are consistent.
4. The computing center builds a quantum subtraction circuit and takes two encrypted sequences as circuit inputs. At the same time, the key center updates the original key cycle based on the quantum logic gates executed by the computing center. Suppose we set each execution of the quantum logic gate in the circuit as Gi, and execute K times in total, then the final ciphertext result can be expressed as $G_k(G_{k-1}(\cdot \cdot \cdot (G2(G1(|{\psi }_A^{\prime }⟩,|{\psi }_B^{\prime }⟩)))\cdot \cdot \cdot ))$ . The decryption key is$dk=(xk,zk)$ , the key update rules will be explained later. Finally, the calculation center sends the calculation results to the key center.
5. After receiving the result, the key center uses the decryption key dk to decrypt and measure it, and finally obtains the information (calculation result) subtracted by Alice and Bob.
6. The key center announces the final result to Alice and Bob, and the agreement ends.

Secure multi-party convex hull protocol based on VCP_QHE

Suppose there are multiple users Ui(i>1), each user has his own point set set _i , and he wants to solve the common convex hull Σset _i of the point set . But they don't want the other party to know their own information, only the information on the convex hull. The current security protocols proposed by classical parties are based on computational complexity, and the problems of such protocols are threatened by quantum computing. In order to describe this process more clearly, this paper describes the two-party secure convex hull protocol, and finally extends it to the secure multi-party convex hull protocol. In a two-party protocol, assume our participants are Alice and Bob, and a semi-trusted third party. Alice has a private point set S _A = (p1, p2, p3..., pm), and Bob has a private point set S _B = (q1, q2, q3...qn). Alice and Bob need to calculate the convex hull of m + n points without revealing information about their own point sets. Specific steps are as follows:

Step 1 Alice and Bob respectively calculate the smallest points pA min∈S _A and qB min∈S _B in the y-axis coordinates (note that you can also choose the maximum value on the y-axis or the minimum and maximum value on the x-axis, as long as the required points It is the extreme point in the current set).
Step 2 Alice and Bob use VCP_QHE to compare the values ​​of their extreme points pA min and qB min.
If pA min > qB min, then qB min is an extremum point of the m + n set and a point on the convex hull. Generate a horizontal unit vector in the x-axis direction through qB min → v0v1 (v0 is a point on the vector, v1 = qB min).
If pA min < pbmin, then pA min is an extreme point of the m + n set and also a point on the convex hull. Generate a horizontal unit vector in the x-axis direction through pA min→v0v1 (v0 is a point on the vector, v1 = pA min).
If pA min = qB min, then pA min and qB min are both the extreme points of the m + n set and two points on the convex hull. The vector → v0v1, v0 = pA min, v1 = qB min is generated by pA min and qB min.
Step 3 Alice calculates the cosine value $co{s}_l(l=1,2，\dots ,m)$的$\overrightarrow{v_i{p}_l}$和$\overrightarrow{v_{i-1}{v}_i}$(i represents the i-th convex hull point, l=1,2,3...m), and select its maximum cosine value cos A. At the same time, Bob calculates the cosine value cos _{t (t =1,2,...),} viqt of n) → \overrightarrow {v_iq_t}$\overrightarrow{v_i{q}_t}$和$\overrightarrow{v_{i-1}{v}_i}$, and then select its maximum cosine value cos B.
Step 4 Alice and Bob compare $bodyA(body<\overrightarrow{v_i{p}_{max}},\overrightarrow{v_{i-1}{v}_i}>)$和$cosB(cos<\overrightarrow{v_i{p}_{max}},\overrightarrow{v_{i-1}{v}_i}>)$ size. p max and q max are the points with the largest cosine values ​​in Alice's and Bob's point sets respectively. The comparison results will be in three situations:
if cos A>cos B, then pmax is a convex hull point, assuming p max→v_i+1. Loop steps 3 and 4 until v_i+1≡v₁, where the last bump is the first bump, and then the protocol ends. If cos A<cos B, then q max is a convex hull point, and let q max→vi+1. Loop steps 3 and 4 until vi+1≡v1, where the last bump is the first bump, and then the protocol ends. If cos A=cos B.
Step 5Alice and Bob calculate the distances disA and disB from the convex hull point vi to p max and q max respectively, and then compare these two distances through VCP_QHE. If not. disB, then set p max→vi+1, otherwise set q max→vi+1. Repeat steps 3 and 4 until vi+1≡v1, where the last bump is the first bump, and the protocol ends.

Since the whole process of the protocol solution is to obtain the next convex hull point based on the previous convex hull point, we can know that two convex hull points can form the sides of a convex hull, so every two convex hull points obtained will form a convex hull. The set of all edges is a complete convex hull. The resulting set of points represents the convex hull of the entire set of points (i.e., the closed loop formed by the straight line according to the order of the points obtained is the convex hull).
Based on the above secure two-party convex hull protocol, we can also extend it to secure multi-party convex hull computation. The process of the multi-user U _i (i = 1,2,3...,n) protocol is roughly the same as the process of the two-party convex hull protocol. In step 1, U _i get its own extreme points respectively, and then use the VCP_QHE protocol to finally get an extreme point Σ Si (the set of all points); VCP_QHE is also used to solve the maximum cosine value in step 3 and the maximum cosine value in step 5. the maximum distance. Since the VCP_QHE we designed is solved by both parties, we need to make pairwise judgments on the inputs of multiple users. Finally, after loop judgment, each user Ui can obtain the convex hull of all points.

Accuracy analysis

In this section, we perform a use case analysis of VCP_QHE and the secure multi-party convex hull protocol. First, we analyze the VCP_QHE protocol, assuming that Alice has data I _A = 58, Bob has data I _B = 30, and encode them into binary respectively, and get I _A = (1,1,1,0,1,0) and I _B =(1,1,1,1,0). Since the lengths of I _A and I _B are inconsistent, we add |0> in front of the smaller I to get I' _B = (0,1,1,1,1,0), which has the same length. Through the calculation of the computing center (ie I _A − I _B ) and the decryption of the key center (ie I _res = (1,1,1,0,0) > 0, we can know that I _A > I _B .

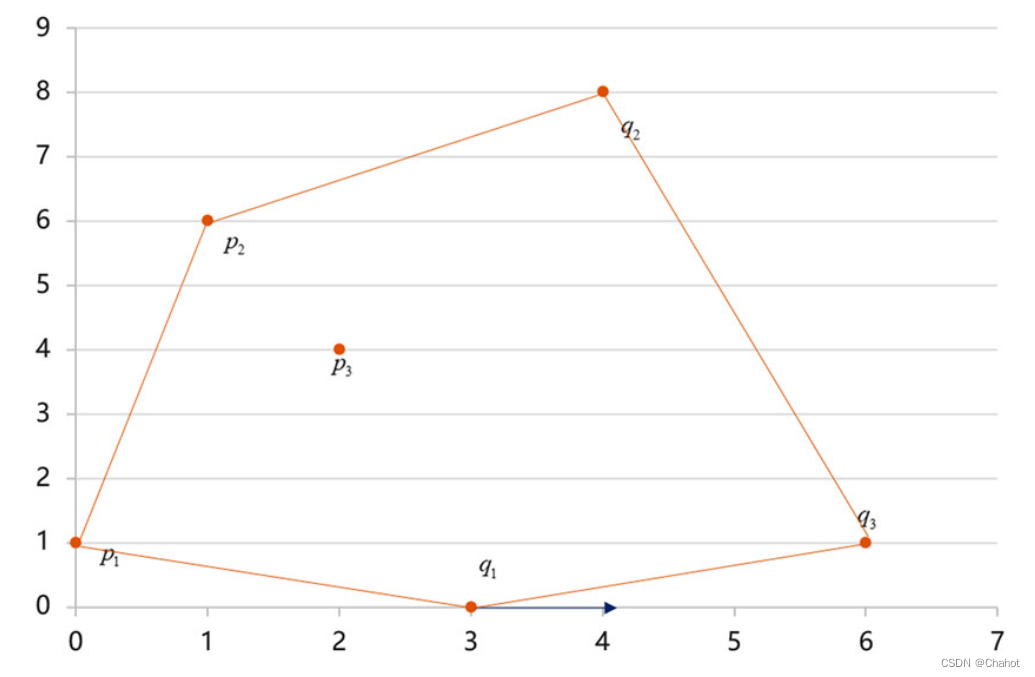
Through the VCP_QHE protocol Judging cos A and cos B, it is concluded that cos A<cos B, so the new convex hull point is q3. Then use q3 as the base point to get the subsequent convex hull point. The process is q1→q3→q2→p2→p1→ q1, as shown in the figure above.
For the correctness analysis of secure polygonal convex hull, we assume that Alice and Bob have point sets S _A = {(0,1), (1,6), (2,4)}, S _B={(3,0), (4,8), (6,1)}, as shown in the figure. Alice and Bob compute the smallest y-coordinates in their set of points, labeled p1 and q1 respectively. By applying the VCP_QHE protocol to p1 and q1, it can be seen that q1 is the smallest point along the y-axis direction in the entire set, and it is also the first convex hull point. According to q1, the maximum cosine values ​​of Alice and Bob are respectively obtained as shown in Equation 6 and Equation 7.

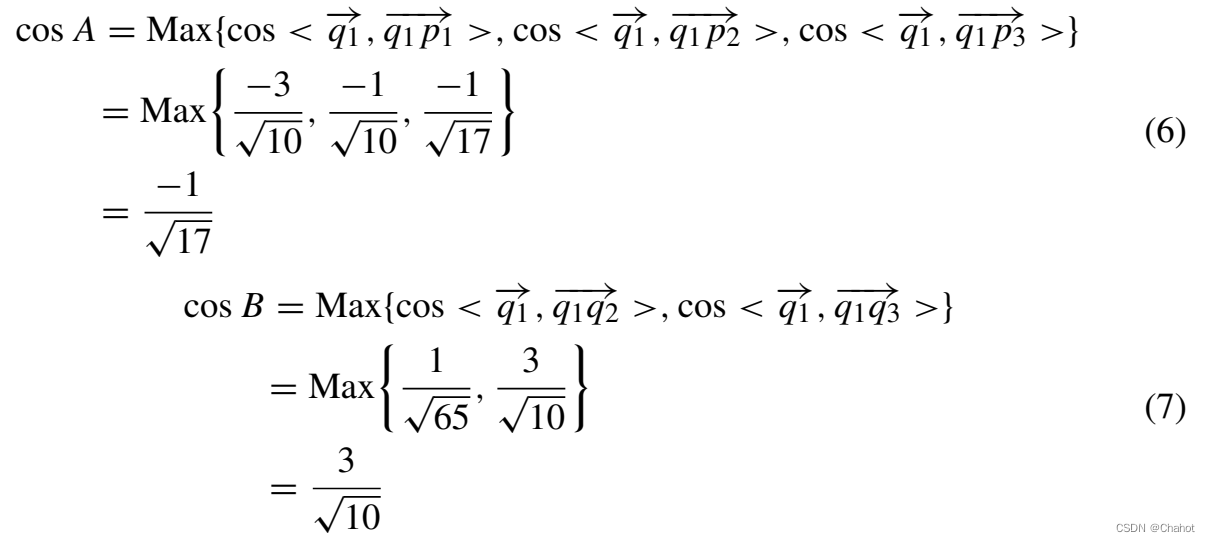
Without loss of generality, it is assumed that there are n users U1 U2 . . . , each user contains its own point information. Each user calculates the extreme points in his own point set Ei, compares Ei through the VCP_QHE protocol, and obtains the first convex hull point C1. Ui calculates the minimum cosine value $cos<C_1,C_1{P}_k{>}_i$From the horizontal vector $C_1{P}_k$composition. Then compare and get the minimum cosine value $cos<C_1,C_1{P}_k{>}_i$And cos < C 1 , C 1 P k > i cos<C_1,C_1P_k>_i in the entire point set$cos<C_1,C_1{P}_k{>}_i$. That is, the second convex hull point C2 can be obtained. Therefore, each user first finds the minimum cosine value formed by its own point and the convex hull edge C _i−2 C _{i−1 , and then compares the cosine value through the secure VCP_QHE protocol.} When obtaining the value of the next convex hull point Ci, the information of the first convex hull point is the same. Then solve all convex hull points, all convex hull points C1C2...Cm. The whole solution process is completely correct, and the security also benefits from the guarantee of homomorphic encryption.

Security analysis

Since we are the first to use quantum homomorphic encryption to solve the convex hull problem, there are no other protocols to which we can compare. We can only analyze the security of the proposed protocol from the following perspectives.

Data and key security

Since the initial encryption key ek is randomly generated by the key center using the secure key generation algorithm QOTP, the security of the generated initial key can be guaranteed. In the key update algorithm, when the key center interacts with the computing center, the computing center only provides the quantum logic gates executed at each step, so the (x, z) intermediate key and the final dk are safe during the key update process . In terms of data security, since the initial key and decryption key are owned by the key center, the possibility of data eavesdropping by the key center is high. However, in our protocol, this is not feasible, because the user encrypts the data through the initial key ek distributed by the key center, and then directly transmits it to the computing center through a secure quantum channel. After the gate circuit is completed, the obtained data will be sent to the key center for decryption. Therefore, the key center can only obtain the manipulated data information, but cannot obtain the original plaintext information. So the data is safe.

external attack

External attackers can attack during key distribution, ciphertext transmission, and homomorphic evaluation. During the key distribution process, the keys are distributed using the BB84 protocol, so external attackers cannot obtain the keys. During the transmission of ciphertext, external attackers may attack the quantum channel to obtain data. However, before data transmission, users randomly add decoy photons to the encrypted photon sequence. Therefore, even if an attacker intercepts the ciphertext message, he has no way of knowing what the original message was. During the homomorphic evaluation, the communication between the computing and the key center is carried out through quantum channels, and decoy photons are inserted in the information to prevent eavesdropping, so it is also safe.

insider attack

In this case, our protocol is also completely safe if N dishonest participants want to steal other people's information. Since semi-trusted key centers and computing centers must be faithful to the implementation process and cannot cooperate with other participants or third parties, they can only infer other people's information from the information they have obtained. We described the security of user data in the previous section. Therefore, the key center and computing center cannot obtain the real information of other users. On the other hand, since the final results announced by the key center do not publish specific differences, users cannot obtain information from other parties through the difference data, nor can they cooperate with other participants to obtain users' real data. So our protocol is resistant to attacks by participants.