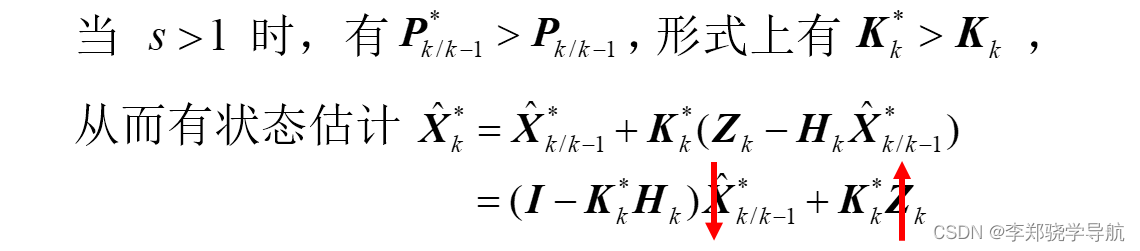函数模型
{ X k = Φ k l k − 1 X k − 1 + Γ k − 1 W k − 1 Z k = H k X k + V k \left\{\begin{array}{l} \boldsymbol{X}_{k}=\boldsymbol{\Phi}_{k l k-1} \boldsymbol{X}_{k-1}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{W}_{k-1} \\ \boldsymbol{Z}_{k}=\boldsymbol{H}_{k} \boldsymbol{X}_{k}+\boldsymbol{V}_{k} \end{array}\right. {
Xk=Phik l k − 1Xk−1+Ck−1Wk−1Zk=HkXk+Vk
随机模型
{ E [ W k ] = 0 , E [ W k W j T ] = s N − k + 1 Q k δ k j j , k ≤ N E [ V k ] = 0 , E [ V k V j T ] = s N − k R k δ k j E [ W k V j T ] = 0 \left\{\begin{array}{ll}\mathrm{E}\left[\boldsymbol{W}_{k}\right]=\mathbf{0}, & \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{W}_{j}^{\mathrm{T}}\right]={\color{green}s^{N-k+1}}\boldsymbol{Q}_{k} \delta_{k j}\quad j,k \le N\\ \mathrm{E}\left[\boldsymbol{V}_{k}\right]=\mathbf{0}, & \mathrm{E}\left[\boldsymbol{V}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]={\color{green}s^{N-k}} \boldsymbol{R}_{k} \delta_{k j} \quad \\ \mathrm{E}\left[\boldsymbol{W}_{k} \boldsymbol{V}_{j}^{\mathrm{T}}\right]=\mathbf{0}\end{array}\right. ⎩
⎨
⎧E[Wk]=0,E[Vk]=0,E[WkVjT]=0E[WkWjT]=sN − k + 1 Qkdkjj,k≤NE[VkVjT]=sN − k Rkdkj
Where: fading factor s ≥ 1 s \ge 1s≥1 , equal to1 11 is the same as ordinary Kalman filtering. Now it isNNN moment,kkThe smaller k is the more previous,s N − ks^{Nk}sThe larger N − k , the larger the coefficient multiplied in front of the noise, the more unreliable the previous measurement and system, and slowly forget;k = N k = Nk=N is now, at this times N − ks^{Nk}sN − k is1 11。
added ssAfter s , the model still satisfies the Kalman filtering condition, and the noise is still Gaussian white noise, but the time changes. InNNThe Kalman filter at time N is as follows, in fact, there are moresss :
{ X ^ k / k − 1 N = Φ k / k − 1 X ^ k − 1 N P k / k − 1 N = Φ k / k − 1 P k − 1 N Φ k / k − 1 T + Γ k − 1 s N − k Q k − 1 Γ k − 1 T K k N = P k / k − 1 N H k T ( H k P k / k − 1 N H k T + s N − k R k ) − 1 X ^ k N = X ^ k / k − 1 N + K k N ( Z k − H k X ^ k / k − 1 N ) P k N = ( I − K k N H k ) P k / k − 1 N \left\{\begin{array}{l}\hat{\boldsymbol{X}}_{k / k-1}^{N}=\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}^{N} \\ \boldsymbol{P}_{k / k-1}^{N}=\boldsymbol{\Phi}_{k / k-1} \boldsymbol{P}_{k-1}^{N} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} {\color{green}s^{N-k}}\boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{N}=\boldsymbol{P}_{k / k-1}^{N} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}^{N} \boldsymbol{H}_{k}^{\mathrm{T}}+{\color{green}s^{N-k}} \boldsymbol{R}_{k}\right)^{-1} \\ \hat{\boldsymbol{X}}_{k}^{N}=\hat{\boldsymbol{X}}_{k / k-1}^{N}+\boldsymbol{K}_{k}^{N}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}^{N}\right) \\ \boldsymbol{P}_{k}^{N}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{N} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}^{N}\end{array}\right. ⎩
⎨
⎧X^k/k−1N=Phik/k−1X^k−1NPk/k−1N=Phik/k−1Pk−1NPhik/k−1T+Ck−1sN − k Qk−1Ck−1TKkN=Pk/k−1NHkT(HkPk/k−1NHkT+sN − k Rk)−1X^kN=X^k/k−1N+KkN(Zk−HkX^k/k−1N)PkN=(I−KkNHk)Pk/k−1N
Gain Calculation Loop Rewrite
Extract s N ks^{N_k}sNk
s − ( N − k ) P k / k − 1 N = Φ k / k − 1 s ⋅ s − [ N − ( k − 1 ) ] P k − 1 N Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T K k N = s − ( N − k ) P k ∣ k − 1 N H k T ( H k s − ( N − k ) P k k k − 1 N H k T + R k ) − 1 s − ( N − k ) P k N = ( I − K k N H k ) s − ( N − k ) P k ∣ k − 1 N \begin{array}{l} {\color{red}s^{-(N-k)} \boldsymbol{P}_{k / k-1}^{N}}=\boldsymbol{\Phi}_{k / k-1} {\color{green}s} \cdot {\color{red}s^{-[N-(k-1)]} \boldsymbol{P}_{k-1}^{N}} \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{N}={\color{red}s^{-(N-k)} \boldsymbol{P}_{k \mid k-1}^{N}}\boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} {\color{red}s^{-(N-k)} \boldsymbol{P}_{k k k-1}^{N}} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ {\color{red}{s^{-(N-k)} \boldsymbol{P}_{k}^{N}}}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{N} \boldsymbol{H}_{k}\right) s^{-(N-k)} \boldsymbol{P}_{k \mid k-1}^{N} \\ \end{array} s−(N−k)Pk/k−1N=Phik/k−1s⋅s−[N−(k−1)]Pk−1NPhik/k−1T+Ck−1Qk−1Ck−1TKkN=s−(N−k)Pk∣k−1NHkT(Hks−(N−k)Pkkk−1NHkT+Rk)−1s−(N−k)PkN=(I−KkNHk)s−(N−k)Pk∣k−1N
Merge the red parts: Let P k ∗ ≜ s − ( N − k ) P k N , P k / k − 1 ∗ ≜ s − ( N − k ) P k / k − 1 N \boldsymbol{P}_{ k}^{*} \triangleq s^{-(Nk)} \boldsymbol{P}_{k}^{N}, \boldsymbol{P}_{k / k-1}^{*} \triangleq s ^{-(Nk)} \boldsymbol{P}_{k / k-1}^{N}Pk∗≜s−(N−k)PkN,Pk/k−1∗≜s−(N−k)Pk/k−1N,have to
{ X ^ k / k − 1 ∗ = Φ k / k − 1 X ^ k − 1 ∗ P k / k − 1 ∗ = Φ k / k − 1 ( s P k − 1 ∗ ) Φ k / k − 1 T + Γ k − 1 Q k − 1 Γ k − 1 T K k ∗ = P k / k − 1 ∗ H k T ( H k P k / k − 1 ∗ H k T + R k ) − 1 X ^ k ∗ = X ^ k / k − 1 ∗ + K k ∗ ( Z k − H k X ^ k / k − 1 ∗ ) P k ∗ = ( I − K k ∗ H k ) P k / k − 1 ∗ \left\{\begin{array}{l}\hat{\boldsymbol{X}}_{k / k-1}^{*}=\boldsymbol{\Phi}_{k / k-1} \hat{\boldsymbol{X}}_{k-1}^{*} \\ \boldsymbol{P}_{k / k-1}^{*}=\boldsymbol{\Phi}_{k / k-1}\left({\color{green}s} \boldsymbol{P}_{k-1}^{*}\right) \boldsymbol{\Phi}_{k / k-1}^{\mathrm{T}}+\boldsymbol{\Gamma}_{k-1} \boldsymbol{Q}_{k-1} \boldsymbol{\Gamma}_{k-1}^{\mathrm{T}} \\ \boldsymbol{K}_{k}^{*}=\boldsymbol{P}_{k / k-1}^{*} \boldsymbol{H}_{k}^{\mathrm{T}}\left(\boldsymbol{H}_{k} \boldsymbol{P}_{k / k-1}^{*} \boldsymbol{H}_{k}^{\mathrm{T}}+\boldsymbol{R}_{k}\right)^{-1} \\ \hat{\boldsymbol{X}}_{k}^{*}=\hat{\boldsymbol{X}}_{k / k-1}^{*}+\boldsymbol{K}_{k}^{*}\left(\boldsymbol{Z}_{k}-\boldsymbol{H}_{k} \hat{\boldsymbol{X}}_{k / k-1}^{*}\right) \\ \boldsymbol{P}_{k}^{*}=\left(\boldsymbol{I}-\boldsymbol{K}_{k}^{*} \boldsymbol{H}_{k}\right) \boldsymbol{P}_{k / k-1}^{*}\end{array}\right. ⎩
⎨
⎧X^k/k−1∗=Phik/k−1X^k−1∗Pk/k−1∗=Phik/k−1(sPk−1∗)Phik/k−1T+Ck−1Qk−1Ck−1TKk∗=Pk/k−1∗HkT(HkPk/k−1∗HkT+Rk)−1X^k∗=X^k/k−1∗+Kk∗(Zk−HkX^k/k−1∗)Pk∗=(I−Kk∗Hk)Pk/k−1∗
There is only one ss in the rewritten formulas , it is very simple to use, for the PPat the last momentP matrix multiplied by a scalarsss will do.
Understanding the effect of forgetting
s s The larger the value of s , the smaller the utilization of previous information