I. Introduction

The subject is reviewing the course "Mathematical Analysis and Modeling" recently. When reviewing the graph theory part, he came into contact with Dijkstra's algorithm and Floyd, two classic algorithms used to solve the shortest path. When understanding Floyd's algorithm, he consulted a lot of other people's understanding. Finally, he probably understood the working process of this algorithm. I wrote down my understanding as a record, hoping to help the latecomers.

Two, Floyd algorithm workflow analysis

Unlike Dijkstra's algorithm, Floyd's algorithm is used to solve the shortest path problem between two points. It works as follows:

(1) Construct the initial path example matrix $D^{(0)}_{n\times n}$ , route matrix $P^{(0)}_{n\times n}$

Here is a direct reference to the shortest path problem in https://blog.csdn.net/qq_42518956/article/details/116705635 , the picture is the initial problem inside

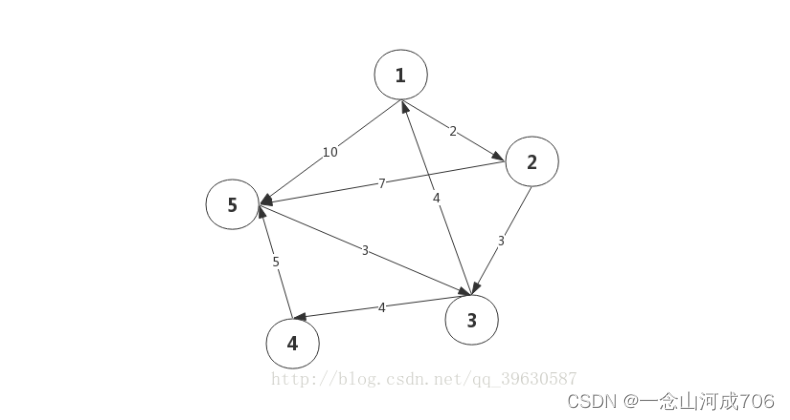
So we first construct a $\times$ distance matrix between two points of 5 5, $d^{(0)}_{ij}$ indicating the distance from point i to point j, the distance matrix is as follows:

tip: due to negligence, here I regard the two points as two-way

$D^{(0)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&\infty&10\\ 2&0&3&\infty&7\\ 4&3&0&4&3\\ \infty&\infty&4&0&5\\ 10&7&3&5&0\\ \end{bmatrix}$

The initial path matrix is:

$P^{(0)}_{5\times5}$ = $\begin{bmatrix} 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ \end{bmatrix}$ , each line is from 1 to the last point

(2) The key process of Floyd's algorithm is to insert points sequentially from the first point to the last point. When inserting the kth point, make $d^{(k)}_{ij}$ $=min\left\{d^{(k-1)}_{ij},d^{k-1}_{ik}+d^{k-1}_{kj}\right\}$ , $d^{(k)}_{ij}\neq d^{(k-1)}_{ij}$ at that time , correct the corresponding position in the path, and replace the value there with k.

First, do the first point insertion and calculate d1(i,j)= $d^{k-1}_{ik}+d^{k-1}_{kj}$ , the calculation result is as follows:

Compare the value of each item of d1 with $d^{(0)}_{ij}$ and select a smaller value as $d^{(1)}_{ij}$ the first interpolation value. The original value is not greater than the value in d1, and the result is $D^{(1)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&\infty&10\\ 2&0&3&\infty&7\\ 4&3&0&4&3\\ \infty&\infty&4&0&5\\ 10&7&3&5&0\\ \end{bmatrix}$ $P^{(1)}_{5\times5}$ = $\begin{bmatrix} 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ \end{bmatrix}$

Carry out the second point insertion and calculate d2(i,j)= $d^{(1)}_{i2}+d^{(1)}_{2j}$ , the calculation result is as follows:

The red part has a smaller value: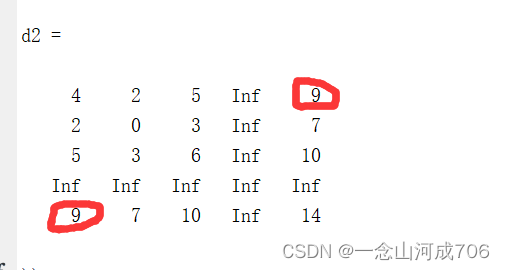

Then change the distance matrix $D^{(2)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&\infty&9\\ 2&0&3&\infty&7\\ 4&3&0&4&3\\ \infty&\infty&4&0&5\\ 9&7&3&5&0\\ \end{bmatrix}$ , the route matrix is $P^{(2)}_{5\times5}$ = $\begin{bmatrix} 1&2&3&4&2\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 1&2&3&4&5\\ 2&2&3&4&5\\ \end{bmatrix}$

Carry out the third point insertion, $d3=d^{(2)}_{i3}+d^{(2)}_{3j}$ , the result is as follows

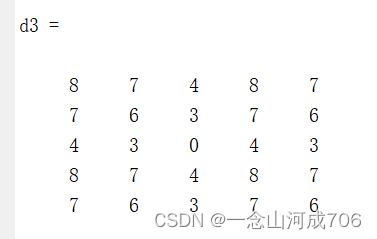
For value comparison, the red part is smaller:

Then $D^{(3)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&8&7\\ 2&0&3&7&6\\ 4&3&0&4&3\\ 8&7&4&0&5\\ 7&6&3&5&0\\ \end{bmatrix}$ , the route matrix $P^{(3)}_{5\times5}$ $=\begin{bmatrix} 1&2&3&3&3\\ 1&2&3&3&3\\ 1&2&3&4&5\\ 3&3&3&4&5\\ 3&3&3&4&5\\ \end{bmatrix}$

Carry out the fourth point insertion, $d4=d^{(3)}_{i4}+d^{(3)}_{4j}$ , the result is as follows

The matrix does not change, $D^{(4)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&8&7\\ 2&0&3&7&6\\ 4&3&0&4&3\\ 8&7&4&0&5\\ 7&6&3&5&0\\ \end{bmatrix}$ , $P^{(4)}_{5\times5}$ $=\begin{bmatrix} 1&2&3&3&3\\ 1&2&3&3&3\\ 1&2&3&4&5\\ 3&3&3&4&5\\ 3&3&3&4&5\\ \end{bmatrix}$

Carry out the fifth point insertion, the process is the same as before, and the obtained matrix is as follows:

The values are not very good, the matrix remains unchanged.

$D^{(5)}_{5\times5}=$ $\begin{bmatrix} 0&2&4&8&7\\ 2&0&3&7&6\\ 4&3&0&4&3\\ 8&7&4&0&5\\ 7&6&3&5&0\\ \end{bmatrix}$ ， $P^{(5)}_{5\times5}$ $=\begin{bmatrix} 1&2&3&3&3\\ 1&2&3&3&3\\ 1&2&3&4&5\\ 3&3&3&4&5\\ 3&3&3&4&5\\ \end{bmatrix}$

So we get the final distance matrix and route matrix, for example, we find the shortest path from point 1 to point 4, , $D^{(5)}_{14}=8,P^{(5)}_{14}=3$ which means the path is 1->3->4, and the distance is 8.

Three, Floyd algorithm Matlab simple implementation process

It is mainly a three-iteration execution, and the initial distance matrix and route matrix in the algorithm are generated according to the previous method.

clc,clear;  %清空工作区和命令行窗口
D0=[];  %初始距离矩阵
P=[];   %路径矩阵
d=[];
m=size(D0);
for n=1:m   %m次迭代
    for i=1:m
        for j=1:m
            d(i,j)=D0(i,n)+D0(n,j);
            if(d(i,j)<D0(i,j))  %判断值的大小
                D0(i,j)=d(i,j);
                P(i,j)=n;
            end
        end
    end
end

4. About the shortest path between two points with more than one point

For example, the interval between 1 and 6 is 4, and neither 1 nor 6 is directly connected to 4. Then we will find the shortest path from 1 to 4 and 4 to 6, and decompose them in turn to get the shortest route.

Floyd algorithm understanding and step-by-step execution analysis

I. Introduction

Two, Floyd algorithm workflow analysis

(1) Construct the initial path example matrix $D^{(0)}_{n\times n}$ , route matrix $P^{(0)}_{n\times n}$

Three, Floyd algorithm Matlab simple implementation process

4. About the shortest path between two points with more than one point

Guess you like

Floyd algorithm understanding and step-by-step execution analysis

I. Introduction

Two, Floyd algorithm workflow analysis

(1) Construct the initial path example matrix , route matrix

(2) The key process of Floyd's algorithm is to insert points sequentially from the first point to the last point. When inserting the kth point, make , at that time , correct the corresponding position in the path, and replace the value there with k.

Three, Floyd algorithm Matlab simple implementation process

4. About the shortest path between two points with more than one point

Guess you like

(1) Construct the initial path example matrix $D^{(0)}_{n\times n}$ , route matrix $P^{(0)}_{n\times n}$