Binary tree
Introduction to Binary Tree Algorithm
Compared with the binary tree search algorithm, the disadvantages of the ordinary loop search algorithm are:

The binary tree algorithm uses the idea of dichotomy, and its operating principle is as follows:
The idea of binary search is very simple. For an "ordered sequence a (sequence must be sorted first)", if you want to find an element x, you can make x first and the middle of a
Comparison of elements:
① If they are equal, it succeeds;
② If it is less than the middle element. Then search in the left half of a;
③ If it is greater than or equal to the middle element, search in the right half of a.
Figure 5-4 is the process of searching for 25 in an ordered sequence, where I, H, Middle respectively represent the current search interval
The left, right and center positions of the

A loop iteration process can be used to continuously update the three indicators of the left and right positions (L, H) and the middle position (Middle) of the interval to find.
Analysis of Binary Tree Algorithm Code Principle

Binary tree program implementation
#include <iostream>
#include <algorithm>
#include <functional>
using namespace std;
int main()
{
int arr[] = { 1,2,3,4,5,6,7,8,9 };
int L = 0, H = sizeof(arr) / sizeof(int), x = 0;
cin >> x;
while (L <= H)
{
int Middle{ (L + H) / 2 };
if (arr[Middle] == x)
{
break;
}
else if (arr[Middle] > x)
{
H = Middle;
}
else if (arr[Middle] < x)
{
L = Middle;
}
}
if (L <= H)
{
cout << "找到了目标值" << endl;
}
else
{
cout << "未找到目标值" << endl;
}
}
Floyd algorithm
Principle analysis of Floyd algorithm
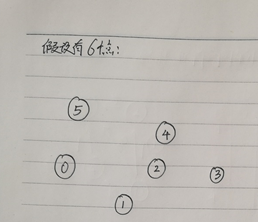
When we want to solve the shortest path ①->⑤, we perform the following operations:
① First establish "5*5 matrix Distance used to store the distance between two points" and "Record the same-dimensional matrix Pointer of the penultimate point"
② We first find out "whether Distance[①,P]+Distance[P,②]<Distance[①,②] with a point of P”, if so, update Distance[①,②]= Distance[①,P]+ Distance[P,②], and update Pointer[①,②]=P;
③ To find this intermediate node, we can use this method to find "Is there a point E makes Distance[①,E] +Distance[E,P]<Distance[①,P]", if it exists, update Distance[①,P ]= Distance[①,E] +Distance[E,P] and Pointer[①,P]=E;
④We continue to subdivide this step by step, until "there is no Y such that Distance[①,Y]+Distance[Y,N]<Distance[①,N]", thus we get the difference between ①->P The shortest path.
⑤ Join the two shortest paths [①,P] and [P,②], we can get the shortest path ①->②, in fact, when we find the bridge P between ①->②, we only need to go further Just analyze the shortest path between ①->P.
How to view the shortest path of the x->y point according to the path matrix Pointer?

We want to understand "the shortest path from 1 (beginning) -> 0 (end)". First, Pointer[1,0]=3, indicating that 1 point, the bridge between the two points 0 is 3 points, we will further analyze The shortest distance between 1 point and 3 points, Pointer[1,3]=2 means 1 point, there is a bridge between 3 points (1->3 the penultimate point of the path) 2 points, and then we further analyze The shortest path between 2 points -> 1 point, Pointer[1,2]=1 When we see that the penultimate point of 1->2 is 1 point (the starting point of the path 1->2), it means "no There is a point that makes the distance between 1->2 smaller than Distance[1,2]".
In the end, we get "a reverse path": 0 (end point)->3->2->1 (start point).
Floyd algorithm code example
#include <iostream>
#include <iomanip>
#include <limits>
using namespace std;
int main()
{
int n = 4;
int INFINITE = INT_MAX;
unsigned int Distance[][4] = { {0,2,6,4},{INFINITE,0,3,INFINITE},{7,INFINITE,0,1},{5,INFINITE,12,0} };
// 初始化路径矩阵
decltype(Distance) Pointer = { 0 };
for (int u = 0; u < n; u++)
{
for (int v = 0; v < n; v++)
{
Pointer[u][v] = u;
}
}
// 显示初始的uv之间的距离与uv路径之间中倒数第二个点
for (int u = 0; u < n; u++)
{
for (int v = 0; v < n; v++)
{
cout << setw(10) << setfill(' ') << Distance[u][v] << ' ';
}
cout << '\n';
}
for (int u = 0; u < n; u++)
{
for (int v = 0; v < n; v++)
{
cout << Pointer[u][v] << ' ';
}
cout << '\n';
}
// Floyd算法
for (int w = 0; w < n; w++)
{
for (int u = 0; u < n; u++)
{
for (int v = 0; v < n; v++)
{
if (w != u && w != v && Distance[u][w] + Distance[w][v] < Distance[u][v] && u != v)
{
Pointer[u][v] = w;
Distance[u][v] = Distance[u][w] + Distance[w][v];
}
}
}
}
// u->v的最短路径
for (int u = 0; u < n; u++)
{
for (int v = 0; v < n; v++)
{
if (u == v) continue;
cout << u << "到" << v << "的逆向路径是:" << v << ',';
for (int w = Pointer[u][v]; w != u; )
{
cout << w << ',';
w = Pointer[u][w];
}
cout << u << " ; " << "其最短距离为" << Distance[u][v] << endl;
}
}
}