1. 剑指 Offer 14- I. 剪绳子
题目描述:给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]…k[m-1] 。请问 k[0]k[1]…*k[m-1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
1.1 方法一:动态规划
1.1.1 推导
- 求最大值问题可考虑使用动态规划算法解决;
- 动态规划解题的四大要素:状态定义、状态转移方程定义、初始状态以及返回结果;
- 针对剪绳子问题,目的是将一个长度为n的绳子划分为m段,m段绳子最大乘积是多少,其中m>1,也就是将绳子需至少划分为两段;
- 动态规划四要素:
1)状态F(i):长度为i的绳子,划分后最大乘积为F(i);
2)状态转移方程:F(i)=Max{F(i),F(i-j)*j,(i-j)*j};
3)初始状态:F(2)=1,长度为2的绳子至少划分为两段,因此每段长度为1;
4)返回结果:F(n),长度为n的绳子划分后的最大乘积; - 长度为n的绳子划分后最大乘积,可由长度小于n的绳子的划分最大乘积进一步得到。假设将绳子划分为两段,一段长度为j,另一段长度为n-j,长度为n-j的绳子可以进一步划分,也可以不划分,因此有对应两种情况:
1)n-j的绳子不再划分,则划分乘积为j*(n-j);
2)n-j的绳子继续划分,则划分乘积为j*F(n-j);
1.1.2 代码实现
class Solution {
// 动态规划
// 状态F(i):长度为i的绳子,划分后最大乘积为F(i)
// 状态转移方程:F(i)=Max{F(i),F(i-j)*j,(i-j)*j}
// 初始状态:F(2)=1
public int cuttingRope(int n) {
int[] maxPro=new int[n+1];
// 初始状态
maxPro[2]=1;
// 状态转移
for(int i=3;i<=n;i++){
for(int j=1;j<i;j++){
maxPro[i]=Math.max(maxPro[i],j*maxPro[i-j]);
maxPro[i]=Math.max(maxPro[i],(i-j)*j);
}
}
// 返回结果
return maxPro[n];
}
}
1.2 方法二:数学规律
1.2.1 数学推导
-
For the problem of cutting the rope, the purpose is to divide a rope of length n into a section, what is the maximum product of the section a rope, where a>1, that is, the rope needs to be divided into at least two sections;
-
Assuming that the rope is divided into a segment, respectively n 1 , n 2 ,..., n a , it can be known from the following arithmetic geometric mean inequality, when n 1 =n 2 =...=n a , n 1 , n 2 ,..., The product of n a is the largest;

-
It can be seen from the above formula that when the rope of length n is divided into equal lengths, the product is the largest. Assuming that the length of each piece of rope is x, and it is divided into a section, the product is x a , a=n/x, further derivation:
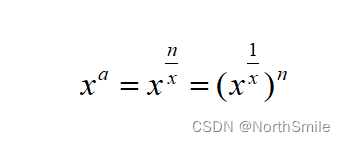
that is, when x 1/x is the largest, the division product is the largest, let y=x 1/x , the implicit function can be derived:

but we know that the length of the rope division needs to be an integer, then the approximate value x=3 or x=2 can be taken, and x is substituted into y=x 1/x respectively, we can know that when x=3, the division product is the largest ; -
Based on the above derivation, the principle of division can be summarized:
1) Divide the rope into segments with a length of 3 as much as possible, a total of t segments, and the remaining length of the rope has three possibilities: 0, 1, and 2; 2)
If the length of the remaining rope is 0, the rope The original length is exactly a multiple of 3, and the optimal solution 3 t is obtained at this time ;
3) If the remaining rope length is 2, the remaining part is regarded as a whole, and no further division is made, and the division product is 3 t *2;
4) If the length of the remaining rope is 1, take out a subsection with a length of 3 and the remaining part with a total length of 4 (divide it into two subsections with a length of 2, because at this time 2*2>1*3), Then the division product is 3 t-1 *2*2;
1.2.2 Code implementation
class Solution {
// 数学推导:将绳子尽可能按照长度为3的段分割,乘积最大
public int cuttingRope(int n) {
if(n<=2){
return 1;
}
// 特殊情况
if(n==3){
return 2;
}
int res=n/3; // 按照3分割,最多得到多少段
int mod=n%3; // 只有0,1,2三种情况
if(mod==0){
return (int)Math.pow(3,res); // 说明是3的倍数
}else if(mod==1){
return (int)Math.pow(3,res-1)*4; // 3a+1,把最后两段3+1划分为2+2
}else{
return (int)Math.pow(3,res)*2; // 3a+2
}
}
}
2. Pointing at Offer 14- II. Cutting the Rope II
Title description: Given a rope of length n, please cut the rope into m segments of integer length (m and n are both integers, n>1 and m>1), and the length of each rope is k[0 ],k[1]…k[m - 1] . What is the maximum possible product of k[0] k[1] ...*k[m - 1]? For example, when the length of the rope is 8, we cut it into three sections whose lengths are 2, 3, and 3 respectively, and the maximum product obtained at this time is 18.
The answer needs to be modulo 1e9+7 (1000000007). If the initial calculation result is: 1000000008, please return 1.
2.1 Derivation
- The basic derivation is shown in Section 1.2.1;
- The difference here from the previous question is that the value range of n becomes larger, so boundary value overflow may occur when calculating 3 t ;
- Based on the nature of the remainder operation as shown in the figure below, the problem of overflowing the value range can be solved by the method of cyclic remainder ;

2.2 Code implementation
class Solution {
public int cuttingRope(int n) {
if(n<=2){
return 1;
}
if(n==3){
return 2;
}
int base=1000000007;
int res=n/3;
int mod=n%3;
if(mod==1){
res-=1;
}
// 计算pow(3,res)
long target=1;
while(res-->0){
target=((target%base)*3)%base;
}
if(mod==0){
return (int)(target%base);
}else if(mod==1){
return (int)((target*4)%base);
}else{
return (int)((target*2)%base);
}
}
}