One of the scenarios that operations research sometimes faces is the problem of finding the shortest path : such as the network design of urban transportation, the surface design of chips, etc. Discrete dynamic programming (DDP) method is commonly used to solve such problems . Today we will learn this scenario and the algorithm to solve it.
1
abstract as model
We introduce the model and related terminology with three examples that closely resemble real-world scenarios.
Littleville Transportation Plan
Suppose you are a traffic engineer in the city of Littleville. The following figure is the urban street plan of the city. The figure shows whether the road is a one-way street or a two-way street, and also marks the average time it takes for a car to pass through each block ( Unit: second).
From survey reports and other data, we can estimate the number of traveling residents, the origin and destination of travel, but it is not known what route they choose. One of the tasks of traffic engineers is to estimate the routes that residents take, so that city managers can estimate whether a certain road will cause congestion.
To get a decent initial estimate, we can first assume that all traveling residents make rational decisions—that is, choose the shortest path connecting origin and destination. Therefore, we first need to find all shortest paths between any two points in the graph.
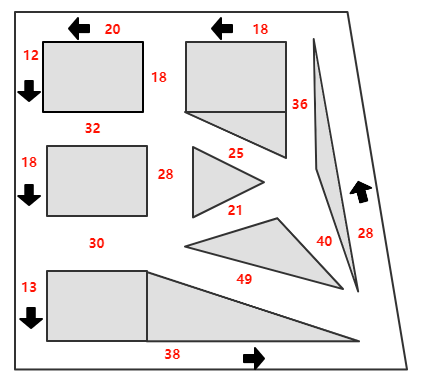
To use mathematics to solve this problem, first, abstract the given block system into a graph or network . We have given a preliminary definition of the graph model in the probability graph of machine learning. In operations research, there are Slightly different, in order to express clearly and precisely, we define:
Nodes represent entities, intersections, and transitions in the network . For convenience, the nodes in the Littleville example are numbered from 1 to 10. Nodes may be connected by arcs or edges ( arcs refer to directional edges ) . For example, arcs are used here to represent one-way streets, and edges are used to represent two-way streets.
The Littleville example, converted to a graph, is represented as follows:
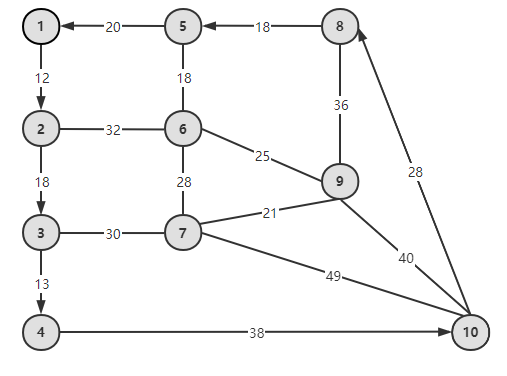
With a graph, we can define a path :
A path is a sequence of arcs or edges connecting two specific nodes in a graph. In this sequence, each arc or edge has exactly one point in common with the arc or edge before it . When passing an arc, you can only pass in the direction marked on the arc. At the same time, no node will be repeatedly traversed by a road .
For example, in the Littleville example, there are many paths from node 3 to node 8, such as 3-7-10-8 and 3-4-10-8, both of which are paths. And 3-7-6-5-8 is not a road, because (5, 8) is an arc, only 8-5; 3-7-6-9-7-10-8 is not a road, because the node is reused 7.
When the arcs and edges in the abstract graph of a practical problem involve cost or length, we face an optimization problem: the shortest path problem is to find the path with the shortest total length between two nodes in the graph.
The Littleville case is a class of shortest path problems with the following basic assumptions:
Figure: Arcs and Edges
cost: non-negative
Output: shortest path
Pairing method: all nodes and other nodes
In addition, the shortest path problem involves two additional categories, which we illustrate with examples.
texas transportation company
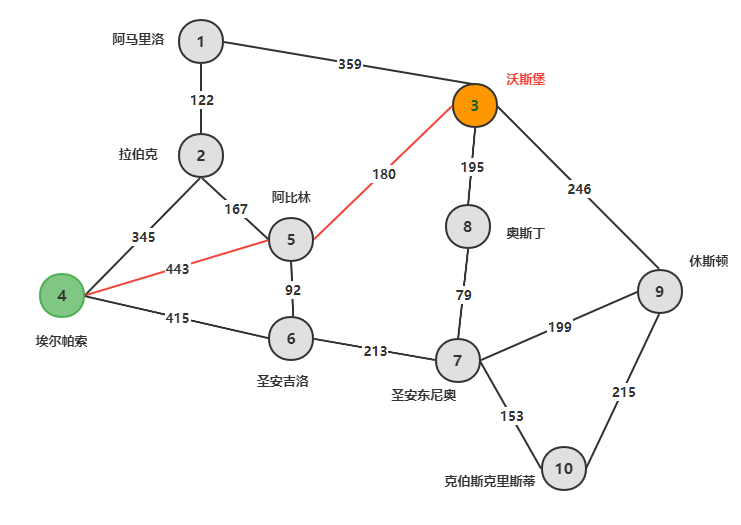
The figure below shows the highway connection map of several important cities in Texas, and the numbers marked on the side represent the standard driving distance (unit: mile).
Texas Transportation Company needs to deliver goods from the central warehouse in Fort Worth to all other cities in the map. The truck departs from the warehouse and goes directly to the destination without loading or unloading the goods in the middle. Drivers can choose their own route from Fort Worth to their destination, but drivers will be paid based on the shortest route from origin to destination. In order to clarify the impact of this proposal on the company, we need to calculate the length of the shortest path from the warehouse to all cities.
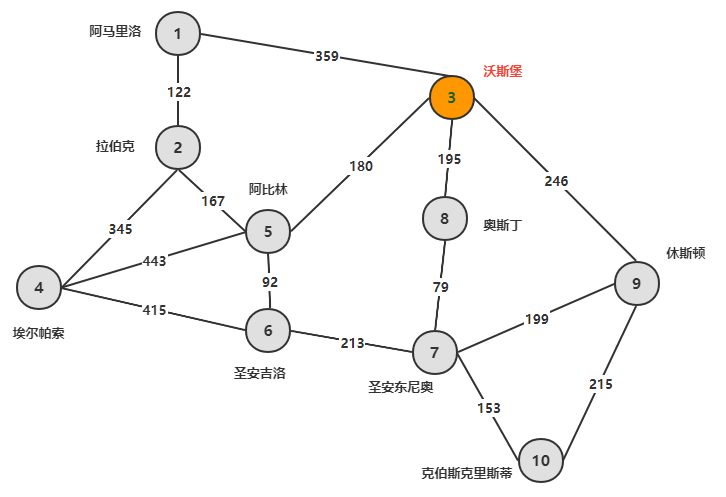
The underlying assumptions of Texas Transit are:
Figure: only edges
cost: non-negative
Output: shortest path
Pairing method: a starting point to other nodes
"Double Ring" Circus
The performance of the "Double Ring" circus is coming to an end. They plan to return to their headquarters in Tallahassee. According to the current arrangement, their last performance will end in Lincoln County, but if the cities on the way back have reservations in advance, it is still possible to perform locally. The image below plots possible return routes and estimated costs in thousands of dollars. The figure also indicates the expected income (unit: thousand dollars) that can be obtained by acting in the city. We hope to find the optimal return route of the circus to maximize the revenue (the revenue here is generated at the node).
This original circus travel network is an undirected graph. Firstly, the income of the nodes must be processed, which must be converted into an equivalent directed graph, and then the income of the nodes is "transferred" to the arc. Since the travel expenses between the two cities are the same, the corresponding directed graph is:
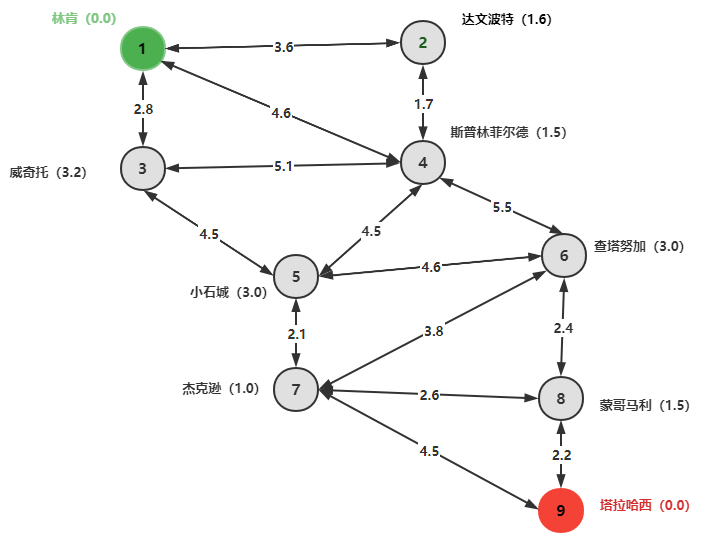
Starting from the cost, transfer the node revenue to the arc: subtract the cost on the arc from the profit of the city at the end of the arc . Merge the "revenue" of the nodes to get the cost from one city to another (the round-trip cost is different at this time):
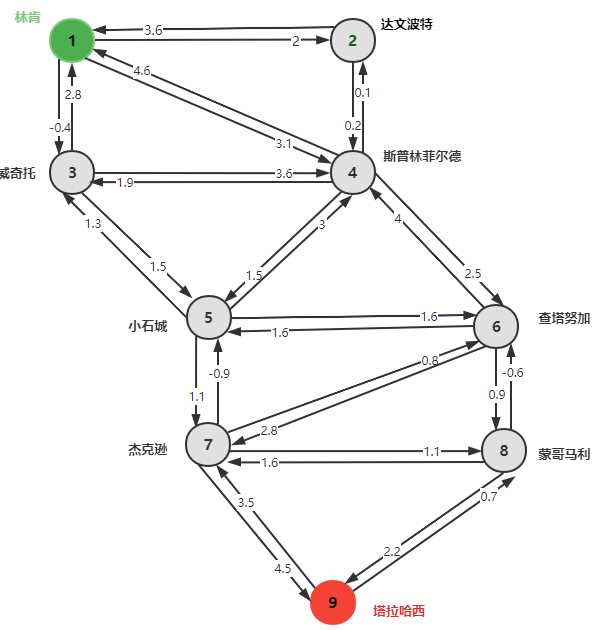
Because the shortest path only allows a node to go through it once, the arc cost calculated in this way is correct. The basic assumptions of the "Double Ring" circus are:
Graph: only arcs (directed graph)
Cost: can be positive or negative
Output: shortest path
Pairing method: one start point to one end point
The above shortest path model can be summarized into two categories: one-to-many and many-to-many shortest path problems.
2
dynamic programming
The method of dynamic programming (dynamic programming) can be used to solve the shortest path problem mentioned above. For this, some mathematical symbols need to be defined:

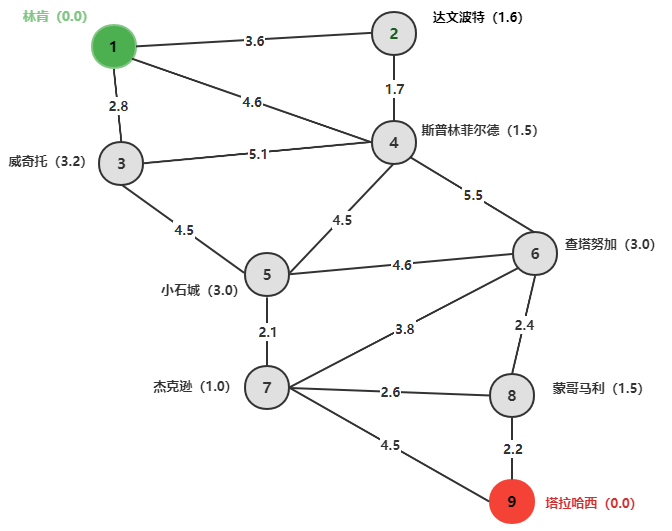
For ease of understanding, give an example. Consider the shortest path problem from starting point 1 to all other nodes in the following graph .
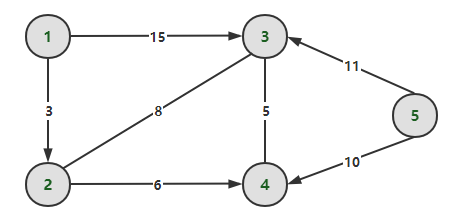
According to the definition, we can get the shortest path length and path of each node:
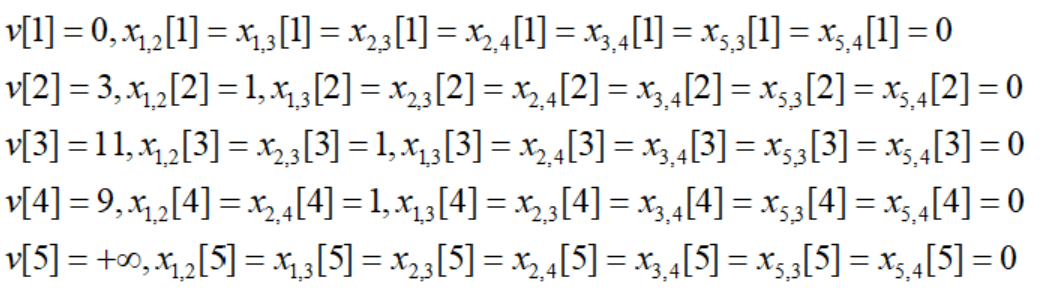
Let's think about this logic below: For the Texas case, the shortest path from 3 to 10 is 3-8-7-10, this road passes through nodes 8 and 7, now consider the shortest path from 3 to 8, it is very Obviously there is only 3-7-8, there is no other shorter road than this one, if there is, you only need to go along this road to 8 first, and then to 10, then there will be a shorter road from 3 to 10 10 way.
Therefore, we have a conclusion: the optimal path must contain the optimal sub path (sub path)
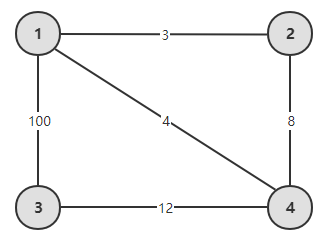
Unfortunately, this conclusion is problematic. Consider the example in the figure below, the shortest path from node 1 to 3 is 1-2-3, but the shortest path from 1 to 2 is 1-3-4-2.

The reason for this phenomenon is that there is a negative dicycle: a cycle refers to a road whose starting point and end point coincide, and a negative weight cycle refers to a cycle whose total length is negative.
The 3-4-2-3 in the above figure is a negative weight cycle with a total length of -10. But fortunately, the negative weight cycle is the only difficult case in the shortest path problem, so the above conclusion is more accurate is defined as: In a graph without negative weight cycles, the optimal path must contain the optimal subpath
With this conclusion, we can use the functional equation of dynamic programming to sort out the recurrence relationship of the shortest path problem. We illustrate this idea with two examples.
Functional equations from one node to other nodes (one-to-many)
In a graph without negative weight cycles, the shortest path function equation from the starting point s to all other nodes is:

Taking Texas transportation as an example, from 3 to 4, after calculation and comparison, we can get:
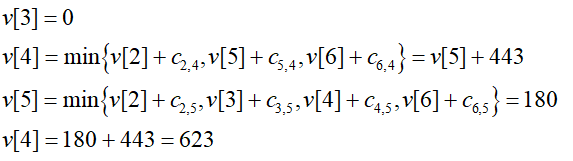
Why does the shortest path of v[4] go through node 5? Because only nodes 2, 5, and 6 are connected to 4, if the shortest subpath passes through node 2, then the distance can only be 122+345 or 167+345, both of which are longer than 443. The same is true for node 6, which can only be 5.
Functional equation from all nodes to all other nodes (many-to-many)
In a graph without negative weight cycles, the functional equation for the shortest path problem from all nodes to other nodes is:

This function equation shows that the shortest path from k to l either contains the arc/edge (k, l), or there is an intermediate point i, and the optimal path contains the shortest path from k to i plus the path from i to l shortest path.
For example, find the shortest path between any two points in the figure below.
Using observation, we get the shortest path from node i to node j and its path:

Then we use the principle to get the shortest path from node 1 to 4 and 2 to 3:
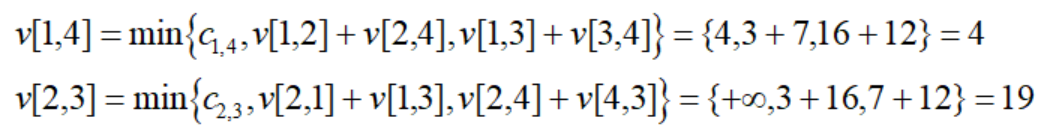
The two examples above demonstrate how dynamic function equations work. But we can also find that the existence of loops will make it impossible to solve the situation of circular dependence caused by functional equations. To do this, we must develop operational algorithms to implement this idea of dynamic programming. These we introduce next time.