Algorithm 15 - Topic in Dynamic Programming

---

1. Recursive and recursive writing of dynamic programming

Dynamic programming: decompose a complex problem into several sub-problems, and obtain the optimal solution of the original problem by synthesizing the optimal solutions of the sub-problems. It should be noted that dynamic programming will record the solution of each sub-problem that has been solved, so that when the same sub-problem is encountered next time, there is no need to repeat calculations.

1. Recursive writing

Take the Fibonacci sequence as an example:

int F(int n){
    if(n == 0 || n == 1)
        return 1;
    else
        return F(n-1)+F(n-2);
}

In fact, this recursive process involves a lot of repeated calculations. Say F(5) = F(4)+F(3), then F(4) = F(3)+F(2). At this time, if no measures are taken, F(3) will be calculated twice. In order to avoid repeated calculations, a one-dimensional array dp can be opened to save the calculated results. And dp[n]=-1 means that F(n) has not been calculated yet:

int F(int n){
    if(n == 0 || n == 1)
        return 1;
    if(dp[n] != -1)
        return dp[n];//已经被计算过
    else {
        dp[n] = F(n-1) + F(n-2);
        return dp[n];
    }
}

A problem is said to have overlapping subproblems if it can be decomposed into multiple subproblems and these subproblems are repeated. Dynamic programming records the solutions of overlapping sub-problems, so that the next time the same sub-problem is encountered, the previously recorded results can be directly used, which in turn avoids a large number of repeated calculations. Therefore, a problem must have overlapping subproblems in order to be solved by dynamic programming.

2. Recursive writing

Take the number tower problem as shown in the figure as an example. From the top floor to the bottom floor, you can only go to one of the connected numbers on the next floor each time. What is the maximum value obtained after adding the numbers on the path at the end?

Use a two-dimensional array f, where f[ i ] [ j ] represents the jth number of the i-th layer, such as f[1][1]=13. First, start from 13 on the first layer, follow the path of 13->11->7 to reach 7, and then enumerate 7 to reach the maximum sum of the bottom layer. After reaching 7 from 13->8->7, also enumerate the maximum sum of 7 to the bottom layer. Therefore, it is advisable to set up a two-dimensional array dp, dp[3][2] represents the maximum sum of 7 reaching the bottom layer

Start solving from the top, then in fact dp[1][1] = f[1][1]+max{dp[2][1],dp[2][2]}

Therefore, the recursive formula can be obtained: dp[i][j] = f[i][j]+max{dp[i+1][j],dp[i+1][j+1]}. And dp[n][j] = f[n][j] is the boundary of recursion. The recursive method always starts from these boundaries, and then continuously calculates the value of each dp upwards, and finally gets the desired answer.

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 1000;
int f[maxn][maxn],dp[maxn][maxn];

int main(){
    int n;
    scanf("%d",&n);
    for(int i = 1 ; i <= n ; i++){
        for(int j = 1 ; j <= i ; j++){
            scanf("%d",&f[i][j]);
        }
    }
    //边界
    for(int j = 1 ; j <= n ; j++)
        dp[n][j] = f[n][j];
    //从第n-1层开始，不断向上计算
    for(int i = n-1 ; i >= 1 ; i--){
        for(int j = 1 ; j <= i ; j++){
            dp[i][j] = f[i][j] + max(dp[i+1][j],dp[i+1][j+1]);
        }
    }
    printf("%d",dp[1][1]);
    return 0;
}

Obviously, it can also be implemented with recursion. The difference is: recursion calculation is bottom-up, while recursion is top-down.

A problem is said to have an optimal substructure if its optimal solution can be efficiently constructed from the optimal solutions of its subproblems. The optimal substructure guarantees that the optimal solution of the metaproblem in dynamic programming can be deduced from the optimal solution of the subproblem. Therefore, a problem must have an optimal substructure to be able to use dynamic programming to solve the problem.

To sum up, a problem must have overlapping subproblems and optimal substructure before it can be solved by dynamic programming.

3. Divide and conquer, greedy and dynamic programming

Divide and conquer and dynamic programming: both decompose the problem into sub-problems, but divide and conquer does not overlap the sub-problems.
Greedy and dynamic programming: Greedy does not require waiting for all sub-problems to be solved before choosing which one to use, but uses a strategy to select a sub-problem to solve, and the unselected sub-problems are discarded.

Second, the largest continuous subsequence and

Topic: Given a sequence of numbers A1, A2,...,An, find i,j such that Ai+...+Aj is the largest, and output the maximum sum

Example: -2 11 -4 13 -5 -2 Obviously 11+(-4)+13=20-bit maximum sum

Ideas:

1. Let the state dp[i] represent the sum of the largest subsequence ending with A[i] (A[i] must be the end of the continuous subsequence)

dp[0]=-2
dp[1]=11
dp[2]=7(11-4)
sp[3]=20(11-4+13)
dp[4]=15(11-4+13-5)
dp[5]=13(11-4+13-5-2)

2. Because dp[i] requires that it must end with A[i], there are two situations:

   (1) The continuous sequence of the maximum sum has only one element: A[i]
   (2) The continuous sequence of the maximum sum has multiple elements, and the maximum sum is dp[i-1]+A[i]
   Therefore, dp[i ]=max{A[i],dp[i-1]+A[i]}

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 10010;
int A[maxn],dp[maxn];
int main(){
    int n;
    scanf("%d",&n);
    for(int i = 0 ; i < n ; i++)
        scanf("%d",&A[i]);
    dp[0] = A[0];
    for(int i = 1 ; i < n ; i++){
        dp[i] = max(A[i],dp[i-1]+A[i]);
    }
    int k = 0;
    for(int i = 1 ; i < n ; i++){
        if(dp[i]>dp[k]){
            k=i;
        }
    }
    printf("%d",dp[k]);
    return 0;
}

3. The longest non-decreasing subsequence (LIS)

Topic: In a sequence of numbers, find the longest subsequence (may not be continuous) such that the subsequence does not descend (non-decreasing)

For example: the existing sequence A={1,2,3,-1,-2,7,9}, the subscript starts from 1, and its longest non-decreasing subsequence is {1,2,3,7,9 }, length 5

Let dp[i] represent the length of the longest non-decreasing subsequence ending with A[i], so there are two cases for A[i]:

1. If the element A[j] before A[i] makes A[j]<=A[i] and dp[j]+1>dp[i], then let A[I] follow A[j] Form a longer subsequence, that is, let dp[i] = dp[j]+1
2. If the element before A[i] is larger than A[i], then A[i] can only form a LIS by itself with a length of 1

For example, there is a sequence A={1,5,-1,3}, the subscript starts from 1, how to get to the longest subsequence ending with A[4]: judge A[1], A[2] in turn , A[3], after judging, A[4] can follow A[1] or A[3] to form a LIS with a length of 2. Another example is the sequence {1,2,3,-1}, where A[4] cannot follow any element, so LIS is -1 element with a length of 1

code:

#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100;
int A[N],dp[N];
int main(){
    int n;
    scanf("%d",&n);
    for(int i = 1 ; i <= n ; i++)
        scanf("%d",&A[i]);
    int ans = -1;//标记最大的子序列长度
    for(int i = 1 ; i <= n ; i++){
        dp[i] = 1;//初始条件是每个元素结尾的最长子序列中只有自己
        for(int j = 1 ; j < i ; j++){
            if(A[i] >= A[j] && dp[j]+1 > dp[i])
                dp[i] = dp[j] + 1;
        }
        ans = max(ans , dp[i]);
    }
    printf("%d",ans);
    return 0;
}

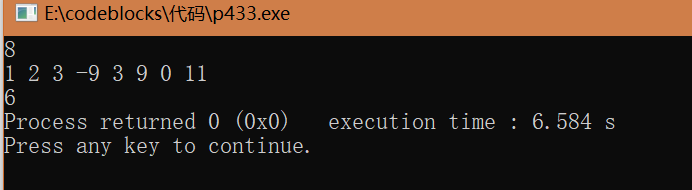
4. Longest Common Subsequence (LCS)

Topic: Given two strings or number sequences A, B, find a string such that this string is the longest common part of A and B (subsequences may not be continuous

For example: the longest common subsequence of the strings "sadstory" and "adminsorry" is "adsory"

Idea: let dp[i][j] represent the LCS length between the i-position of string A and the j-position of string B, and the subscript starts from 1, such as dp[4][5] represents "sads" and the LCS length of "admin", then there may be two situations:

1. If A[i]==B[j], then the length of the common subsequence between string A and string B is increased by one bit, that is, dp[i][j] = dp[i-1][j-1 ]+1, for example, dp[4][6] represents the LCS length of "sads" and "admins", and A[4]==B[6], then dp[4][6]=dp[3] [5]+1, which is 3
2. If A[i]!=B[j], then the LCS between bit i of string A and bit j of string B cannot be extended, then dp[i][j] will inherit dp[i- The larger value between 1][j] and dp[i][j-1]. For example, dp[3][3] is the LCS length of "sad" and "adm", and A[3] is not equal to B[3], then inherit the LCS of "sa" and "adm" or "sad" and "ad" The larger value of the LCS, namely "sad", "ad", is 2

code:

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100;
char A[N],B[N];
int dp[N][N];
int main(){
    int n;
    gets(A+1);//从下标为1开始读
    gets(B+1);
    int lenA = strlen(A+1);
    int lenB = strlen(B+1);
    for(int i = 0 ; i <= lenA ; i++)
        dp[i][0] = 0;
    for(int j = 0 ; j <= lenB ; j++)
        dp[0][j] = 0;
    for(int i = 1 ; i <= lenA ; i++){
        for(int j = 1 ; j <= lenB ; j++){
            if(A[i] == B[j])
                dp[i][j] = dp[i-1][j-1]+1;
            else
                dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
        }
    }
    printf("%d",dp[lenA][lenB]);
    return 0;
}

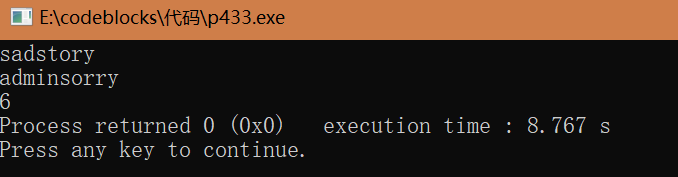
Five, the longest palindrome substring

Topic: Given a string S, find the length of the longest palindrome substring of S
For example: the longest palindrome substring of the string "PATZJUJZTACCBCC" is "ATZJUJZTA" with a length of 9

Idea: let dp[i][j] indicate whether the substring of S[i] set to S[j] is a palindrome substring, and it is 1 if it is, and 0 if it is not. In this way, there will be two situations:

1. If S[i] = S[j], then as long as S[i+1] and S[j-1] are palindrome substrings, then S[i] to S[j] are palindrome strings
2. If S[i]!=S[j], then S[i] to S[j] must not be a palindrome substring

code:

#include<cstdio>
#include<cstring>
const int maxn = 1010;
char S[maxn];
int dp[maxn][maxn];
int main(){
    gets(S);
    int len = strlen(S);
    int ans = 1;
    memset(dp,0,sizeof(dp));
    for(int i = 0 ; i < len ; i++){
        dp[i][i] = 1;
        if(i < len-1){
            if(S[i] == S[i+1]){
                dp[i][i+1] = 1;
                ans = 2;
            }
        }
    }
    for(int L = 3 ; L <= len ; L ++){
        //枚举子串的长度
        for(int i = 0 ; i+L-1 < len ; i++){
            int j = i+L-1;
            if(S[i]==S[j]&&dp[i+1][j-1]==1){
                dp[i][j]=1;
                ans = L;
            }
        }
    }
    printf("%d\n",ans);
    return 0;
}

6. The knapsack problem

1. 0-1 knapsack problem

Title: There are n items, the weight of each item is w[i], and the value is c[i]. There is a knapsack with a capacity of V, how to select items and put them into the knapsack so that the total value of the knapsack is maximized. Only one of each item

Example:

5  8//n=5 V=8
3 5 1 2 2 //w[i]
4 5 2 1 3 //c[i]

Idea: Let dp[i][v] represent the maximum value of the first i items that are just loaded into a knapsack with a capacity of v. For each item:

1. If the i-th item is not placed, then the problem is transformed into the maximum value of the first i-1 items in a knapsack with a capacity of v, that is, dp[i-1][v]
2. Put the i-th item, then the problem is converted to the maximum value that the first i-1 items can be loaded into the knapsack with a capacity of vw[i], that is, dp[i-1][vw[i]]+ c[i]

code:

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100;
const int maxv = 1000;
int w[maxn],c[maxn],dp[maxv];
int main(){
    int n,V;
    scanf("%d%d",&n,&V);
    for(int i = 1; i <= n ; i++)
        scanf("%d",&w[i]);
    for(int i = 1; i <= n ; i++)
        scanf("%d",&c[i]);
    for(int v = 0 ; v <= V ; v++)
        dp[v] = 0;
    for(int i = 1 ; i <= n ; i++){
        for(int v = V ; v >= w[i] ; v--){
            dp[v] = max(dp[v],dp[v-w[i]]+c[i]);
        }
    }
    int max = 0 ;
    for(int v = 0 ; v <= V ; v++){
        if(dp[v]>max){
            max = dp[v];
        }
    }
    printf("%d\n",max);
    return 0;
}

2. Complete knapsack problem

The difference from the 0-1 knapsack problem is that there are infinite pieces of each item

Then for each item:

1. Do not put the i-th item, then dp[i][v] = dp[i-1][v]
2. Put the i-th item, then transfer to dp[i][vw[i]]

即：dp[i][v] = max(dp[i-1][v],dp[i][v-w[i]]+c[i])