1. Step

The optimal solution described problem (optimal solution) structural features
Recursive definition of the optimal solution value
Bottom-up calculated optimum value
Optimum configuration information from the value calculated optimal solution obtained in

2. element

Optimal substructure and overlapping subproblems
optimal substructure character refers to solutions of all the sub-optimal solutions of a problem are included in optimal.
When the dynamic programming recursion avoid double counting the same sub-process problem, the solution for each sub-problem only once, and will save it in a
table, when needed again, look-up table to obtain.

3. The assembly line scheduling

Optimal substructure property: If the optimal solution of the problem is, the solution to all problems is sub-optimal. Here, described as the best
sub-path is the best path.
Prove optimal substructure: pruning method
∵ if the sub-path from the beginning of P1 to S1, j-1 is not optimal, then there must be one to start from S1, j-1 and more preferably the sub-path P2,
to use when P2 after replacing atoms paths P1, will give a better route than the original path, which is assumed to start from S1, j is one of the most
optimal route conflict.
∴ must also be sub-optimal path P1
The fastest time recursive definition optimum route
fastest time f = min (F1 [n-] + X1, F2 [n-] + X2)
to give f value needs to be calculated for each value of fi [j] of
f1 [j] = {F1 min [-J. 1] + A (. 1, J), F2 [-J. 1] + T (2,. 1-J) + A (. 1, J)}
F2 [J] = min {F2 [J- 1] + a (2, j ), f1 [j-1] + t (1, j-1) + a (2, j)}
recursion initial values: f1 [1] = e1 + a (1,1) ; f2 [1] = e2 + a (2,1)
First determine the end of this issue, then the optimal solution from the bottom up value calculation, O (n)
Optimum configuration structure (optimal path output)

4. Matrix Chain

Given a matrix sequence <A1, A2, ..., An >, wherein the dimension of the matrix Ai is Pi-1 × Pi, requires calculation A1 × A2 × ... × An chain matrix multiplication
minimum number of multiplications?

Optimal substructure
dimension of matrixes A_i is P_ (i-1) * P_i , the input sequence is P0, P1 ... Pn, it is
assumed that the solutions to subproblems A_ij (A_i * A_ (i + 1 ) ... A_j) is an optimal solution, then there exists a Aij in the best split point k (i≤k <j),
so that the daughter strand A_ik and a_k + 1, j solution of (A_i * A_ (i + 1 ) ... a_k) and (A_ (k + 1) ... A_j) is optimal.
Optimum value defined recursively
multiplications size of the auxiliary structures n ^ m [i, j] 2 daughter strand storage A_ij = (A_iA_ (i + 1 ) ... A_j) is, m [1, n] denotes the n-th moment all
multiplied by the number of chain matrix multiplication. m [i, j] of the size of the matrix triangular = O (n-^ 2)
I = J When, m [i, j] = 0
I <J when, m [i, j] = min (m [i, K] + m [K +. 1, J] + of P_ (. 1-I) * * PJc P_j ), I <= K <J
Bottom-up value calculated optimum
auxiliary structure s [i, j] for the recording position of the best split point k is
calculated recursively the optimal combination of chain length respectively to 2 n matrix of the chain, a long chain calculation dependent short chain the best results.
Time complexity of O (n ^ 3)

matrix-chain-order(P)
        n=length[p]-1
        for  i=1 to n
          m[i,i]=0
    for l=2 to n            //l为链长
       for i=1 to n-l+1     //具有n-l+1个链长为l的组合
          j=i+l-1
            m[i,j]=∞
            for  k=i to j-1 //找最佳分裂点k
              q=m[i,k]+m[k+1,j]+ P_(i-1)*P_k*P_j
                if q<m[i,j]
                 m[i,j]=q
                   s[i,j]=k //记录最佳分裂点
        return m and s

Output optimal solution structure

The longest common subsequence (Longest Common Subsequece)

So that a given sequence X = {x1, x2, ... xm}, another sequence Z = {z1, z2, ... zk} is a sequence of X must be met: subscript X present in a
strictly increasing sequence i1 <i2 <... <ik, are such that for all j Xij = Zj (1≤j≤k). In other words, the original sequence is the sequence deleted
several elements obtained.
For sequences X and Y, Z sequence of sub-sequence if both X and Y is a sub-sequence, then Z is a common subsequence of X and Y is.

Properties LCS problem optimal substructure
so X = {x1, x2, ... xm}, Y = {y1, y2, ... yn} of two sequences, sequence Z = {z1, z2, ... zk} X and Y a longest common
subsequence, then:

os xm = = xm = a wedyn ZK ZK-1 is 且是 Xm-1 和 In LCS-1 的
if xm ≠ yn, there are two sub-problems, LCS X_m-1 and X and Y and the LCS's Y_m-1.

LCS recursively defined value
so that C [i, j] stored sequence LCS length Xi and Yj, then:

i or j=0时，C[i,j] = 0
i,j>0 and xi=yj时， C[i,j] = C[i-1,j-1]+1
i,j>0 and xi≠yj时， C[i,j] = max{C[i,j-1],C[i-1,j]}

LCS value calculated upwardly from the bottom
O (Mn)
B [I, J] for storing an LCS xi and yi which is the case, the case 1 represents = 0, = 1, and -1 represents X_m-1 and Y, respectively, and an LCS LCS Y_m-1 and X is

def LCS_Length(x,y):
    m=len(x)
    n=len(y)
    for i in range(m):
        c[i][0]=0
    for j in range(n):
        c[0][j]=0
    for i in range(1,m):
        for j in range(1,n):
            if x[i]=y[j]:
                c[i][j] = c[i-1][j-1] + 1
                b[i][j] = 0
                elif c[i-1][j]>=c[i][j-1]:
                    c[i][j]=c[i-1][j]
                    b[i][j] = 1
                else:
                    c[i][j]=c[i][j-1]
                    b[i][j] = -1
        return c,b

The c and b output LCS
improvements:? Directly from x [i] = y [j ], c [i-1] [j], c [i] [j-1] is determined to be banned b [i, j] .

def printLcs(c,x,y,i,j)
  if i == 0 or j == 0:
        return
  if x[i] == y[j]:
      printLcs(c,x,y,i-1,j-1)
      print(x[i])
  elif c[i-1][j]>=c[i][j-1]:
        printLcs(c,x,y,i-1,j)
  else
        printLcs(c,x,y,i,j-1)

6. Optimal binary search tree (Optimal Binary Search Tree)

For single keyword lookup, to find the red-black tree in time O (lgn), but if looking for keywords and each keyword is a series of
different frequency values to find at this time on the whole black tree It can not produce the least time.
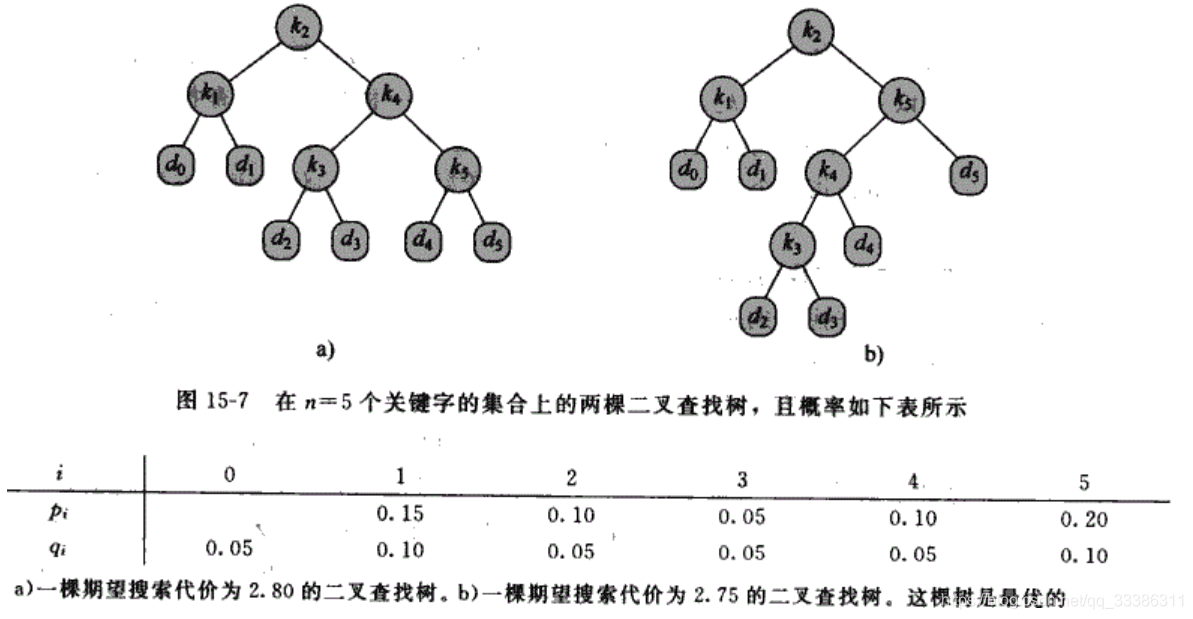
Here Insert Picture Description
So that n different key set K = {k1, k2, ... , kn}, where K1 <K2 <... <KN;
PI: the probability of the search key ki
so d0, d1, ..., dn represents not critical K character set in a virtual (dummy) keyword;
D0: less than all of the key k1; dn: kn greater than all the keywords;
DI: all keywords interposed between ki and ki + 1 (i = 1, 2, ..., the n--1)
qi: the probability of the search key di
keyword search only two states: success Search: find key ki, a probability of pi; unsuccessful Search: find key di, probability qi;
total and the probability (i = 1-> n) pi + pj (i = 0-> n) = 1.
Definition E (searching the costs) = (depth (k_i) +1 ) * p_i (i = 1-> n) + (depth (D_i) + 1'd) * Q_I (I = 0-> n-) =
. 1 + depth (K_i) * P_i (sum i = 1-> n) + depth (d_i) * q_i ( sum i = 0 -> the n-)
E smallest binary search tree is called optimal BST.

Optimal substructure
if Tr is a root with kr and includes ki, ..., ..., kj of OBST, it contains the keyword ki, ... kr-1 left subtree Tl and contain
keywords kr + 1, ..., kj right subtree Tr also OBST. Idea is similar to looking for the best split dot matrix chain.
Recursively defined optimum value
so that e [i, j] containing the keyword ki, ..., kj OBST average cost of retrieval, the e [1, n] of the obtained solution, wherein i≥1, j≤n and j≥ i-1
when j = i-1 when, e [i, j] = q_i-1
when j> = i, e [i , j] = min {e [i, r-1] + e [r + 1, j] + w (i , j)}; wherein
w (i, j) = p_k ( sum k = i-> j) + q_k ( sum k = i-1 -> j );
Calculating the optimal value of solution from the bottom upwards
O (n ^ 3)

Follow me with algorithm - dynamic programming