Customizable constraint systems for succinct arguments study notes (2)

Microsoft Research Center Srinath Setty, a16z crypto research and Georgetown University Justin Thaler, Carnegie Mellon University Riad Wahby 20203 paper " Customizable constraint systems for succinct arguments ".

Preface blogs are:

• Customizable constraint systems for succinct arguments study notes (1)

4. SuperSpartan的Polynomial IOP for CCS

The "SuperSpartan's Polynomial IOP for CCS" discussed in this section is an extension of "Spartan [Set20] polynomial IOP for R1CS". Appendix C shows how to extend SuperSpartan's polynomial IOP to handle CCS+ (that is, CCS with lookup operations).

根据Definition 2.2，假定有某CCS structure-instance tuple with size bounds：
$((m,n,l,t,q,d),(M_0,\cdots ,M_{t-1},S_0,\cdots ,S_{q-1},x))$

For simplicity, let $m,n$ are all powers of 2 (if not, for each matrix$M_i$and witness vector $Z$ is zero-padding, extending$m,n$ is all powers of 2, in the following SNARK protocol, it will not increase the Prover time or Verifier time in SNARK).

The matrix $M_0,\cdots ,M_{t-1}$Parsed as a function: { 0 , 1 } log ⁡ m × { 0 , 1 } log ⁡ n → F \{0,1\}^{\log m}\times \{0,1\}^{\log n }\rightarrow \mathbb{F}{ 0,1}logm×{ 0,1}logn→F. _ Any$\{0,1{\}}^{\log m}\times \{0,1{\}}^{\log The\; input\; of\; n}$ format can be parsed as index$(i,j)\in \{0,1,\cdots ,m-1\}\times \{0,1,\cdots ,n-1\}$ in binary representation. The output of this function is the$(i,j)$ elements.

For Spartan background knowledge, see:

• Blog Spartan: zkSNARKS without trusted setup study notes
• Blog Spartan: zkSNARKS without trusted setup source code analysis
• Vitalik R1CS example SNARK in the blog Spartan proves the basic idea

Extend R1CS in Spartan to CCS representation:

Remark 10:

• O ( qmd log ⁡ 2 d ) O(qmd\log^2d) in Prover runtime in Theorem 1$O(qmd{\log }^{2}Item\; d)$ includes the use of FFT to convert$Multiply\; d$ different polynomials with a degree of 1. FFT is only suitable for certain finite fields.
  Also, the actual CCS/AIR/Plonkish instance, whose$d$ rarely exceeds 100, usually as low as 5 or even 2 [GPR21, BGtRZt23]. Therefore, FFT's$O(d{\log }^{2}d)$ time is much slower than directlyddO ( d 2 ) O(d^2)for multiplying polynomials with$d\; degree\; of\; 1$$O\left(d^2\right)$time. Using Karatsuba algorithm instead of FFT, sub-quadratic-in-$d$ time algorithm, and is suitable for any finite field.

Theorem 1 proves:
For a certain CCS structure and instance, $\mathcal{I}=(M_0,\cdots ,M_{t-1},S_0,\cdots ,S_{q-1},x)$ and the claimed witness$W$。令$Z=(W,1,x)$ .
As mentioned earlier, you can:

• The matrix $M_0,\cdots ,M_{t-1}$Parsed as a function: { 0 , 1 } log ⁡ m × { 0 , 1 } log ⁡ n → F \{0,1\}^{\log m}\times \{0,1\}^{\log n }\rightarrow \mathbb{F}{ 0,1}logm×{ 0,1}logn→F。
• General $Z$ parses as a function:$\{0,1{\}}^{\log n}\to F$。
• Put $(1,x)$ parsed as a function:$\{0,1{\}}^{\log n-1}\to F.$ _ [At this time, it is assumed that$Z$中witness$W$ and$(1,x)$ have the same length$n/2$。】

Function $Z$的MLE$\tilde{Z}$表示为：
$tildeZ(X_0,\cdots ,X_{\log n-1})=(1-X_0)\cdot \tilde{W}(X_1,\cdots ,X_{\log n-1})+X_0\cdot \widetilde{(1,x)}(X_1,\cdots ,X_{\log n-1})(13)$

It can be seen that the right side in equation (13) is a multilinear polynomial. For all ( x 0 , ⋯ , x log ⁡ n − 1 ) ∈ { 0 , 1 } log ⁡ n (x_0,\cdots,x_{\log n -1})\in\{0,1\}^ {\log n}(x0​,⋯,xlogn−1​)∈{ 0,1}logn , it is easy to check with$\tilde{Z}(x_0,\cdots ,x_{\log n-1})=Z((x_0,\cdots ,x_{\log n-1}))$ . (becauseZZThe first half of$Z$$W$ , the second half corresponds to vector$(1,x)$ . )
so the right-hand side in equation (13) isZZThe only multilinear extension of$Z.$

If $(1,x)$ length less than$W$ length (e.g. when converting AIR to CCS according to Lemma 3),$x$ padding with zeros to get$x_{pad}$, so that after padding $(1,x_{pad})$ length andWWSame as$W.$After padding with zeros, Verifier will calculate$\widetilde{(1,x)}(X_1,\cdots ,X_{\log n-1})$ time increase$O(\log n)$ field addition operations. For example, if unfilled$(1,x)$ has length$2^l$ , it is easy to check that has length$n/2$ padding$(1,x_{pad})$的multilinear extension为：
$(X_1,\cdots ,X_{\log n-1})\to (1-X_{l+1})\cdot (1-X_{l+2})\cdots \cdot (1-X_{\log n-1}\widetilde{(1,x)})(X_1,\cdots ,X_l)$

Make the multilinear polynomial for all inputs $(x_1,\cdots ,x_{\log n-1})$ corresponds to the filled$(1,x_{pad})$ , which can be considered as filled$(1,x_{pad})$ unique multilinear polynomials.

Similar to the Spartan paper Theorem 4.1, the "SuperSpartan's Polynomial IOP for CCS" protocol for CCS converted by Spartan R1CS is: the

sum-check protocol can be applied to the polynomial on the right side of equation (14):

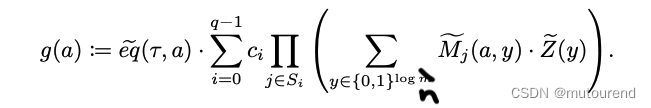
From the Verifier's point of view, this reduces the computation on the right-hand side of equation (14) to "evaluate $g$ at a random input $r_a\in {\mathbb{F}}^m$ ”. And Verifier can itself$O(\log m)$ field operations to calculate$\widetilde{eq}(t,r_a)$ , because it is easy to check:

when Verifier calculates$\widetilde{eq}(t,r_a)$ value, Verifier calculates$g(r_a)$ time is$O(dq)$。对于 i ∈ { 0 , 1 , ⋯   , t − 1 } i\in\{0,1,\cdots,t-1\} i∈{ 0,1,⋯,t−1 } :

For this computation,$t$ sum-check protocol: To this end, introduce random numbers$c\in \mathbb{F}$，并对${\tilde{M}}_i(r_a,y)\cdot \tilde{Z}\left(y\right)$do random linear combination, the weights are$[c^0,\cdots ,c^{t-1}]$。

In the sum-check protocol, Verifier only needs to check the above $t$ polynomials${\tilde{M}}_i(r_a,y)\cdot \tilde{Z}(y)$ evaluate at $r_y$，即意味着Verifier evaluate ${\tilde{M}}_i(r_a,r_y)$ is sufficient. Such a premise assumes that Verifier has query access to${\tilde{M}}_0,\cdots ,{\tilde{M}}_{t-1}$, according to equation (13), Verifier only needs to $\tilde{W}$ and$\widetilde{(1,x)}$Each query can get $\tilde{Z}(r_y)$。

The pseudocode of the "SuperSpartan's Polynomial IOP for CCS" protocol implemented in this paper is as follows:

In short, the "SuperSpartan's Polynomial IOP for CCS" protocol implemented in this paper has the following properties:

According to the above "SuperSpartan's Polynomial IOP for CCS" protocol pseudocode, it includes two sum-check protocol calls:

• 1) When the sum-check protocol is triggered for the first time in step 3.a, the main workload of Prover is:
  
  
• 2) Call the sum-check protocol for the second time in step 3.c, corresponding to $\log Polynomial\; of\; n$ variables:
  
  the degree of each variable is at most 2. Using the standard linear-time-sum-check technology [CTY12, Tha13] in the sum-check protocol, the time used by Prover is$O(N+t)$。

5. Avoid preprocessing in uniform IR

When there is a "uniform" structure in the CCS instance (for example, a circuit has multiple identical sub-circuits), in order to achieve succinct verification cost, the preprocessing of the circuit structure should be avoided.
For the uniform CCS instance, this article implements:

• Verifier可evaluate the multilinear extension polynomials ${\tilde{M}}_0,\cdots ,{\tilde{M}}_{t-1}$ at any desired point in time logarithmic in the number of rows and columns of these matrices。

5.1 Multilinear extension of "adding 1 in binary" function

Integer { 0 , 1 , ⋯ , D − 1 } \{0,1,\cdots, D-1\} can be{ 0,1,⋯,D−1 } in binary representation. Integer$D-An\; index\; of\; 1$ can be represented by a vector of all ones, and an index of integer 0 can be represented by a vector of all zeros. In this index notation, the rightmost bit can be thought of as a low-order bit.

For a bit-vector i ∈ { 0 , 1 } log ⁡ D i\in\{0,1\}^{\log D}i∈{ 0,1}logD，令$\text{to-int}(i)={\sum }_{j=0}^{\log D-1}{i}_j\cdot 2^j$ corresponds toiiThe integer represented by$i\; .$For integer$K\in \{0,1,\cdots ,t-1\}$，$\text{bin}\left(k\right)$ display$\kappa$ corresponds to the binary representation.

Define the function:
next ( i , j ) : { 0 , 1 } log ⁡ D × { 0 , 1 } log ⁡ D → { 0 , 1 } \text{next}(i,j):\{0,1\ }^{\log D}\times \{0,1\}^{\log D}\rightarrow \{0,1\}next(i,j):{ 0,1}logD×{ 0,1}logD→{ 0,1 }
where:

• $i,j$ is bit-vector input
• This and this integer $I=\text{to-int}(i)$和整数$J=\text{to-int}(j)$满足$J=I+1$ , the function output is 1, otherwise it is 0.

The function can therefore be called the "adding 1 in binary" function:

• The input is 2 bit-vectors, and it is judged whether the second input integer is the first input integer plus 1.

Notice:

• young $i$ is all 1 vector, then for allj ∈ { 0 , 1 } log ⁡ D j\in\{0,1\}^{\log D}j∈{ 0,1}logD , all have$(i,j)=0$。

Thus there is Theorem 2:

the actual analysis is divided into 3 situations:

the next is to explain the equation (16) can be evaluated at any point $(r_x,r_y)\in {\mathbb{F}}^{\log D}\times F^{\log D}$ in $O(\log D)$ time：

• It is easy to see that $h(r_x,r_y)$可evaluate in $O(\log D)$ time。
• ggEach summation item in$g$$(r_x,r_y)$ in $O\left(\log D\right)$ time。
• ggThere are O ( log ⁡ D ) O(\log D)in$g$$O\left(\log D\right)$ summation terms, so the total time bound is$O(\log D^2)$。
• However, if adjacent terms of the sum have nearly identical factors, this runtime can be reduced to $O\left(\log m\right)$ . For example, if$v\left(k\right)$ is the kkthin the summation$k$ items, then:
  
  

5.2 CCS converted from AIR

In this section, $m$表示AIR的参数，有$w_{AIR}\in {\mathbb{F}}^{(m-1)\cdot t/2}，z_{AIR}\in F^{(m+1)\cdot t/2}$ . At the same time$m$ represents the CCS matrix$M_0,\cdots ,M_{t-1}$the number of rows. This section also assumes that $m-1$ is a power of 2, and for$M_0,\cdots ,M_{t-1}$Fill with zeros so that the number of rows is a power of 2 (this padding will not increase the Verifier or Prover time in SuperSpartan). That means the filled $M_0,\cdots ,M_{t-1}$The number of rows is no longer $m$ , but$2(m-1)$ .
This processing is convenient for implementation based on the actual domain, and with the help of the multilinear extension of the "adding 1 in binary" function in the previous section, the actual expression of CCS converted from AIR is further optimized.

5.3 Avoiding preprocessing in SIMD CCS

6. Compile Polynomial IOP for CCS to SNARK for CCS