The concept of a graph: the data structure of a graph consists of two sets, one is the vertex set V (vertex), and the other is the edge set E (Edge); undirected graphs are generally recorded as G(V , E); directed graphs are recorded as G<V, E>
A directed graph means that the direction of the edge is distinguished by direction, for example, from A->B; from A to B, but B cannot reach A (the edge of the directed graph is an arrow, called an arc, and the arc head is w , the arc tail is v)
The edges of an undirected graph have no direction distinction, as long as AB, you can go from A to B, and from B to A
The important concepts are as follows:
1: The graph must not be an empty graph, that is to say, the vertex set must not be empty, and the edge set can be empty
2: Complete graph: If there is an edge between any two vertices (note that the edge here is any two vertices directly connected to each other), then the graph is said to be complete.
An undirected complete graph has n*(n-1) / 2 edges.
A directed complete graph has n*(n-1) edges
3: Subgraph: A new graph composed of a certain part of the vertices in the graph and a part of the edges connected to the vertices is the subgraph. (Note that it must not simply say "a subset of edges" and "a subset of vertices", it must be the edges connected to the vertices to form a subgraph)
For undirected graphs, super important concepts are:
4: Connected: If there is a path from vertex A to vertex B, then AB is said to be connected
5: Connected graph and non-connected graph: If any two vertices in the graph have paths (not necessarily directly connected paths, Note here that it is distinguished from the concept of a complete graph), the graph is called a connected graph, which literally means "the whole graph is connected", if some vertices are not connected to other vertices, that is, some vertices are isolated , it is called a disconnected graph.
6: Connected component (also called maximally connected subgraph): If there is ABC connected and DE connected in a graph G, it is said to have two connected components, that is, two maximally connected subgraphs (that is, in graph G, , a connected subgraph).
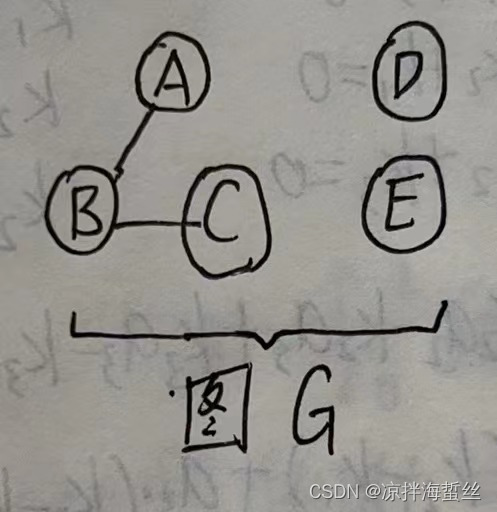
(7) For an undirected graph, N vertices need at least N-1 edges to form a connected graph (drawing is easy to understand), if N vertices need to form a complete graph, at least n*(n-1) is required /2 sides.
If the number of edges is less than n-1, the graph must be disconnected.
For directed graphs, the super important concepts are:
8: Strong connectivity: This concept must be distinguished from the connectivity of undirected graphs, because directed graphs are directed, so its connectivity must be "stronger" connectivity, so remember strong connectivity. If AB is strongly connected, there must be A->B and A<- B; that is, both directions must exist to be called strong connectivity.
9: Strongly connected graph: If in the directed graph G, any two vertices in the graph have a path (no direct connection path is required, N vertices can pass through, as long as there is a path), then the graph G is a strongly connected graph
10: Strongly connected component (also called extremely strongly connected subgraph): It must be distinguished from the concept of connected component in an undirected graph. Strongly connected component means that there must be a cycle in the subgraph, so it is judged whether there is a strong connected component in a directed graph. For connected components, we must find a loop. If there is no loop, it proves that the last vertex D cannot be traced back to the first vertex A, that is, there is no path from D to A, then it is not strongly connected.
11: For a directed graph, a directed graph with N vertices requires at least n edges (forming a ring) to form a strongly connected graph. To form a directed complete graph (a directed complete graph must be a strongly connected graph, and any vertex has two back and forth arrow paths), n*(n-1) edges are required.
Maximally connected subgraphs and minimally connected subgraphs:
12: They are all for undirected graphs. The difference between maximum and minimum is that the maximum must contain all the edges of the subgraph, that is to say, not only must it be connected, but also retain all the edges. Minimal connected subgraphs only need to keep the minimum number of edges to ensure that the graph is connected, that is to say, it can be connected.
Note ⚠️: The spanning tree is a minimally connected subgraph, but the spanning tree is not a maximally connected subgraph (because it does not contain all edges), so of course the spanning tree is not a connected component
Dense and sparse graphs:
13: Denseness and sparseness are for edges. The number of edges is dense, and the number of edges is sparse. (Imagine it as a fishing net. If there are many sides, the whole net will be very dense; if there are few sides, the whole net will be very sparse)
Examples of graphs:
(1) An undirected graph with N vertices and N edges must have a cycle (it can be found by drawing the graph that if each vertex has an edge, there must be a cycle); but note that a cycle is not necessarily connected. It depends on the number of edges (if an undirected graph with n nodes has n*(n-1)/2 edges, it must be a complete graph, and the complete graph must be connected and have a cycle) and from a certain vertex Whether to perform deep search or wide search can traverse the entire graph.
(2) The traversal of the graph is not simply starting from a certain vertex and traversing the rest of the vertices. Because the graph may be disconnected, starting from a certain vertex, only a certain subgraph can be traversed, and the vertices in the other subgraphs cannot be traversed, so to traverse the graph, the vertex set V must be looped through, and the traversed vertices are marked with If there are still some vertices that have not been marked with traversal marks after one traversal is completed, the next cycle will start until all the vertices of vertex set V are marked with traversal marks (the vertices in the subgraph at this time have also been marked traversal) is considered a complete graph traversal.
(3) A non-connected undirected graph with 28 edges has at least () vertices
Analysis: There are 28 edges that are not connected, and the minimum number of vertices is required. If the number of vertices is the fewest, and the number of edges is consumed, then it must be complete For this prodigal son, let’s see how many undirected complete graphs can be formed by 28 edges, and substitute the formula: N*(N-1) / 2 = 28; the solution is N = 8; 8 vertices are formed by 28 edges A completely undirected graph is created, but the topic is not connected, then add an isolated vertex, 9 vertices are enough. There are many similar topics, but they are all about the formula of the number of edges of the complete graph of the undirected and directed graph.
(4) [2010] If there are 7 vertices in the undirected graph G(V , E), to ensure that the graph G is connected in any case, at least (16) edges are needed because it has 7 vertices,
and To ensure that any situation is connected, you can only see how many edges it adds, and adding another edge must be connected, that is, first let its 6 vertices form an undirected complete graph, consuming 6 * (6-1) / 2 = 15 edges, then + 1 = 16, so it must be connected to the seventh vertex. In this way, the graph G must be guaranteed to be a connected graph. Because 15 edges have already filled 6 vertices, they have no place to add another edge, and they can only have a relationship with the seventh vertex. Once a relationship occurs, a connected graph will be formed immediately.
For an undirected graph with 6 vertices , when there are () edges, it can be guaranteed to be a connected graph *(5-1)/2 = 10 edges, at this time +1 edge = 11, it will definitely have a relationship with the sixth vertex to form a connected graph
(5) The graph G has n vertices. If it is a connected undirected graph, the number of edges is at least:
According to the formula, as long as the connectivity is guaranteed, an undirected graph with n vertices only needs n-1 edges.
If it is a strongly connected directed graph , the number of edges is at least:
According to the formula, to ensure strong connectivity, n vertices must use n edges to surround a ring
(6) The undirected graph G has 23 edges, 5 vertices with degree 4, 4 vertices with degree 3, and the rest are vertices with degree 2. How many vertices does graph G have in total?
Analysis:
One edge can contribute two degrees, so there are 46 degrees in total, and 5 vertices with degree 4 consume 20 degrees; 4 vertices with degree 3 consume 12 degrees; the remaining 46 - 12- 20 = 14; the title says that the rest are of degree 2, then 14 / 2 = 7; that is, there are 7 vertices of degree 2, and graph G has a total of 7 + 5 + 4 = 16 vertices
(7) If an undirected graph with n vertices and e edges is a forest, then the forest must have () trees
. An extreme but reasonable example (for example, a tree with a degree of 3, has 10086 nodes, ask the depth and height of the tree, directly use 10083 as the number of node stacks, and the last 3 as the perverted example of leaf nodes) Idea
1 : Here we assume that there are x trees in the forest, then I need to use x-1 edges to form a new tree, but there are e edges in the original x trees, so the new tree has a total of There are x-1+e edges. According to the nature of the tree, except the root node has no edge connected to it, every other node has at least one edge pointing to it, so the number of summary points = total number of edges + 1
is n = (x-1+e) + 1
x = ne
Idea 2: For example, if I assume that each of e edges is connected to two vertices to form a tree, then 2e vertices are consumed to form an e tree, and the remaining vertices form a single tree without The edge tree, that is, the remaining: n - 2e vertices, a total of n - 2e trees;
then there are a total of: n-2e+e = n - e trees
(8) [2017] Known undirected graph G contains 16 edges, 3 vertices with degree 4, 4 vertices with degree 3, and other vertices with degree less than 3, then the vertices contained in graph G The number is at least ()
analysis:
16 sides dedicate 32 degrees, degree 4 has 3, consumes 12 degrees; degree 3 has 4, consumes 12 degrees; then the remaining: 32 - 12 -12 = 8 degrees;
remaining There may be vertices with a degree of 1 and 2, but the number of vertices included in the topic must be at least, that is, the minimum number of vertices allowed, then I must choose a degree of 2, such a vertex consumes 2 degrees, and can consume the remaining as soon as possible degrees. 8 / 2 = 4; that is, only 4 more vertices with a degree of 2 are needed.
Then there are total vertices:
3 + 4 + 4 = 11
graph storage
Adjacency matrix method (suitable for dense graphs):
typedef struct {
char v[100];
int e[100][100];
} Graph;
When the adjacency matrix method stores an undirected graph, it must be a symmetric matrix, because it does not distinguish between in-degree and in-degree. Since it is a symmetric matrix, it supports compressed storage, that is, only the upper or lower triangular part is stored, so in dense In the application of graph, it has very good effect.
Its specific storage method is as follows:
For an undirected graph with 4 vertices
(1) assuming that there are ABCD vertices, a 4*4 square matrix is generated, and the rows and columns are ABCD, and then sequentially from the first row to the first A column starts with 01 (with side 1, without side 0).
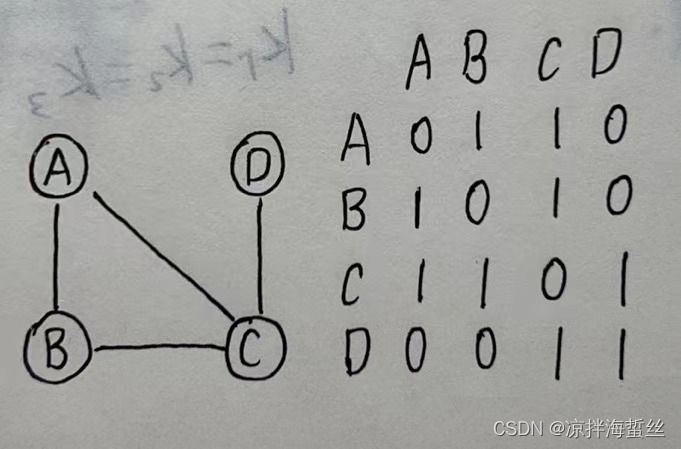
Since the number of this matrix is 1, it represents how many routes there are from a certain point to a certain point with a path length of 1. Then it can be clearly seen that from A to The length of A is zero, A to B, and B to C.
(2) If the matrix is multiplied by itself, the square of the matrix is obtained. The square degree is 2, which means from a certain point to At a certain point, how many routes are there with a path length of 2:

For example, reflected from the matrix, there are 2 routes from A to A with a path length of 2, which are [A] and [B] (the first row of the left matrix Two columns) multiplied by 【B】【A】(the first row of the second column of the matrix on the right) +【A】【C】 multiplied by 【C】【A】 = 2. It also means that these two routes are: from A to B, and then from B to A; or from A to C, and then from C to A; is it
amazing, give another example: the new matrix from C to There are 3 routes with a path length of 2 in C, which are:
【C】【A】multiplied by 【A】【C】 + 【C】【B】multiplied by 【B】【C】 + 【C】【D 】Multiplied by 【D】【C】 = 3
That is to say, from C to A and then from A back to C,
from C to B and then from B back to C,
from C to D and then from D back to C
perfectly combine the route and route The numbers are displayed.
(3) If the square is multiplied by itself to form a cubic matrix, it represents how many routes there are from a certain point to a certain point with a path length of 3, and how to go, it will be clear:
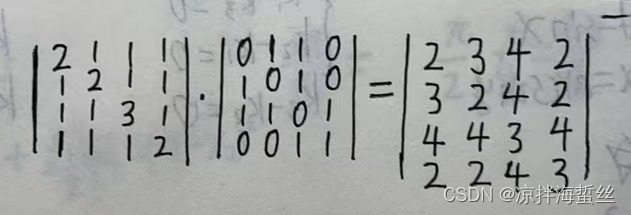
Based on the path length of 2, there are 4 routes from A to C with a path length of 3, which are:
(1) 【A】【A】multiplied by 【A】【C】 + (2) 【A】【B】multiplied by 【B】【C】 + (3) 【A】【D】multiplied by 【D】 [C] = 4
The matrix on the left is obtained on the basis of squares, so we need to look at the roadmap when we return to squares:
it represents 4 paths with a length of 3:
(1)
where [A] [A] is a matrix The path generated when squaring【A】【B】multiplied by 【B】【A】+【A】【C】multiplied by 【C】【A】 = 2 from A to B, then from B back to A, and then
from From A to C
, from A to C, then from C back to A, and then from A to C
(2)
[A] [B] is the path generated when the matrix is squared [A] [C] multiplied by [C] [ B] = 1
from A to C, then from C to B, and then from B to C
(3)
[A] [D] is the path generated when the matrix is squared [A] [C] multiplied by [C] [D] = 1
from A to C, then from C to D, and finally from D back to C
Although it seems silly to go around like this, it can indeed indicate to us that a road leads from a certain point to a certain point. If you don't want to go back, you can add other business logic to filter it out. This effect is still very powerful.
An adjacency matrix stores a directed graph:
The directed graph uses 1 to represent the outgoing degree, which means that the corresponding subscript of the outgoing graph is 1, and the incoming degree is 0 (it is easy to understand, because here 1 means that this road is passable, and the incoming degree of the directed graph is for the current vertex It is impassable, which is equivalent to no road, so it is 0, only the out degree is passable, which is 1)
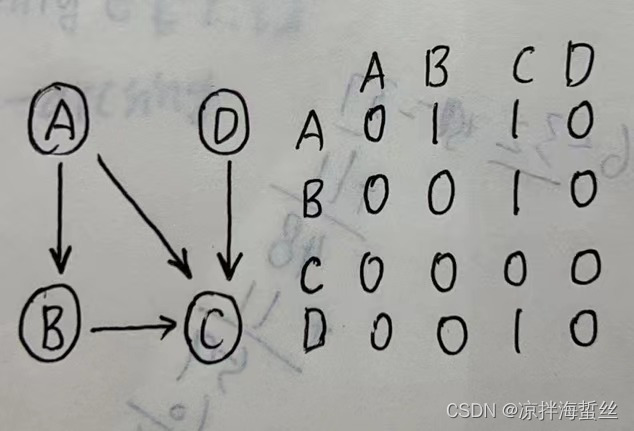
here also refers to the path length of 1, if you want to see the path length of 2, you can also do this The square of the matrix is the same as the undirected graph
Advantages:
Intuitive, convenient and simple, easy to implement coding.
If it is to store a dense graph, if it is an undirected graph combined with the compression method of converting the upper and lower triangular matrix to a one-dimensional array, it can save a lot of space.
Disadvantages:
The efficiency is relatively low, the amount of calculation is large, and the storage of intermediate results will take up a lot of memory space.
Since the matrix is fixed to be an n*n square matrix, if it is a sparse graph, a lot of unnecessary empty storage space will be generated.
If you want to delete a node in the adjacency matrix, you need to traverse, time complexity O(n)
adjacency list method
In order to store sparse matrices more efficiently and conveniently, there is an adjacency list method, which uses the storage method of array + linked list (similar to a hash table), assigns an array subscript position to each vertex, and at the same time assigns the position of the array subscript connected to the vertex The array subscripts of the vertices are linked behind the nodes.
// 边表结点
typedef struct ArcNode{
int index; // 该边指向的顶点的数组下标
struct ArcNode *next; //下一个边表结点的指针
} ArcNode;
// 顶点表结点
typedef struct VNode{
char data; // 顶点信息,存储例如:ABCD,1234之类的值
ArcNode *next; // 链接第一个边表结点
} AdjList[100];
// 邻接表结构
typedef struct {
AdjList[100];
int vexnum; arcnum; // 顶点数和弧数
} ALGraph
If it is an undirected graph, an edge will exist in two edge table nodes at the same time; if it is for a directed graph, only the edge will be recorded, and an edge will only exist in one edge table node (this figure is taken from Wangdao
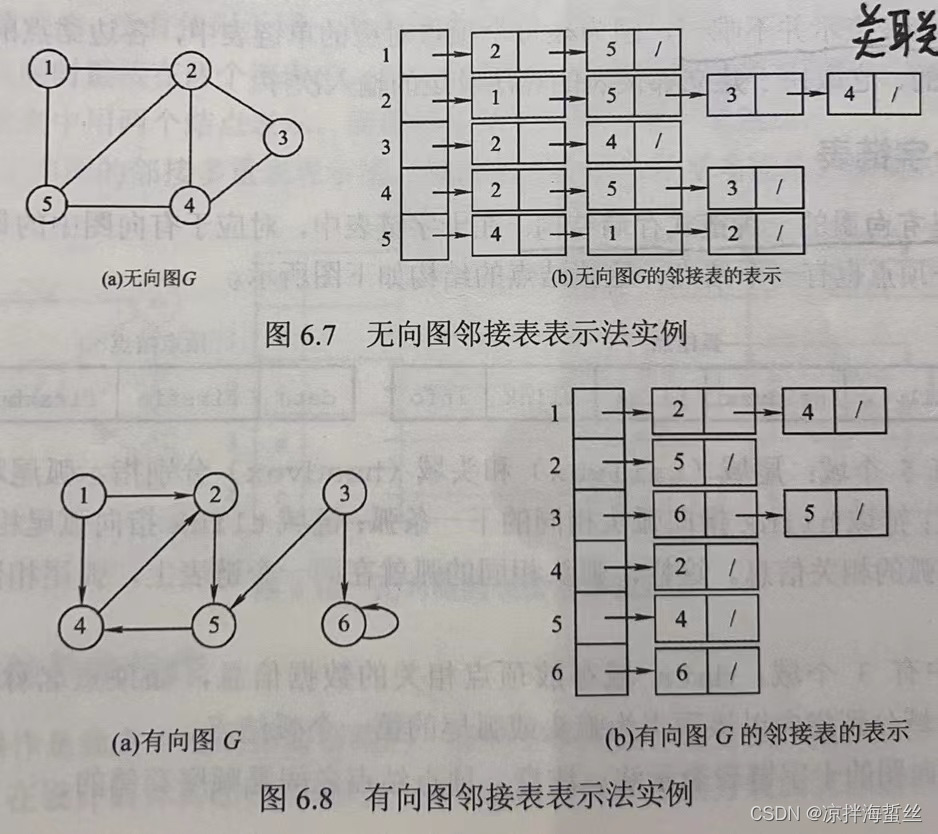
Data structure)
If the adjacency list is used to store the undirected graph, then there must be an even number of edge table nodes; if it is an odd number of edge table nodes, then it must be a directed graph.
Example:
(1) The adjacency list of an undirected graph with n vertices has at most (n*(n-1)) edge list nodes Analysis
: For an undirected graph with n vertices, if it is a complete graph, it has the most edges, There are at most n*(n-1) / 2 edges, and each edge will generate two edge table nodes, so there will be at most n*(n-1) edge table nodes.
(2) Assuming that there are n vertices and the directed graph of e edges is represented by an adjacency list, the time complexity of deleting all edges related to a certain vertex v is: O(n+e) Analysis: To delete
a
certain For all the edges of the vertex, it is necessary to loop through to find the corresponding vertex v, and then delete its outgoing edge table in turn. At this time, all the outgoing edges of the vertex v are deleted, because there are at most n-1 outgoing edge tables, that is, assuming v has outgoing edges for all other vertices
. In the above cycle, its incoming edges must be deleted. To delete incoming edges, first traverse the vertex table nodes O(n), and find the outgoing edge tables of the vertex table nodes except V one by one. Link O(e), delete the outgoing edge related to V, so that the incoming edge of V will also disappear, the
total complexity is O(n+e)
(3) [2021] It is known that an undirected connected graph G is composed of a vertex set V and an edge set E, |E|>0, when the number of vertices with an odd degree in G is an even number not greater than 2, G contains All paths with a length of |E| (called EL) paths (graph G is stored in an adjacency matrix)
(1) Design an algorithm to judge whether there is an EL path in G, if it exists, return 1, otherwise return 0; give the algorithm The basic idea
(to tell you the truth, at that time, I saw what the title described at the time. The number of vertices with an odd degree and an even number not greater than 2 included the EL path. This section has been stuck for a long time and I didn’t want to understand it. It is also after reading the analysis that we know that we only need to count the number of vertices with an odd number, and see if it is 0 or 2, regardless of the feather EL path) Since I use the adjacency matrix, I only need to start the outer loop
from Traversing from the first line to the last line, the memory loop traverses from the first column to the last column, each line is the in-out degree information of a vertex, if it is 1, then ++, and finally use its degree to judge whether %2=0, if yes, Prove that the current vertex is even, if not, prove that the degree of the current vertex is odd, odd vertex sum++;
finally check whether the sum is 0 or 2, if yes, there is an EL path, if not, there is no.
(2) Code
(3) Explain the time complexity and space complexity of the designed algorithm
Since the adjacency matrix is a square matrix of n*n, the cycle cost is O(n^2); the space complexity is O(1)
Graph traversal:
Depth-first BFS (concentrate on one path to the end, when there is no way to go, and then go back and choose another path)
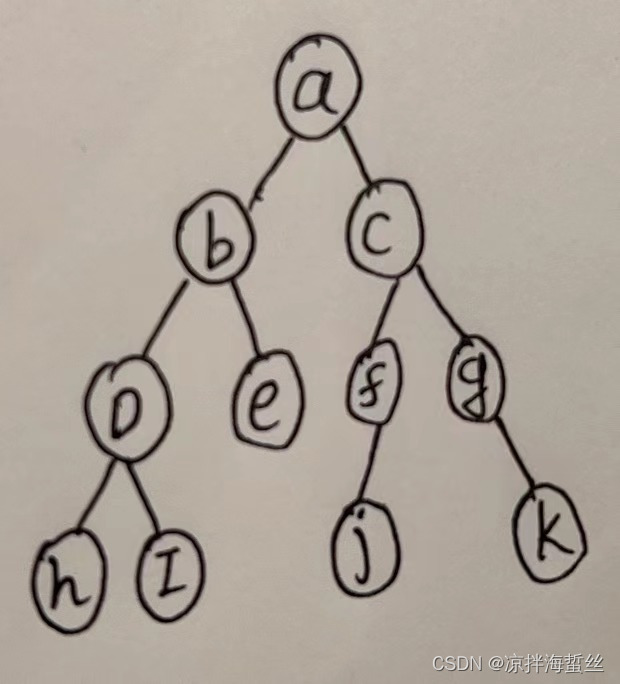
Process:
Initialize an auxiliary queue
(1) Assuming that starting from the root node a, there are b and c nodes connected, then first put a into the queue, then put a out of the queue, and then put b, c into the queue (2) b
out Team, put de near b into the team; c out of the team, put fg near c into the team
(3) d out, hi in, e out, nothing in the team, f out, j in, g Out of the team, k into the team
(4) hi out of the team, jk out of the team
(5) depth search is completed
Due to the use of an auxiliary array, the size is generally set to the number of vertices, and the space complexity is O(V)
when using the adjacency list storage Time: When
searching for the connection point of the vertex, it is groping along the edge, so each edge must traverse one side, and the time complexity is O(E).
When using adjacency matrix storage:
due to the square matrix of N*N vertices , the time complexity is O(V^2) times
A tree can be generated according to breadth first, called breadth first spanning tree, but breadth first spanning tree is not unique
Breadth-first DFS (from near to far, each step in each direction)
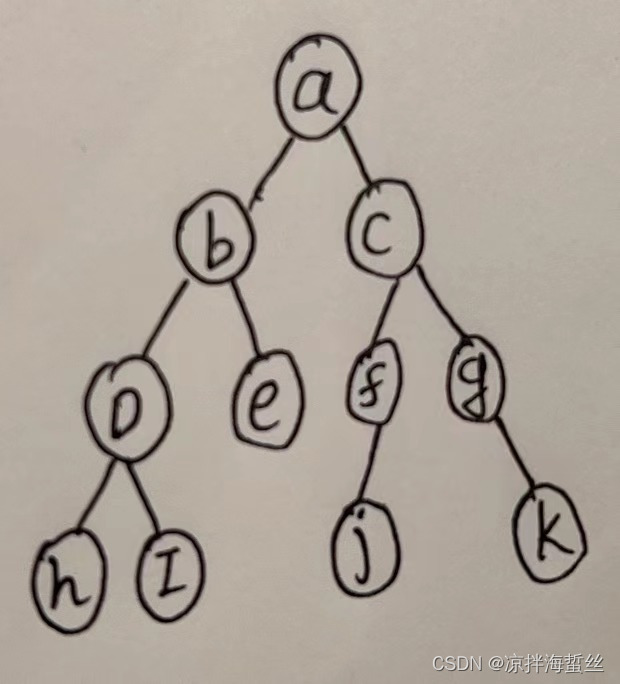
Depth search is generally carried out recursively
(1) start from a, first find b, b to d, d to h, the first path comes to an end, return to d
(2) d to i, the second path also ends Yes, return to d, d finds that this road has been passed, returns to b
(3) b to e, at the end, returns to b, b finds that the road has been passed, returns to a
(4) a to c. . . . . .
(5) Continue steps 1 to 4 until all the paths are gone. This is the depth-first search
How many vertices there are, how many times will it recurse, and the recursive work stack used for recursion, so the space complexity is O(V)
When using adjacency list storage:
the time complexity is O(V + E);
when using adjacency matrix storage:
due to the square matrix of N*N vertices, the time complexity is O(V^2) times