Article Directory
0 Notes
Derived from [Machine Learning] [Whiteboard Derivation Series] [Collection 1~23] , I will derive on paper with the master of UP when I study. The content of the blog is a secondary written arrangement of notes. According to my own learning needs, I may The necessary content will be added.
Note: This note is mainly for the convenience of future review and study, and it is indeed that I personally type one word and one formula by myself. If I encounter a complex formula, because I have not learned LaTeX, I will upload a handwritten picture instead (the phone camera may not take the picture Clear, but I will try my best to make the content completely visible), so I will mark the blog as [original], if you think it’s not appropriate, you can send me a private message, I will judge whether to set the blog to be visible only to you or something else based on your reply. Thank you!
This blog is the notes of (Series 8), and the corresponding videos are: [(Series 8) Exponential Family Distribution 1-Background], [(Series 8) Exponential Family Distribution 2-Background Continued], [(Series 8) Exponential Family Distribution 3- The exponential family form of Gaussian distribution], [(series 8) exponential family distribution 4-log partition function and sufficient statistics], [(series 8) exponential family distribution 5-maximum likelihood estimation and sufficient statistics] , [(Series 8) Exponential Family Distribution 6-Maximum Entropy Angle (1)], [(Series 8) Exponential Family Distribution 7-Maximum Entropy Angle (2)].
The text starts below.
1 background
For a given statistical problem, the statistic that contains all the useful information about the problem in the original sample is called a sufficient statistic. For the estimation of unknown parameters, the statistic that retains all the information about the unknown parameter θ in the original sample is a sufficient statistic.
1.1 The general form of the exponential family distribution
The exponential family distribution is such a type of distribution in the form: in the
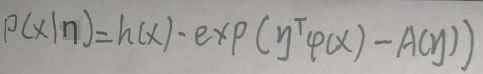
above figure, x belongs to R p , h(x) is a function of x, and sometimes it can be set to 1 (in the exponential family of [2 Gaussian distribution] The form will be mentioned in the section), the type of η is a vector, η is related to the parameter θ of the specific problem, φ(x) is called a sufficient statistic, and A(η) is called a logarithmic partition function. The following figure explains why A(η) is called the logarithmic partition function: the

exponential family distribution includes: Gaussian distribution, category distribution, polynomial distribution, Poisson distribution, beta distribution, Dirichlet distribution, gamma distribution, etc., all of which belong to the exponential family distribution.
1.2 Conjugate prior
For the formula:
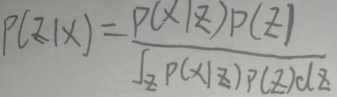
P(z) is the prior probability, that is, the probability of obtaining z through experience or analysis before the training data x. P(x|z) is the likelihood function. P(z|x) is the posterior probability, which is a conditional probability, that is, the probability of z occurring when there is training data x.
The conjugate prior refers to: if the prior probability distribution and the posterior probability distribution have the same form , then the prior distribution and the likelihood function are said to be conjugate. The result of conjugation is that the prior and the posterior have the same form , but the parameters are different.
2 The exponential family form of the Gaussian distribution
This section focuses on the one-dimensional Gaussian distribution. First set the parameters θ=(μ,σ 2 ), the following figure changes the density function of the one-dimensional Gaussian distribution to the form of the exponential family distribution formula:
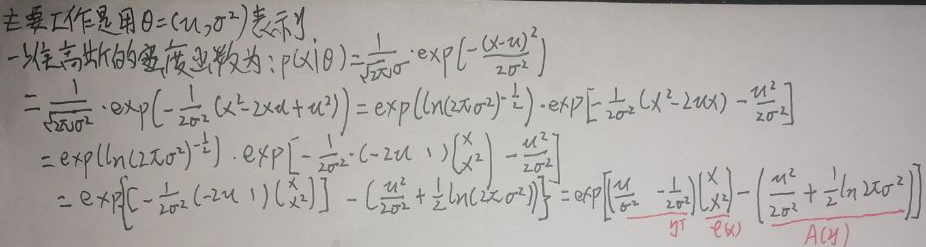
further:

according to the first sheet of the section [1.1 General form of the exponential family distribution] In the picture, here h(x)=1, and η, φ(x), A(η) are given in the above figure, so the density function of the one-dimensional Gaussian distribution is changed to the form of the exponential family distribution.
3 Logarithmic partition function and sufficient statistics
In the formula of exponential family distribution, φ(x) is called a sufficient statistic, and A(η) is called a logarithmic partition function. Let's study the relationship between A(η) and φ(x):

Take the partial derivative of η on the left and right sides of the formula ①:

According to the figure above
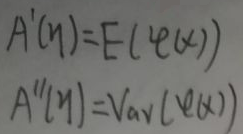
, the relationship between the logarithmic partition function A(η) and the sufficient statistic φ(x) is ① The first derivative of A(η) with respect to η is equal to the expectation of φ(x); ② The second derivative of A(η) with respect to η is equal to the variance of φ(x).
4 Maximum likelihood estimation and sufficient statistics
The following study uses MLE to study sufficient statistics φ(x) and η. First, suppose that the sample set is X=(x 1 ,x 2 ,...,x N ), set x i as a discrete random variable, and use MLE to find η:
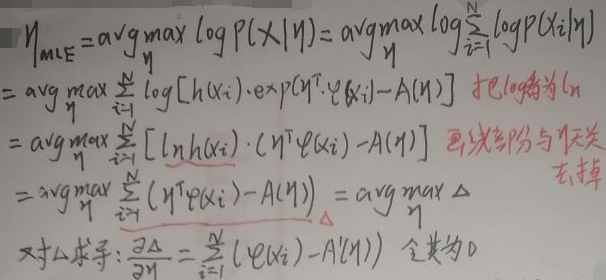
then:
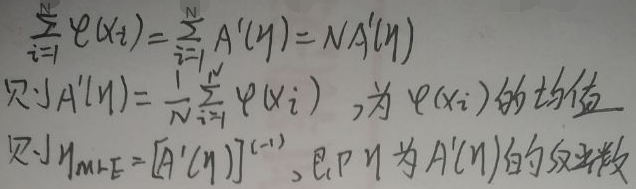
from the figure above: after using maximum likelihood estimation, The first derivative of A(η) with respect to η is equal to the mean value of the sufficient statistic φ(x); the parameter η is equal to the inverse function of the first derivative of A(η).
5 Entropy
Suppose the probability of occurrence of event x is p(x), then the amount of information is -log p(x), that is, the amount of information is inversely proportional to the probability. Entropy is a measure of the amount of information and uncertainty contained in a random variable, and the size is equal to the expectation of the amount of information, so the formula for entropy is:
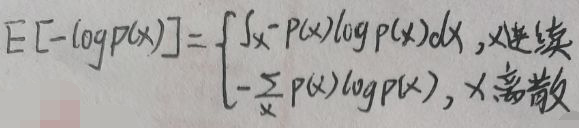
5.1 Maximum entropy ⇔ x obeys uniform distribution
This section proves that the maximum entropy ⇔ x obeys a uniform distribution. Assuming that x is discrete, the following is the proof process:

Therefore, the maximum entropy ⇔ x obeys a uniform distribution to prove.
5.2 Maximum entropy principle
According to the conclusion in section [5.1 Maximum entropy ⇔ x obeys uniform distribution], the maximum entropy is a quantitative description of equivalence. The principle of maximum entropy refers to including known experience, facts and information, without making any unknown assumptions, and treating unknown events as equal-probability events.
What are the known experiences, facts and information? For example, suppose the data set D=(x 1 ,x 2 ,…,x N ), let X be a discrete random variable, and X obeys the empirical distribution, that is: in the
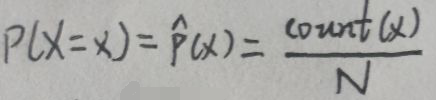
figure above, count(x) refers to the data set D The number of samples where x i = x. According to the above formula, the expected E(X) and the variance Var(X) can be calculated, but this is not the focus here, so it will not take time to find. In short, with the data set D, its expectation E(X) and variance Var(X) can be regarded as known facts. Let f(x) be any function whose independent variable is x, then E(f(x)) is also obtainable, so it can also be regarded as a known fact. In this way, the known experience, facts, and information are converted into mathematical quantities—expectations and variances.
What is required now is the distribution p(x) of x that maximizes entropy. Let x be a discrete random variable. The following is the detailed process:
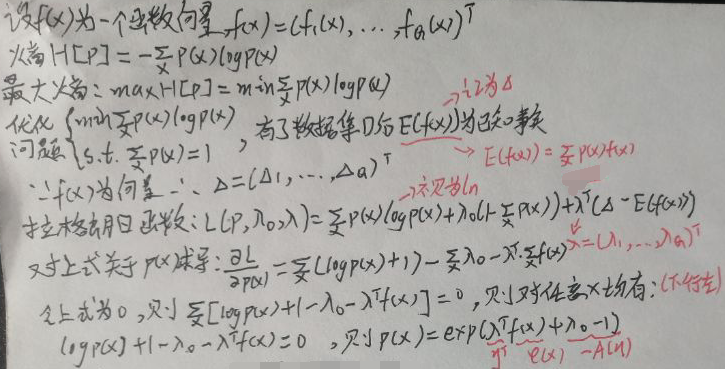
Compare the first picture in the section [1.1 General form of exponential family distribution], and look at the picture above. Lower right corner: Let η=(λ 0 ,λ) T , φ(x)=f(x), A(η)=1-λ 0 , h(x)=1.
In summary, the distribution p(x) of x that maximizes entropy is an exponential distribution.
END