Article Directory
Chapter 2 Structural Induction
The r relationship defined in the previous chapter is a function, but how do we prove it? Here is a semi-formal proof:
The r relationship is defined by a pair of constraints. The first constraint is an expression starting with f, and the result is uniquely determined by the right part of the expression. The second constraint is an expression starting with f, and the result is uniquely determined as t. Because an expression can only start with f or t, only one constraint will be applied, so the result is unique.
The above argument is quite persuasive, because it comes from the directly observable nature of an expression: whether the expression starts with f or t. Other relationships with B may not be so easy to prove. For example, it is not obvious to us that eval r is a function. The fundamental reason is that B is defined recursively, and there is no way to directly enumerate all interesting cases. So, in order to prove a more general argument, we have to use induction .
Mathematical induction is based on natural numbers. The usual certification process is:
- Prove that it is true when n = 0 (1).
- Assuming that n = m is true, then it can be deduced that the argument is also true when n = m + 1.
In most cases, in the proof we will consider, the natural number n is not provided for the set elements, but in the process of demonstrating that an expression belongs to a set, the expression can be derived based on the number of steps in the argument Out the natural number n we need.
Despite repeated as mathematical induction process to find a suitable natural number, we will use structural induction , which directly acts on the set of syntax elements defined, consistent with the basic principle of mathematical induction.
2.1 Elements of structural induction
Structural induction is used when proving a set that is not recursively defined. A set is fully defined only when there are atomic elements in the definition. These elements constitute the basic elements of inductive proof. The self-referential (recursive) element in the definition is the inductive element.
For example, we have the following definition:
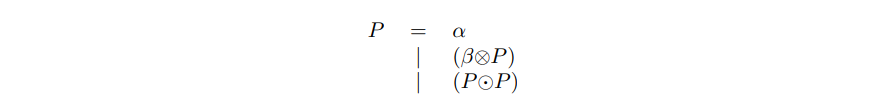
the members of P in the definition include α, (β ⊗ α), (α O・ α) and ((β ⊗ (β ⊗ α)) O・ (β ⊗ α)). Regarding the element of P, there is now an argument:
Theorem 2.1 : For any P, P contains equal numbers of β and ⊗
The truth and falsehood of this theorem are obvious. But because Theorem 2.1 makes all possible assertions about P, and P is defined recursively, it must be proved by structural induction.
Guidelines : If an argument contains all the elements of a recursively defined set, then structural induction is required.
The key to a correctly constructed inductive proof is that it can guarantee to cover the entire set. For example, the P set above, here is an example to illustrate Theorem 2.1
A proof of Theorem 2.1 :
-
Basic elements:
-
Element α
α contains 0 β and 0 ⊗, so the argument holds
-
-
Inductive elements:
-
Element (β⊗P)
In recursion, since P is a substructure of (β⊗P), P contains the same number (n) of β and ⊗. Therefore, (β⊗P) contains n+1 β and ⊗, the argument still holds
-
Elements (P1 O・ P2)
In recursion, P1 contains the same number (n1) of β and ⊗, and P2 also contains the same number (n2) of β and ⊗. Therefore, P1 O・ P2 contains n1+n2 β and ⊗, the argument still holds
-
The above proof has a canonical form. In the introduction, "by inducing the structure of P" encapsulates a model argument, which works as follows:
- The argument must be true for any P. Therefore, assume that an arbitrary P element is provided. If P has basic elements (that is, there is no self-referentiality in it), we prove how to immediately infer the argument based on the basic elements. If P is an inductive element (self-referential), then rely on the inductive method, assuming that the argument of P neutron structure is established, and then derive the argument. According to the principle of structural induction, this argument is applicable to any P (that is, the argument holds).
The proof of Theorem 2.1 contains a single basic element, because the definition of P contains only one basic element. The proof contains two inductive elements, because the definition of P contains two self-referential definitions.
Guidance : For a standard format for structural induction proof, the basic elements section should provide proof for each basic element in the set definition. Similarly, the inductive element part should provide proof for each inductive element in the set definition.
The standard format of structure induction proof plays a guiding role for both the prover and the reader. The prover develops the argument for each element one by one, while the reader can quickly check whether the entire proof process is standard, and can concentrate on checking the correctness of each element's proof.
Sometimes, in the basic element or the inductive element part, the segmentation element uses a standard other than the structural induction method. This segmentation method only distinguishes the deeply nested elements, so it is acceptable. A non-standard element segmentation must include all elements in an obvious way.
All proofs (including Theorem 2.1) have the following format:

The details in the proof depend on the argument. The following argument also includes all P elements and therefore has the same format as above.
Theorem 2.2 For any P, P contains at least one α
Exercise 2.2
Proof Theorem 2.2
answer
Proof as follows
-
Basic elements:
-
Element α
α contains 1 α, the argument is established
-
-
Inductive elements:
-
Element (β⊗P)
In recursion, P contains at least one α, so (β⊗P) contains at least one α, the argument still holds
-
Elements (P1 O・ P2)
In recursion, P1 contains at least one α, P2 also contains at least one α, the argument still holds
-
The certificate is complete.