[Programming Languages And Lambda calculi] 4.7~4.8 Some facts about Lambda calculus Paradigm History End Chapter 4

4.7 Some facts about Lambda calculus

When is an expression completely restored? Almost all expressions can be reduced by renaming variable names with → _n ^α , so → _n ^α cannot be included in the definition. Therefore, a completely reduced expression is an expression that cannot be reduced by → _n ^β → _n ^η .

concept:

• If an expression can no longer be reduced by → _n ^β → _n ^η , it is called a normal form.

• M has normal form N if M = _n N and N is normal form.

The function of normal form is the same as the result of Lambda calculus expression. If an expression has a normal form, it has one and only one normal form (which may be obtained through many different reductions). More precisely, → _n ^α renaming and modulo can only get one normal form.

Theorem 4.2 [Normal form] : If L = _n M, L = _n M, and M and N are both normal form, then M = _α N

As usual, = _{α is} the equivalent relationship generated by α compatible closure. Theorem 4.2 is easily proved by the Church-Rosser property:

***Theorem 4.3 [= _n represents the Church-Rosser relationship]***: If M = _n N, there is an L'such that M →→ _n L'and N →→ _n L'

As for = _r , the proof of this theorem depends on the prismatic nature of →→ _n .

Theorem 4.4 [→→ _n represents the prismatic property] : If L →→ _n M and L →→ _n N, there is an expression L'such that M →→ _n L'and N →→ _n L'

The single-step relation → _n does not satisfy the prismatic property, or even the slight distortion relation, such as the class-prismatic property of → _r . The reason is that → _n ^β can repeat reducible expressions. such as:

For the above two reduced expressions, no single-step relationship can reduce them to the same expression. In the next section, we will know that the way to solve this problem is to define a concept of parallel reduction around the sub-relation, so that the two ((λy.y) (λz.z)) sub-expressions on the left can be reduced at the same time . For now, we will not try to prove Theorem 4.4 for the time being. In the next chapter we will demonstrate the prismatic nature of associated languages.

Unlike the relational expression in B, the result of every expression is either f or t, and not every Lambda expression has a normal form. For example, there is no paradigm for Ω:

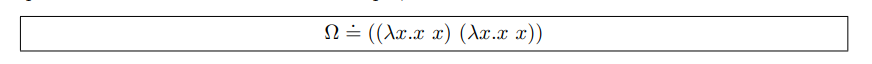
Even if an expression has a paradigm, there may be an infinite reduction order that can never become a paradigm, for example:

Therefore, Theorem 4.2 only guarantees that there is at most one normal form, but we have not found a way to it so far. Intuitively speaking, the above-mentioned infinite reduction problem makes us calculate the parameters of a function, but this parameter will not be used in the function body. This prompted us to the left most of the β or η about achieved Paradigm:
Katex the parse error: Got function '\ overline' with arguments NO AS AT subscript position. 3: → _ \ overline {G} relationships are known as well-ordered Reductions Relationship, it will find the paradigm under the premise of the existence of the paradigm.

Theorem 4.5 [Good Order Reduction ] : If and only if M →→_{$\overline{G}$} When N, N is the normal form of M.

Good order of about (normal-order reduction) is also referred to name call (call-by-name).

Although a well-ordered reduction will find the paradigm when the paradigm exists, almost no programming language uses this reduction relationship. Because the good order is effective but very slow. For example, in the → _n relation that proved the non-prismatic nature in the previous paragraph, the reduction on the left corresponds to the good order, and the reduction on the right will get the same function in fewer steps. .

In any case, because we have the concept of a unique normal form, the question comes to whether we can try to define an eval _n function by defining eval _r : evaln (M) =? N if M = n N and N is a normal form eval_n(M)\overset{\text{?}}{=}N \ if\ M =_nN\ and \ N\ is\ a\ normal\ form
$$eva{l}_n(M)\stackrel{\text{?}}{=}NifM{=}_{n}NandNisanormalform\; The$$
above definition is inaccurate for α-renaming, but there is a deeper problem. As we have seen, similarmkandYthis function, they behave the same way, but not with each other about technology. In the next chapter, we will explore ways to solve this problem.

Exercise 4.15

Prove that ((λx.xx) (λx.xx)) does not have a paradigm.

answer

Apply β good order reduction to ((λx.xx) (λx.xx)) :

((λx.x x) (λx.x x)) β ((λx.x x) (λx.x x))

Since after β good order reduction, we get the same expression, this reduction will not loop, so we cannot get a normal form expression. So ((λx.xx) (λx.xx)) does not have a normal form.

4.8 History

Slightly before Turning invented Turning machines, Church invented the Lambda calculus.

Barendregt made a comprehensive study of Church's Lambda calculus as a logical system. Many conventions dealing with terminology originated from Barendregt. Although he did not regard Lambda calculus as a programming language for calculus, his book provides many techniques for calculus.