Foreword
The quality of the pros and cons of an algorithm will determine the time a program runs, and space. Maybe when a small amount of data when this effect is not obvious, but when there is a huge amount of data, the algorithm is good or bad performance difference will bring out the bad days to do. It can be said directly affect the height and breadth of a product. Every programmer wants to use the best algorithm to solve the problem, we look forward to write their own code is simple and efficient. But how to judge the quality of an algorithm do? Time complexity and space complexity is a good standard.
1. Time complexity
1.1 concept
Computational effort required for execution of the algorithm is that we often say that the time complexity. This value is not necessarily equal to the basic number of executions next to introduce. An approximate value of statistical significance.
1.2 Basic execution times T (n)
According to calculations, the algorithm resulting in the input data amount, when the actual execution times n. The exact value of specific values, there are mathematical sense.
1.3 Time Complexity
The time complexity of the progressive number of executions obtained substantially removing coefficient, the constant term and the like. Notation with a large O. That is, as the amount of surge data, various coefficients and constant term has been generally can not substantially affect the number of times of execution of the algorithm. Calculating coefficients and constant term for the time complexity meaningless
1.4 illustrates
- T (n) = 2: This function is performed a total of two statements, performing the basic frequency is 2; the time complexity is O (1): The basic function of the number of times of performing only the constant term, the time complexity is O (1)
void test(int n)
{
int a;
a = 10;
}
- T (n) = 2n: The total cycle function n times, each execution of statement 2, the execution times of substantially 2n. Time complexity coefficient discarded as O (n)
void test(int n)
{
int cnt;
for (cnt = 0; cnt < n; cnt++) {
int a;
a= 10;
}
}
- T (n) = 2 * (1 + 2 + 3 + 4 + ... + n) + 1 = 2 * (1 + n) * n / 2 + 1 = n ^ 2 + n + 1. Because the total execution (1 + 2 + 3 + 4 + ... + n) cycles, each cycle execution statement 2, after all cycles, and finally a statement executed, the execution count above; time complexity is O (n ^ 2), because the constant term 1 and n is ignored, when the amount of data which the sharp increase, the number of executions for the curve is almost no effect
void test(int n)
{
int cnt1, cnt2;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = cnt1; cnt2 < n; cnt2++) {
int a;
a = 10;
}
}
a = 11;
}
- T (n) = 2 * logn since each loop executes the statement 2, total cycles performed logn; time complexity is O (logn), ignored factor 2
void test(int n)
{
int cnt;
for (cnt = 1; cnt < n; cnt *= 2) {
int a;
a = 10;
}
}
- T (n) = n * logn * 2 since each statement cycle 2, a total of n * logn execution cycles; time complexity of O (nlogn), ignored factor 2
void test(int n)
{
int cnt1, cnt2;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = 1; cnt2 < n; cnt2 *= 2) {
int a;
a = 10;
}
}
}
- T (n) = 2 * n ^ 3 because each statement cycle 2, n ^ 3 total execution cycles; time complexity of O (n ^ 3), the coefficient ignored 2
void test(int n)
{
int cnt1, cnt2, cnt3;
for (cnt1 = 0; cnt1 < n; cnt1++) {
for (cnt2 = 0; cnt2 < n; cnt2++) {
for (cnt3 = 0; cnt3 < n; cnt3++) {
int a;
a = 10;
}
}
}
}
- Fibonacci number of recursive implementation, each call to the function will break down, and then again twice to call the function. Therefore, the time complexity is O (2 ^ n)
int test(int n)
{
if (n == 0 || n == 1) {
return 1;
}
return (test(n-1) + test(n-2));
}
1.5 Comparison of time complexity
O(1) < O(log2n) < O(n) < O(nlog2n) < O(n^2) < O(n^3) < O(2^n) < O(n!) < O(n^n)
2. Space complexity
2.1 Concepts
An algorithm occupies the space include:
- The space occupied by the program itself
- Output variable input space occupied
- Dynamically allocated temporary space, usually auxiliary variables
Input data footprint depends only on the problem itself, and algorithm-independent. We call space complexity of the algorithm is a temporary occupation measure of the size of the storage space during operation, the third term. Generally speaking, as long as the algorithm is not related to the spatial distribution and the dynamic recursive space required stack space complexity is usually 0 (1).
2.2 illustrates
- S (n) = O (1). Spatial complexity is O (1), because only a, b, c, cnt four temporary variable. Irrespective of the number and size of temporary variables and input data.
int test(int n)
{
int a, b, c;
int cnt;
for (cnt = 0; cnt < n; cnt++) {
a += cnt;
b += a;
c += b;
}
}
- S (n) = O (n). Spatial complexity is O (n), because each recursive creates a new temporary variable a. And co-recursive n times.
int test(int n)
{
int a = 1;
if (n == 0) {
return 1;
}
n -= a;
return test(n);
}
3. The function of progressive growth and progressive time complexity
In the example above, we usually discard and the constant term. This is because when a surge input, infinite close timing, and the constant term is not able to affect the execution count curve. Different curves and the constant term will coincide completely. I did a line graph to compare the surge time when the input value n, n ^ 2, and a graph curve 2n ^ 2 + 100. It can be seen that, when the data surge, and the constant term statistics are no longer significant for time complexity, the two curves overlap almost completely.
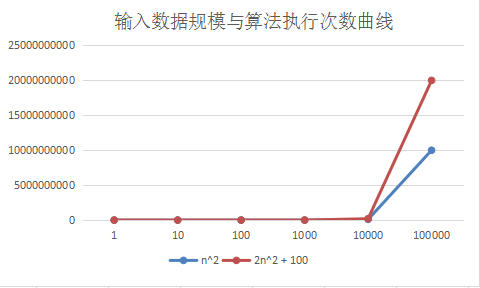
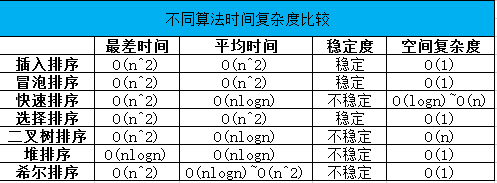
4. The time complexity of the algorithm & different spatial complexity
Below is a table I did, sort of a different time sorting algorithm complexity and space complexity for your reference:
Thanks for reading, recommend everyone likes please help point. Behind will continue the exciting content, so stay tuned!
CAUTION:
This article original, welcome to reprint learning
Reproduced, please indicate in a prominent position:
Bloggers ID: CrazyCatJack
Original Bowen link address: https://www.cnblogs.com/CrazyCatJack/p/12657097.html