由均值向量\(\mu \in \mathbb{R}^{n}\)和协方差阵\(\Sigma \in \mathbb{R}^{n \times n}\)参数化的\(n\)维多元正态分布或多元高斯分布记作\(\mathcal{N}(\mu, \Sigma)\)。其中协方差矩阵\(\Sigma \in \mathbb{R}^{n \times n}\)是对称半正定矩阵。它的密度函数为,
\[ \begin{equation} p(x ; \mu, \Sigma)=\frac{1}{(2 \pi)^{n / 2}|\Sigma|^{1 / 2}} \exp \left(-\frac{1}{2}(x-\mu)^{T} \Sigma^{-1}(x-\mu)\right) \end{equation} \]
一个服从多元正态分布的随机向量的均值,即$X\sim \mathcal{N}(\mu, \Sigma) $,有
\[ \mathrm{E}[X]=\int_{x} x p(x ; \mu, \Sigma) d x=\mu \]
为了引出一个服从多元正态分布的协方差阵,首先(作为方差的推广)定义一个的随机向量的协方差阵为,
\[ \begin{equation} \operatorname{Cov}(Z)=\mathrm{E}\left[(Z-\mathrm{E}[Z])(Z-\mathrm{E}[Z])^{T}\right] \end{equation} \]
而且可以验证下面这种定义和上面滴是等价的,
\[ \begin{equation} \operatorname{Cov}(Z)=\mathrm{E}\left[Z Z^{T}\right]-(\mathrm{E}[Z])(\mathrm{E}[Z])^{T} \end{equation} \]
若$X\sim \mathcal{N}(\mu, \Sigma) $ ,则有, \[\operatorname{Cov}(X)=\Sigma\]
直观印象
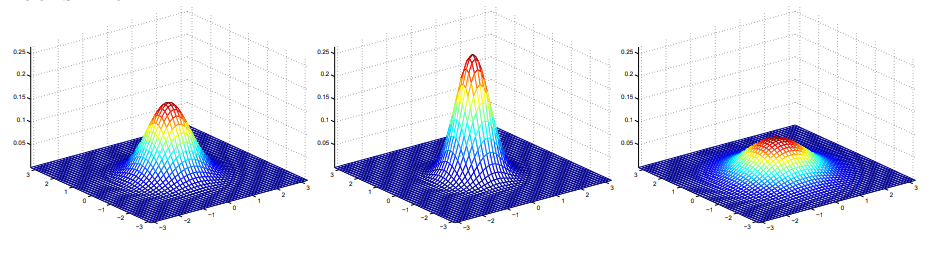
上面从左向右三个图分别表示均值为零,方差为单位矩阵,0.6倍单位矩阵,两倍单位矩阵的多元二维多元正态分布密度图。可以看到,方差协方差矩阵越大,分布越平坦。
下面三个图展示两个变量相关系数越来越大时,二元正态分布密度图。可以看到相关系数越大,越向45度角倾斜。这从下面相应的等高线图中可以更明显地看出。这三个相关系数矩阵,也分别列出来如下,


\[ \Sigma=\left[\begin{array}{ll}{1} & {0} \\ {0} & {1}\end{array}\right] ; \Sigma=\left[\begin{array}{cc}{1} & {0.5} \\ {0.5} & {1}\end{array}\right] ; \Sigma=\left[\begin{array}{cc}{1} & {0.8} \\ {0.8} & {1}\end{array}\right]. \]
下面再来一组带有负相关系数的等高线图。三个协方差矩阵分别为,

\[ \Sigma=\left[\begin{array}{rr}{1} & {-0.5} \\ {-0.5} & {1}\end{array}\right] ; \Sigma=\left[\begin{array}{rr}{1} & {-0.8} \\ {-0.8} & {1}\end{array}\right] ; \Sigma=\left[\begin{array}{rr}{3} & {0.8} \\ {0.8} & {1}\end{array}\right] \]