Kalman Filter简单介绍
卡尔曼滤波是一种用于估计含有不确定因素的动态系统状态的优化算法,其最初由Rudolf E. Kálmán于1960年代提出。该算法广泛应用于各种工程和科学领域,特别是在控制系统、导航、自动驾驶、信号处理等方面。
卡尔曼滤波是基于概率推理的方法,它通过融合系统的预测模型和测量数据来估计系统的状态,尤其适用于带有噪声的动态系统。在每个时间步骤中,卡尔曼滤波会做出两个主要步骤:
- 预测步骤(预测阶段): 根据系统的动态模型和前一个状态的估计,预测当前时刻的状态。这个预测考虑了系统的物理规律以及外部输入。
- 更新步骤(更新阶段): 在收到测量数据后,卡尔曼滤波会结合预测的状态和实际测量值,通过加权平均的方式来修正状态估计,从而获得更准确的状态估计值。卡尔曼滤波会根据测量数据的可靠性自动调整权重,对于更可信的数据,其影响会更大。
想象你在驾驶一辆车,你有车速表可以告诉你当前的速度,但是它可能有些抖动或者不准确。同时,你也有眼睛可以看到路上的实际情况,比如你正朝着一个目标行驶。现在,卡尔曼滤波就像一个聪明的司机,他会结合车速表的估计和你眼睛看到的实际情况,以一种明智的方式修正你的速度估计。这样,你的驾驶速度就更准确了。当然卡尔曼滤波的作用可不限于估计车速,它在现代科学和工程领域有着举足轻重的作用。导航系统中飞行器的位置和姿态估计、雷达跟踪目标、视频目标跟踪、信号去噪、物体定位中卡尔曼滤波都能发挥作用。你甚至能实时得到女朋友的最优重量估计(如果有的话)。
引入预测公式
在一维空间中有辆小车向前移动,加速度为 f t m \frac{f_t}{m} mft,t时刻瞬时速度为 v t v_t vt,t时刻小车位置为 x t x_t xt。按照初中知识,小车的位置公式如下:
x t = x t − 1 + v t ⋅ △ t + 1 2 f t − 1 m △ t 2 x_t = x_{t-1} + v_t·\triangle t + \frac{1}{2}\frac{f_{t-1}}{m}\triangle t^2 xt=xt−1+vt⋅△t+21mft−1△t2
小车的速度公式如下:
v t = v t − 1 + f t − 1 m △ t v_t = v_{t-1} + \frac{f_{t-1}}{m}\triangle t vt=vt−1+mft−1△t
现在假设小车状态用 X t = [ x t , v t ] T X_t=[x_t,v_t]^T Xt=[xt,vt]T表示,上面两个公式可用如下矩阵表示
X t = [ x t v t ] = [ 1 △ t 0 1 ] ∗ [ x t − 1 v t − 1 ] + [ 1 2 △ t 2 △ t ] ⋅ f t − 1 m X_t = \begin{bmatrix} x_{t} \\ v_{t}\end{bmatrix}= \begin{bmatrix} 1 & \triangle t \\ 0 & 1 \end{bmatrix} * \begin{bmatrix} x_{t-1} \\ v_{t-1} \end{bmatrix} + \begin{bmatrix} \frac{1}{2}\triangle t^2 \\ \triangle t \end{bmatrix}·\frac{f_{t-1}}{m} Xt=[xtvt]=[10△t1]∗[xt−1vt−1]+[21△t2△t]⋅mft−1
假设 F = [ 1 △ t 0 1 ] , B = [ 1 2 △ t 2 △ t ] , U t = f t − 1 m 假设F = \begin{bmatrix} 1 & \triangle t \\ 0 & 1 \end{bmatrix}, B=\begin{bmatrix} \frac{1}{2}\triangle t^2 \\ \triangle t \end{bmatrix} ,U_t = \frac{f_{t-1}}{m} 假设F=[10△t1],B=[21△t2△t],Ut=mft−1
则上述矩阵表达转化为:
X t = F ∗ X t − 1 + B U t − 1 X_t = F*X_{t-1}+BU_{t-1} Xt=F∗Xt−1+BUt−1
这里面的 F F F便是状态转移矩阵。但是这个预测方程难免受到误差的影响(例如路面不平),所以此时的 X t X_t Xt不是最优估计值,因此改为 X ^ − \hat{X}^- X^−,其中-号表示先验,并没有加入动态测量的数据,因此并不准确。
据此,我们可以引入卡尔曼滤波的五大核心公式。
Kalman Filter五大核心公式
预测部分:
X ^ t − = F X ^ t − 1 + B U t − 1 \hat{X}^-_t = F \hat{X}_{t-1} + BU_{t-1} X^t−=FX^t−1+BUt−1
P t − = F P t − 1 F T + Q P_t^- = FP_{t-1}F^T+Q Pt−=FPt−1FT+Q
更新部分:
K t = P t − H T ( H P t − H T + R ) − 1 K_t = P^-_tH^T(HP^-_tH^T+R)^{-1} Kt=Pt−HT(HPt−HT+R)−1
X ^ = X t − + K t ( Z t − H X ^ t − ) \hat{X} = X^-_t+K_t(Z_t-H\hat{X}_t^-) X^=Xt−+Kt(Zt−HX^t−)
P T = ( I − K t H ) P t − P_T=(I-K_tH)P^-_t PT=(I−KtH)Pt−
现在解释下各个参数的意义——
X ^ t − \hat{X}^-_t X^t−:t时刻的先验预测状态,并不准确。
P T − P_T^- PT−:预测误差的协方差矩阵,表示t时刻系统的不确定性。

F F F:状态转移矩阵,有的系统不像小车运行那样能归纳出F,如测量温度(见matlab实现)
U t U_t Ut:t时刻外部对系统的已知影响
Q Q Q:过程噪声的协方差矩阵
R R R:观测噪声的协方差矩阵
K t K_t Kt:卡尔曼增益,权衡预测状态协方差P和观测状态协方差R的大小来决定二者的重要程度,如果更相信预测模型,则 K t K_t Kt变小,如果更相信观测模型,则 K t K_t Kt变大。另外,卡尔曼增益包含了所有的预测变量,所以在更新时能够同时更新所有的变量。
Z t Z_t Zt:实际观测值,有如下公式: Z t = H X t + V Z_t=HX_t+V Zt=HXt+V,其中 H H H是观测矩阵, V V V是观测噪声。这个公式是多传感器融合的核心公式,也叫做观测方程。当只观测位置时,则 H = [ 1 , 0 ] H=[1, 0] H=[1,0],得到的 Z t Z_t Zt是一个数值。
一定要注意观察迭代公式以及里面带有负号上标的符号
matlab实现1:小车运动轨迹
%卡尔曼滤波估计小车的运动,这是一个含有不确定性噪声的动态系统,需要做最优估计
clc;
clear;
Z = (1:100); %假设小车理想情况下是匀速运动,每隔1s观测一次。后面会加上噪声
noise = randn(1,100);
Z = Z + 20*noise; %观测系统的小车的状态,可以适当突出噪声演示kalman的作用
X = [0; 0]; %预测的初始值,设为多少不重要
P = [1 0; 0 1]; %预测系统的初始协方差,设为多少不重要
F = [1 1; 0 1]; %状态转移矩阵,由于1s观测一次,delta_t为1
Q = [0.0001 0; 0 0.0001]; %相信观测转移矩阵,误差设置的较小
H = [1 0]; %观测矩阵,只观测到小车位置
R = 1; %由于noise设置为标准正态分布,这里观测的协方差设置为1
X_data = zeros(500, 2); %存储小车最优状态估计,初始设置为0,后面会不断更新,500行数据需要迭代500次完成更新
for t=1:500
X_ = F * X;
P_ = F * P * F' + Q;
K = P_ * H' / (H * P_ * H' + R);
X = X_ + K * (Z(t) - H * X_);
X_data(t, 1) = X(1);
X_data(t, 2) = X(2);
P = (eye(2) - K * H) * P_;
end
plot(X_data(:, 1), 'b-');
xlabel('时间/s')
ylabel('小车位置/m')
title('kalman filter');
hold on;
plot(Z, 'k+');
legend('kalman最优估计值', '带噪声的观测值');
hold off;
由于kalman是个动态最优估计算法,所以不是最终输出一个最优值,而是每次增加一次观测后都进行后验估计,可以把它们打印出来进行观察。
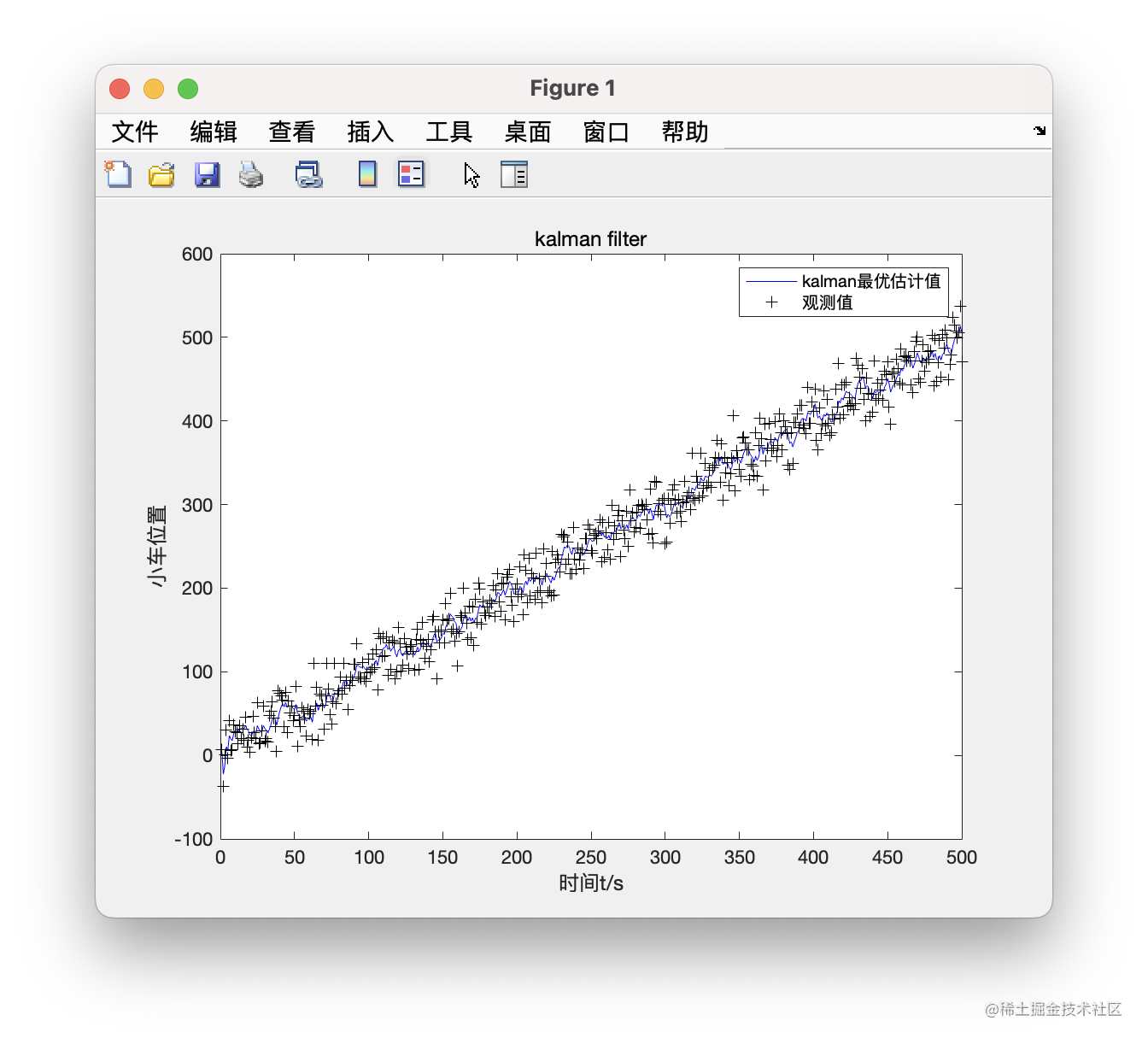
关于小车位置的估计,可以看到最优估计是在分布的最中央,这也是我们期望的。
matlab实现2:最优温度估计
clc;
clear;
Z = 24 + randn(1, 4000); %假设测量值是24加上高斯噪声N(0,1)
X = zeros(1, 4000); %最优估的初始值,后面会迭代更新
P = zeros(1, 4000); %预测模型的协方差,注意这里并不是一个对称矩阵
Q = 0.001; %相信观测转移矩阵,误差设置的较小
R = 1; %观测模型的协方差
for t=2:4000
X_(t) = X(t-1);
P_(t) = P(t-1) + Q;
K(t) = P_(t) / (P(t) + R);
X(t) = X_(t) + K(t) * (Z(t) - X_(t));
P(t) = (1 - K(t)) * P_(t);
end
figure;
plot(Z, 'k+');
hold on;
plot(X, 'b-', 'linewidth', 1);
hold on;
plot(24*ones(1, 4000), 'r-', 'linewidth', 1);
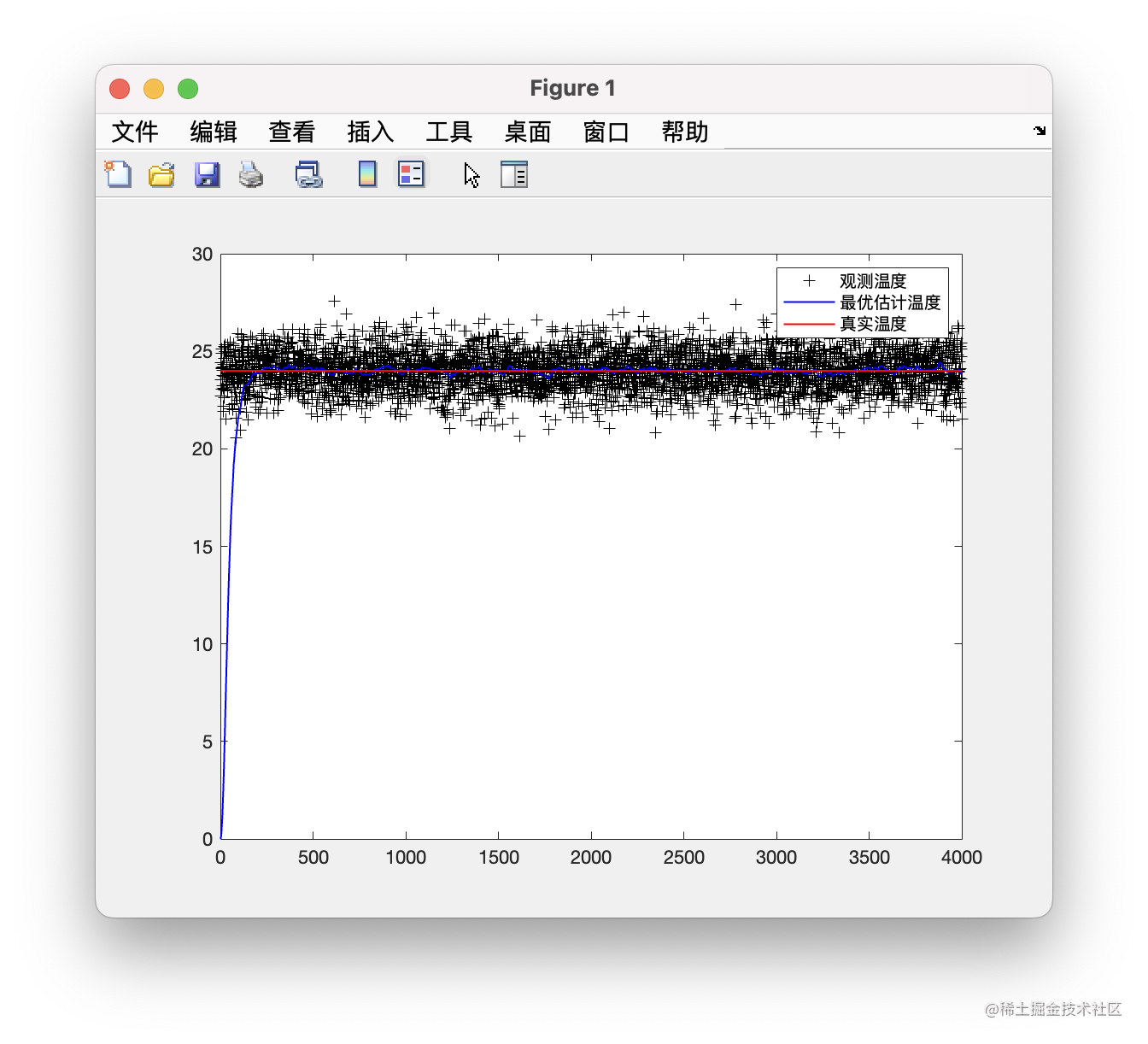
让我们放大一下部分图像:
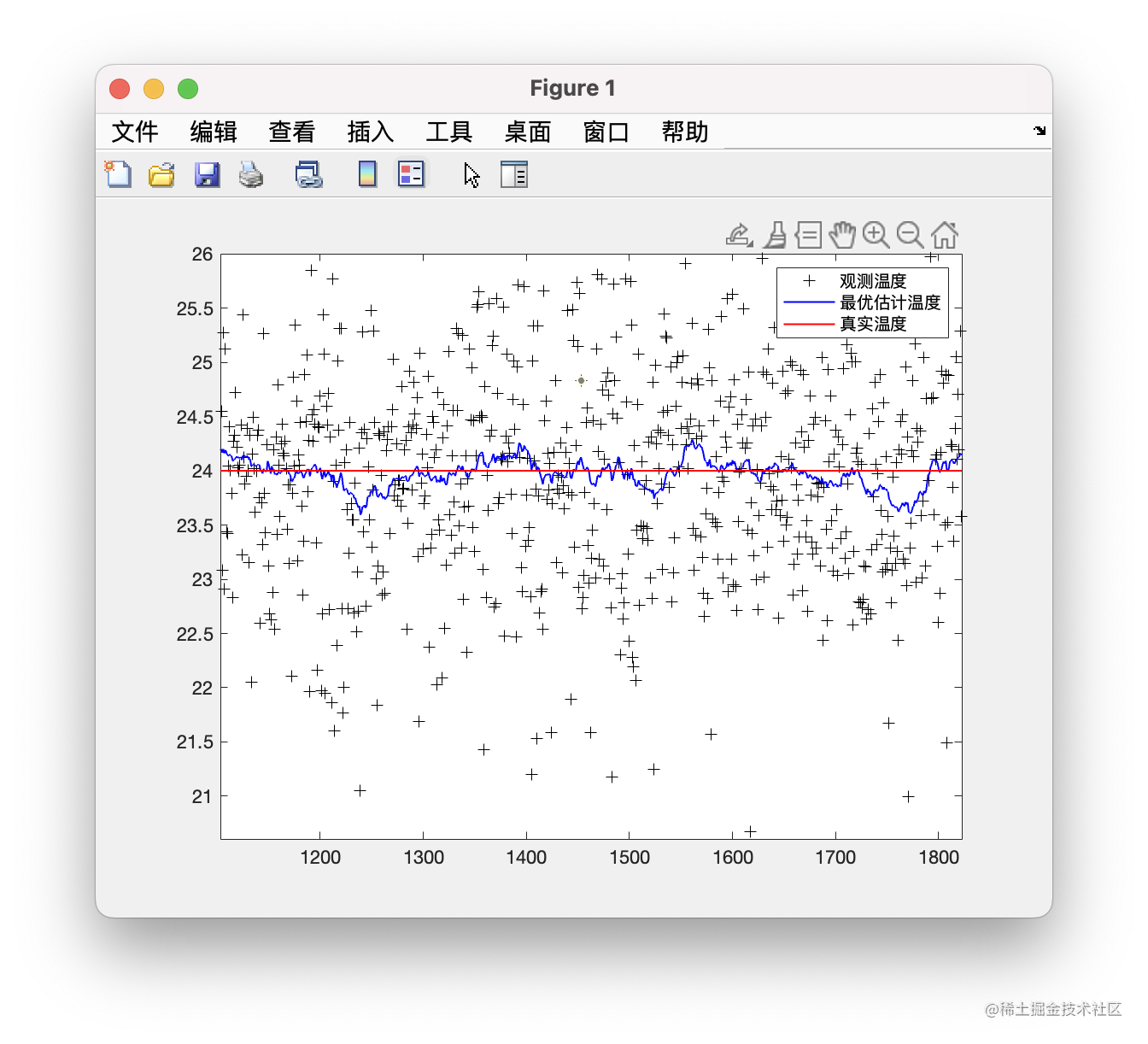
可见,最优估计值是能够接近真实值的(假设某化学试剂的真实温度是24,但是不能用温度计放入液体中直接测量,假设可以在液体上方测量,而在周围温度受到扰动,这就是所谓的观测值带有噪声,我们需要尽可能消除这些噪声,得到温度的最优估计)。
如果卡尔曼滤波只能做线性估计,那它的意义将大大降低。卡尔曼滤波更重要的点在于数据融合!!!。但最经典的卡尔曼滤波做数据融合只能作为背景板,现在有各种卡尔曼变体在数据融合方面表现优秀,如KEF、UEF等。
上述观点如果改进还请各位大佬斧正,整理不易,喜欢的话就点个赞吧!