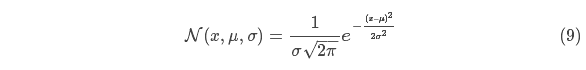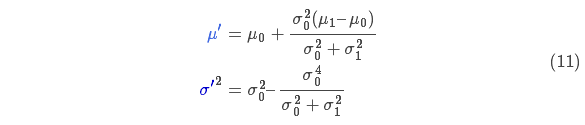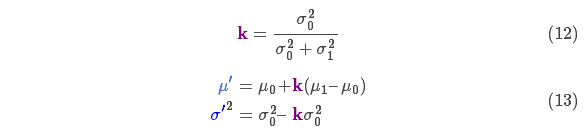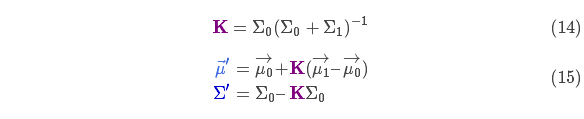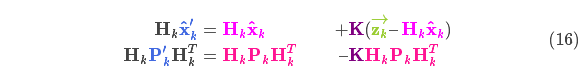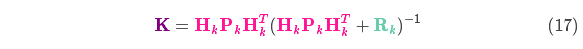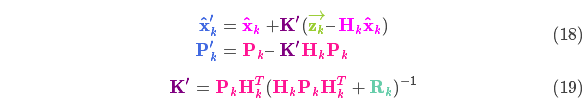卡尔曼滤波理论讲解与实例（matlab和python）

理论讲解

卡尔曼滤波属于线性滤波器，它可以在多元不确定信息下通过融合多个信息源来得到一种最优的状态估计。卡尔曼滤波在连续变化的线性系统中表现是非常出色的，因为它考虑了系统过程中存在的一些干扰，比如模型预测干扰 $Q$和测量过程干扰 $R$，因此，即使系统中伴随着一些干扰，卡尔曼滤波器也可以比较准确的计算出实际的状态，并且可以对系统未来的运动状态做出合理的预测。卡尔曼滤波器的前提条件是系统是线性高斯系统，线性高斯系统需要从两个方面的理解：

1. 线性：运动方程、观测方程是线性的

2. 高斯：系统噪声服从零均值的高斯分布

综合来说也就是说高斯分布的噪声在经过状态转移之后仍然保持高斯分布。如果不满足这个线性这个前提条件，就需要使用扩展卡尔曼滤波（extended kalman filter ，EKF）和无迹（损）卡尔曼滤波了（Unscented Kalman Filter ，UKF）来代替了。另外卡尔曼滤波器也假设状态是符合正态分布的。

如下图2.15所示，卡尔曼滤波器的信息源一方面来自传感器检测出的车辆状态信息 $\hat{z_k}$，另一方面来自数学模型预测出的车辆状态信息 $\hat{x_k}$，但这两方面信息源都只是间接的预测，并且伴随着一些不确定和不准确性，如果使用上所有可用的信息源，那么就能得到一个比单一的任何信息源估计更好的结果 $\hat{x_k}'$。卡尔曼滤波通过两个高斯分布相乘，就可以把多个不确定信息源融合在一起。传感器检测的车辆状态信息 $\hat{z_k}$在某种情况下符合一个高斯正太分布，预测模型计算出的车辆状态信息也 $\hat{x_k}$符合一个高斯正太分布，而后将这两个独立的高斯分布相乘就会得到一个新的高斯分布 $\hat{x_k}'$。新的高斯分布就是原来两个高斯分布重叠的区域，其均值就代表着最优的状态估计。

卡尔曼滤波的实质是预测的车辆状态和测量的车辆状态两个高斯分布相乘的到新的高斯分布，该过程最后可以凝练成五个核心公式：

预测公式：

$\hat x_k=F_k \hat x_{k-1} + B_k \vec u_k\\ P_k=F_kP_{k-1}F^T_k+Q_k$
更新公式：

$K' = P_kH^T_k(H_kP_kH^T_k+R_k)^{-1}\\ \hat x'_k = \hat x_k+K'(\vec {z_k}-H_k\hat x_k)\\ P'_k=P_k-K'H_kP_k$
其中 $\hat{x_k}$为 $k$时刻的状态向量， $F_k$为状态转移矩阵，表示将 $k-1$时刻的状态向量转移至t时刻的状态向量， $B_k$是输入控制矩阵，代表着将控制向量 $\hat{u_k}$映射到状态向量上，统一控制向量 $\hat{u_k}$和状态向量之间 $\hat{x_k}$的关系， $\hat{u_k}$代表着控制向量，如加速度，角加速度等， $P_k$为状态向量的协方差矩阵，代表着状态向量每个元素之间的关系， $Q_k$表示预测状态的高斯噪声的协方差阵，它用来衡量模型的准确度，模型越准确其值越小， $\vec {z_k}$为传感器测量值的状态向量，也就是传感器的测量结果， $H_k$ 为转换矩阵，他将状态向量 $\hat{x_k}$映射到测量值所在的向量空间 $\vec {z_k}$， $R_k$为测量值的高斯噪声的协方差阵，代表着传感器测量的误差。

---

公式推导

那卡尔曼滤波公式的五个公式是如何推导的呢？

用均值和方差描述物体状态

怎么去描述某一时刻物体的状态呢? 状态 $\hat{x_k}$可以包含多个变量，代表任何你想表示的信息， 我们用均值和方差来表示某一时刻的状态，为啥是这两个呢? 均值就是我们定义要知道的一些变量状态，例如位置，速度，体积，温度等等。它表示随机分布的中心，即最可能的状态。方差表示一种偏离均值的程度，他可以告诉我们更多信息，利用其中一个变量值告诉我们其它变量可能的值。例如，位置和速度的关系。我们基于旧的位置来估计新位置。如果速度过高，我们可能已经移动很远了。如果缓慢移动，则距离不会很远。跟踪这种关系是非常重要的，因为它带我们更多的信息：其中一个测量值告诉了我们其它变量可能的值，这就是卡尔曼滤波的目的，尽可能地在包含不确定性的测量数据中提取更多信息！这种相关性用协方差矩阵来表示。矩阵中的每个元素 $\Sigma_{ij}$ 表示第 $i$个和第 $j$个状态变量之间的相关度。（协方差矩阵是一个对称矩阵，这意味着可以任意交换 $i$ 和 $j$）。协方差矩阵通常用“ $\Sigma$”来表示，其中的元素则表示为“ $\Sigma_{ij}$ ”。

所以在时刻 $k$ 物体的状态为 ：均值 $\hat{x_k}$和协方差矩阵 $P_k$ 。
$\hat{x_k}=\left[ \begin{matrix} position \\ velocity \\ \end{matrix} \right] \quad\quad\quad P_k=\left[ \begin{matrix} \Sigma_{pp}&\Sigma_{pv} \\ \Sigma_{vp}&\Sigma_{vv} \\ \end{matrix} \right]$

状态转移矩阵 $F$表示预测

接下来，我们需要根据当前状态（ $k-1$ 时刻）来预测下一状态（ $k$ 时刻），怎么去预测呢?

我们可以用矩阵 $F_k$来表示这个预测过程。这个 $F_k$就是根据运动学或者动力学等物理公式得到的内在关系或者规律。记住，我们并不知道对下一状态的所有预测中哪个是“真实”的，但我们的预测函数并不在乎。它对所有的可能性进行预测，并给出新的高斯分布。

它将我们原始估计中的每个点都移动到了一个新的预测位置，如果原始估计是正确的话，这个新的预测位置就是系统下一步会移动到的位置。那我们又如何用矩阵来预测下一个时刻的位置和速度呢？下面用一个基本的运动学公式来表示：矩阵表示
$p_k=p_{k-1}+\Delta tv_{k-1}\\ v_k=\quad\quad \quad\quad v_{k-1}$
或者表示为
$\hat x_k=\left[ \begin{matrix} 1&\Delta t \\ 0&1 \\ \end{matrix} \right] \hat x_{k-1}\\ =F_k \hat x_{k-1} \quad \quad$
现在，我们有了一个预测矩阵来表示下一时刻的状态，但是，我们仍然不知道怎么更新协方差矩阵。此时，我们需要引入另一个公式，如果我们将分布中的每个点都乘以矩阵 $A$，那么它的协方差矩阵会 $\Sigma$怎样变化呢？很简单，下面给出公式：
$Cov(x)=\Sigma\\ Cov(Ax)=A\Sigma A^T$
　　结合上面两个方程得到：
$\hat x_k=F_k \hat x_{k-1}\\ P_k = F_k P_{k-1} F^T_k$

外部控制变量 $u_k$

有时候，我们并没有捕捉到一切信息，可能存在外部因素会对系统进行控制，带来一些与系统自身状态没有相关性的改变。以火车的运动状态模型为例，火车司机可能会操纵油门，让火车加速。相同地，在我们机器人这个例子中，导航软件可能会发出一个指令让轮子转向或者停止。如果知道这些额外的信息，我们可以用一个向量 $\vec{u_k}$来表示，将它加到我们的预测方程中做修正。
　　假设由于油门的设置或控制命令，我们知道了期望的加速度 $a$根据基本的运动学方程可以得到：
$p_k = p_{k-1} + \Delta t v_{k-1} + \frac1 2 a (\Delta t)^2\\ v_k = \quad \quad \quad \quad \quad v_{k-1} + a \Delta t\\$
以矩阵的形式表示就是：
$\hat x_k = F_k \hat x_{k-1}+\left[ \begin{matrix} \frac{\Delta t^2} {2}\\ \Delta t \\ \end{matrix} \right] a \\ =F_k \hat x_{k-1} + B_k \vec u_k$
$B_k$称为控制矩阵， $\vec{u_k}$称为控制向量（对于没有外部控制的简单系统来说，这部分可以忽略）。让我们再思考一下，如果我们的预测并不是100%准确的，该怎么办呢？

外部干扰 $Q_k$

如果这些状态量是基于系统自身的属性或者已知的外部控制作用来变化的，则不会出现什么问题。 但是，如果存在未知的干扰呢？例如，假设我们跟踪一个四旋翼飞行器，它可能会受到风的干扰，如果我们跟踪一个轮式机器人，轮子可能会打滑，或者路面上的小坡会让它减速。这样的话我们就不能继续对这些状态进行跟踪，如果没有把这些外部干扰考虑在内，我们的预测就会出现偏差。在每次预测之后，我们可以添加一些新的不确定性来建立这种与“外界”（即我们没有跟踪的干扰）之间的不确定性模型：原始估计中的每个状态变量更新到新的状态后，仍然服从高斯分布。我们可以说 $\hat{x}_{k-1}$每个状态变量移动到了一个新的服从高斯分布的区域 $\hat{x}_{k}$，协方差为 $Q_k$。换句话说就是，我们将这些没有被跟踪的干扰当作协方差为的噪声 $Q_k$来处理。这产生了具有不同协方差（但是具有相同的均值）的新的高斯分布。

我们通过简单地添加 $Q_k$得到扩展的协方差，下面给出预测步骤的完整表达式：
$\hat x_k=F_k \hat x_{k-1} + B_k \vec u_k\\ P_k=F_kP_{k-1}F^T_k+Q_k$
由上式可知，新的最优估计 $\hat x_{k}$是根据上一最优估计 $\hat x_{k-1}$预测得到的，并加上已知外部控制量 $\vec u_k$的修正。而新的不确定性 $P_k$由上一不确定 $P_{k-1}$性预测得到，并加上外部环境的干扰 $Q_k$。

这里，我们对系统可能的动向有了一个模糊的估计，用均值 $\hat{x_k}$和协方差矩阵 $P_k$来表示。如果再结合传感器的数据会怎样呢？

用测量值( $\vec {z_k}，R_k$)来修正估计值

我们可能会有多个传感器来测量系统当前的状态，哪个传感器具体测量的是哪个状态变量并不重要，也许一个是测量位置，一个是测量速度，每个传感器间接地告诉了我们一些状态信息。注意，传感器读取的数据的单位和尺度有可能与我们要跟踪的状态的单位和尺度不一样，我们用矩阵 $H_k$ 来转换传感器的数据，使它的单位和尺度和我们的状态 $x_k$一致

我们可以计算出传感器读数的分布，即均值和误差，用之前的表示方法如下式所示：
$\vec u_{expected}=H_k \hat x_k\\ \Sigma_{expected}=H_k P_k H^T_k$
卡尔曼滤波的一大优点就是能处理传感器噪声，换句话说，我们的传感器或多或少都有点不可靠，并且原始估计中的每个状态可以和一定范围内的传感器读数对应起来。从测量到的传感器数据中，我们大致能猜到系统当前处于什么状态。但是由于存在不确定性，某些状态可能比我们得到的读数更接近真实状态。我们将这种不确定性（例如：传感器噪声）用协方差 $R_K$表示，该分布的均值就是我们读取到的传感器数据，称之为 $\vec{z_k}$。
现在我们有了两个高斯分布，一个是在预测值附近，一个是在传感器读数附近。

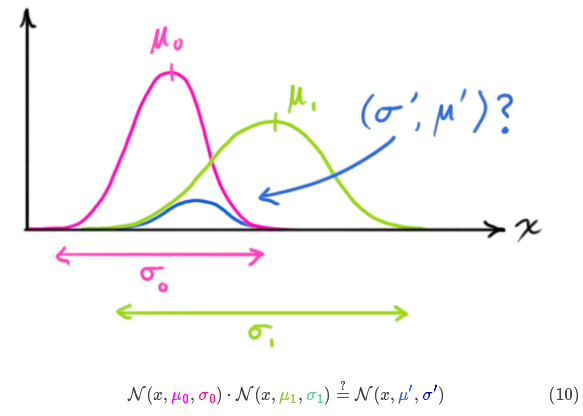
我们必须在预测值（粉红色）和传感器测量值（绿色）之间找到最优解。那么，我们最有可能的状态是什么呢？如果我们想知道这两种情况都可能发生的概率，将这两个高斯分布相乘就可以了。

融合高斯分布公式

先以一维高斯分布来分析，具有方差 $\sigma^2$ 和 $u$ 的高斯曲线可以用下式表示：

如果把两个服从高斯分布的函数相乘会得到什么呢？

将式（9）代入到式（10）中（注意重新归一化，使总概率为1）可以得到：

将式（11）中的两个式子相同的部分用 $K$ 表示：

下面进一步将式（12）和（13）写成矩阵的形式，如果 $\Sigma$ 表示高斯分布的协方差， $\vec u$ 表示每个维度的均值，则：

矩阵 $K$ 称为卡尔曼增益，下面将会用到。

将所有公式整合起来

我们有两个高斯分布，预测部分 $(u_0,\Sigma_0)=(H_k\hat{x_k},H_kP_kH^T_k)$ ，和测量部分 $(u_1,\Sigma_1)=(\vec{z_k},R_k)$，将它们放到式（15）中算出它们之间的重叠部分：

由式（14）可得卡尔曼增益为：

将式（16）和式（17）的两边同时左乘矩阵的逆（注意 $K$里面包含了 $H_k$ ）将其约掉，再将式（16）的第二个等式两边同时右乘矩阵 $H^T_k$ 的逆得到以下等式：

上式给出了完整的更新步骤方程。 $\hat{x_k}'$ 就是新的最优估计，我们可以将它和放 $P^{'}_k$到下一个预测和更新方程中不断迭代。

调整参数

卡尔曼滤波的核心代码虽然就短短的几行，但参数的确定却不是那么容易。在很多工业控制领域，比如飞船的控制、卫星的控制等都有专门的负责调参的工程师甚至是一个团队，可见卡尔曼滤波参数整定的重要程度。从某种意义上说，调参更像是一门艺术。针对于同一套工程模型，这些参数理论上应该可以统一，但是不同环境下系统的过程噪声以及测量噪声有可能不同，因此还是需要实际测试，以便于找到参数的最优值。可以参考这篇文章参数调整

其中大部分参数需要根据实际应用情况做调整，例如 $Q_k$值、 $R_k$值和 $P_k$的值，下面逐一进行介绍。 $Q_k$值为过程噪声，用来衡量预测模型计算的误差大小，如果其值越小系统对预测模型的信任度也就越高，系统也越发容易收敛，说明模型设计的较为合理。，具体的，如果 $Q_k$设置为零，说明系统非常相信预测模型不相信测量值，随着 $Q_k$值越来越大，系统对预测模型的信任度就越来越低，对测量值的信任度就越来越高，更甚者，如果 $Q_k$值无穷大，那么系统只信任测量值不相信预测值。 $R_k$值为测量噪声，代表着传感器测量误差，其值太小太大都不一定合适。如果 $R_k$太大，整个系统的响应时间就会变的比较慢，原因是系统对新的传感器测量的值不是那么相信，从而导致新来的值对整个系统影响不大。如果越小系统收敛越快，但如果 $R_k$越小，系统反应就越快，收敛速度也会越快，更甚者，如果 $R_k$过小就有可能导致系统出现震荡。 $R_k$的确定一般有如下两种方法，其一通过对传感器进行大量测试，记录出每个数据的输出，那么这些大量输出数据近似符合正态分布，根据 $3σ$原则，取该正态分布的 $(3σ)^2$作为 $R$的初始化值。其二可以查看说明书，传感器出厂时，厂家一般都会给出传感器测量误差值。最后一个关键参数是 $P_k$，它是状态向量 $\hat x_k$之间元素误差的协方差初始值，表示卡尔曼滤波系统对当前预测状态向量的置信度，其值越小说明系统就越相信当前预测状态。 $P_k$的大小决定了初始收敛速度。 $P_k$值的大小只是影响系统的初始收敛速度，在调试的时候，一般设一个较小的 $P_k$值，这样可以得到一个比较快的收敛速度，随着卡尔曼滤波的迭代， $P_k$的值会随着系统的迭代不断的改变，当系统进入到一个稳态的状态之后， $P_k$的值也会收敛成一个最小的协方差矩阵。对于 $Q_k$值和 $R_k$值，可以先将 $Q_k$值从小往大调整，将 $R_k$从大往小调整，这样系统可以较快的得到收敛，然后根据系统的收敛速度，固定一个值再去调整另外一个值。

代码例程（matlab）

代码例程（python）