同态加密BGV与BFV方案对比与梳理

Revisiting Homomorphic Encryption Schemes for Finite Fields

摘要

这篇文章主要回顾了BGV和BFV方案，展示其区别，并优化了BGV，BFV的RNS实现(BFV的加密，BFV乘法，BFV噪声管理，BFV解密)，并在PALISADE上面对其进行了效率测试。

在优化之前，同样的明文模数空间下，BGV的噪声增加要比BFV小，而优化之后，BFV比BGV稍好一点。

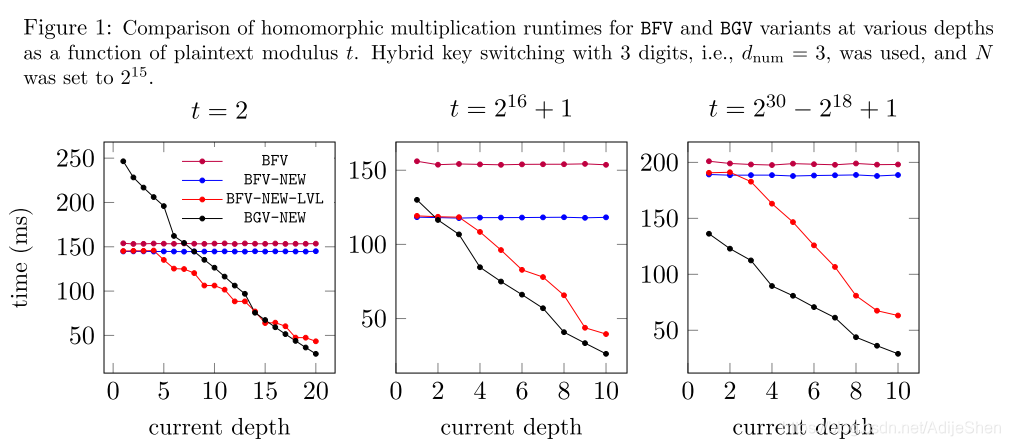
优化后的结果上来说，在明文空间模数较大或适中的情况下，BGV效率比较高，在模数比较小的情况下，BFV的效率高。

引言

BFV和BGV的明文空间都是 $Z_t$，模数为$Q$，

BGV方案将消息放在最小字节位(Least Significant Bit)上，使用模数替换技术来保持噪声为一个常量。具体来说，每次乘法之后都会将模数$Q$缩小一个噪声$B$的大小$Q/B$，而每次乘法后变为平方的噪声$B^2$也被缩小了一个噪声的大小变为$B$，因此噪声可以保持为一个常量。

BFV方案将消息放在最大字节位(Most Significant Bit)上，所有的密文在做乘法后都会缩小$Q/t$。模数$Q$保持不变，而噪声逐渐增加，噪声增加的量和BGV方案中$Q$缩小的量近似。

之前Costache和Smart做了一个噪声对比的测试，结果显示：在$t$较大时，BGV的噪声增加量要比BFV小。然而他们没有从理论上和实验上比较计算上的开销。

因此这篇文章主要贡献就是优化BGV和BFV方案，使得两者之间的差距缩小，并且从理论和实验上比较两者的效率差异。

修改BFV方案

作者提出了两个方法来改善BFV方案，第一种针对加密，第二种针对乘法操作

• 加密优化：BFV的密文可以表示为$\mathbf{c}=(\mathbf{b},\mathbf{a})$，其中$\mathbf{b}=\mathbf{a}\cdot \mathbf{s}+\mathbf{e}+\Delta \mathbf{m}$，$\Delta =\lfloor Q/t\rfloor$。BFV的主要开销就来自$Q/t$与$\lfloor Q/t\rfloor$之间的差距。
  令$r_t(Q)=Q-t\Delta$，只要令$r_t(Q)\approx 0$，那么就可以减少BFV的噪声增加，是的BFV的噪声近似于BGV，甚至比BGV更好。所以在修改中，令$\mathbf{b}=\mathbf{a}\cdot \mathbf{s}+\mathbf{e}+\lceil \frac{Q}{t}\mathbf{m}\rfloor$。
• 乘法优化：BFV的乘法时最耗时的步骤，因为它需要将两个密文${\mathbf{c}}_1$，${\mathbf{c}}_2$做相乘，然后再将乘积进行$t/Q$ scale。那这就需要将两个密文的模数$Q$扩展到$QP$，其中$P$是一个比$Q$足够大的数。做一次乘法就需要进行一次$QP$下的NTT，一次Scale down $Q/t$，最后将结果从模$P$中转到模$Q$中。本文作者提出了一个优化的乘法，能够做到$P\approx Q$，节省了模数扩张以及NTT的开销。
  主要的思想是对${\mathbf{c}}_2$进行模数替换，${\mathbf{c}}_2^{\prime }\mathrm{m}\mathrm{o}\mathrm{d}P\equiv {\mathbf{c}}_2\mathrm{m}\mathrm{o}\mathrm{d}Q$。对${\mathbf{c}}_1,{\mathbf{c}}_2^{\prime }$在乘法之后对其进行$t/P$ scale。那么进行完scale之后的密文就已经在$Q$内了，就无需进行从$P$到$Q$的rescale了。用一个${\mathbf{c}}_2$上的较小的rescale来代替乘积上的较大的rescale。

BFV优化方法

• Lazy rescale：在CKKS中，有一种lazy relinearization方法，在涉及对多个密文做相乘并聚合的时候，可以先做乘法，再做加法聚合，最后在聚合的密文上进行重线性化，可以减少重线性化的次数。同样的再BFV中可以做lazy rescale，延缓$t/Q$缩放的时间，对于乘法之后做加法的密文，先进行加法再进行rescale。
• RNS：对于BFV的RNS优化有两种方法，一种是Bajard-Eynard-Hasan-Zucca（BEHZ）^[5]算法，基于整数模算法以及Montgomery reduction算法。第二种是Halevi-Polyakov-Shoup（HPS）算法^[21]，基于整数模算法以及浮点数近似算法。HPS算法中的很大的一个制约在于他需要用到高精度（双精度/四精度）的浮点数，当CRT的模数取到47~58比特时候需要双精度的浮点数来近似了，更大的模数就需要四精度的浮点数了。
  于是他们就提出了一种 digit decomposition技术，来加入到HPS解密步骤中，只用双精度的浮点数来支持任意大小的CRT模数。
• 他们还应用了^[24]中提出的混合密钥转换(hybrid key switching)应用到了BFV RNS优化中。并说明了在乘法中需要用到的辅助的模数可以被混合密钥转换重利用。

BGV优化及可用性提升

这篇文章用了Gentry-Halevi-Smart(GHS)（HE-Lib）算法来作为实现BGV的基础。GHS虽然涉及一些RNS操作，但在key switching和部分modulus switching操作中仍然是用到了高精度的整数算法。但在这篇文章中，他们把所有高精度的整数都用了RNS来代替（采用了CRT decomposition技术），来达到了更好的效率。

效率比较结果

作者在PALISADE中做了BGV和BFV的实现，结果是：

• 之前BGV在大明文模数下噪声增长比较小，他们的结果是现在BFV和BGV在大明文模数下表现近似，稍好于BGV。

• BFV的效率在小明文模数下较好，BGV的效率在适中或者较大的模数情况下表现较好。

• 他们的BFV实现比之前最好的实现在深层（乘法）电路的评估上快了4倍。

背景知识

分圆多项式：$\mathcal{R}=\mathbb{Z}[X]/(X^N+1)$，${\mathcal{R}}_Q=\mathcal{R}/Q\mathcal{R}$。${\mathbb{Z}}_Q=(-Q/2,Q/2)\cap \mathbb{Z}$。

初始BGV方案

BGV方案主要涉及到一个modulus switching技术，可以将模$Q$的密文$ct$，转化为模$Q^{\prime }$的密文$c{t}^{\prime }$来保证噪声大小为常数。所以在BGV方案中，要执行$L$层的乘法电路，就要选取 $L+1$ 个模数$Q_0\left|Q_1\right|\dots \mid Q_L=Q$，$t$和$Q_L$互素。

公钥：$\mathrm{p}\mathrm{k}=\left([\mathbf{a}\cdot \mathbf{s}+t\mathbf{e}{]}_{Q_L},-\mathbf{a}\right)\in {\mathcal{R}}_{Q_L}^2$

加密：$\mathrm{c}\mathrm{t}=\left({\left[[\mathbf{m}{]}_t+\mathbf{u}\cdot \mathbf{p}{\mathbf{k}}_0+t{\mathbf{e}}_0\right]}_{Q_L},{\left[\mathbf{u}\cdot \mathbf{p}{\mathbf{k}}_1+t{\mathbf{e}}_1\right]}_{Q_L}\right)=\left({\mathbf{c}}_0,{\mathbf{c}}_1\right)$

可以简单点看作$\mathrm{c}\mathrm{t}\approx \left([\mathbf{m}{]}_t+\mathbf{a}\cdot \mathbf{s},-\mathbf{a}\right)$

解密：${\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}=[\mathbf{m}{]}_t+t\left(\mathbf{u}\cdot \mathbf{e}+{\mathbf{e}}_1\cdot \mathbf{s}+{\mathbf{e}}_0\right)=[\mathbf{m}{]}_t+t\mathbf{v}\mathrm{m}\mathrm{o}\mathrm{d}{Q}_L$

$m={\left[{\left[{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right]}_{Q_L}\right]}_t$

噪声要求$\Vert tv{\Vert }_{\infty }<Q/2\to \Vert v{\Vert }_{\infty }<\frac{Q}{2t}-\frac{1}{2}$

加法：${\mathbf{c}}_0+{\mathbf{c}}_0^{\prime }+\left({\mathbf{c}}_1+{\mathbf{c}}_1^{\prime }\right)\cdot \mathbf{s}={\left[\mathbf{m}+{\mathbf{m}}^{\prime }\right]}_t+t\left(\mathbf{v}+{\mathbf{v}}^{\prime }+\mathbf{u}\right)\mathrm{m}\mathrm{o}\mathrm{d}{Q}_i$

加密密文：${\mathrm{c}\mathrm{t}}_{\mathrm{a}\mathrm{d}\mathrm{d}}=\left({\left[{\mathbf{c}}_0+{\mathbf{c}}_0^{\prime }\right]}_{Q_i},{\left[{\mathbf{c}}_1+{\mathbf{c}}_1^{\prime }\right]}_{Q_i}\right)$

加法后噪声: $\Vert v{\Vert }_{\infty }+\Vert v^{\prime }{\Vert }_{\infty }+1$

乘法：$\left({\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right)\cdot \left({\mathbf{c}}_0^{\prime }+{\mathbf{c}}_1^{\prime }\cdot \mathbf{s}\right)={\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+t\left([\mathbf{m}{]}_t\cdot {\mathbf{v}}^{\prime }+\mathbf{v}\cdot {\left[{\mathbf{m}}^{\prime }\right]}_t+t\mathbf{v}\cdot {\mathbf{v}}^{\prime }+r_m\right)=[\mathbf{m}\cdot {\mathbf{m}}^{\prime }{]}_t+t{\mathbf{v}}_{mult}$

乘法密文：${\mathrm{c}\mathrm{t}}_{\mathrm{m}\mathrm{u}\mathrm{l}\mathrm{t}}=\left({\left[{\mathbf{c}}_0\cdot {\mathbf{c}}_0^{\prime }\right]}_{Q_i},{\left[{\mathbf{c}}_0\cdot {\mathbf{c}}_1^{\prime }+{\mathbf{c}}_1\cdot {\mathbf{c}}_0^{\prime }\right]}_{Q_i},{\left[{\mathbf{c}}_1\cdot {\mathbf{c}}_1^{\prime }\right]}_{Q_i}\right)\in {\mathcal{R}}_{Q_i}^3$

乘法后噪声变为：$\begin{array}{rl}{\Vert {\mathbf{v}}_{\text{mult }}\Vert }_{\infty }& ={\Vert [\mathbf{m}{]}_t\cdot {\mathbf{v}}^{\prime }+\mathbf{v}\cdot {\left[{\mathbf{m}}^{\prime }\right]}_t+t\mathbf{v}\cdot {\mathbf{v}}^{\prime }+{\mathbf{r}}_m\Vert }_{\infty }\\ & \le \frac{{\delta }_{\mathcal{R}}t}{2}\left(2\Vert \mathbf{v}{\Vert }_{\infty }{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+\Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+1\right)\end{array}$

模数替换(缩减)：

本文的定义如下：要将$Q_j$下的密文$ct$替换为$Q_i$下的密文$c{t}^{\prime }$。前提是$Q_i\equiv Q_j\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}t$

在BGV的论文中，是这样表述的：令$c{t}^{\prime }$为距离$(Q_i/Q_j)\cdot ct$最近的元素，使得$c{t}^{\prime }\equiv ct\mathrm{m}\mathrm{o}\mathrm{d}t$。

本文中的意思是一样的，但通过不同的方法表述出来：

$\mathbf{\delta }=\left(t{\left[-{\mathbf{c}}_0/t\right]}_{Q_j/Q_i},t{\left[-{\mathbf{c}}_1/t\right]}_{Q_j/Q_i}\right)\in {\mathcal{R}}^2$

${\mathrm{c}\mathrm{t}}^{\prime }=\frac{Q_i}{Q_j}\cdot \left({\mathbf{c}}_0+{\mathbf{\delta }}_0,{\mathbf{c}}_1+{\mathbf{\delta }}_1\right)\mathrm{m}\mathrm{o}\mathrm{d}{Q}_i$

GHS优化

因为在初始的BGV方案中，模数替换要求所有的$Q_i$满足$Q_i\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}t$，减少了模数的选取范围，所以在GHS中，通过直接加密$[Q_{L}m{]}_t$的形式，模数替换可以直接替换为$[Q_{i}m{]}_t$，而不需要满足$Q_i\equiv 1\mathrm{m}\mathrm{o}\mathrm{d}t$的条件。这样做的坏处就在于两个不同层之间的密文加法需要进行层同步后才可进行。

初始BFV方案

BFV方案其实是吧modulus switching的方法隐式的包含在了乘法中。

公钥：$\mathrm{p}\mathrm{k}=\left([\mathbf{a}\cdot \mathbf{s}+\mathbf{e}{]}_Q,-\mathbf{a}\right)\in {\mathcal{R}}_Q^2$

加密：$\text{ ct }=\left({\left[\Delta [\mathbf{m}{]}_t+\mathbf{u}\cdot \mathbf{p}{\mathbf{k}}_0+{\mathbf{e}}_0\right]}_Q,{\left[\mathbf{u}\cdot \mathbf{p}{\mathbf{k}}_1+{\mathbf{e}}_1\right]}_Q\right)$

可以看做：$\text{ ct }\approx \left(\Delta [\mathbf{m}{]}_t+\mathbf{a}\mathbf{s},-\mathbf{a}\right),\Delta =\lfloor Q/t\rfloor$

解密：${\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}=\Delta [\mathbf{m}{]}_t+\mathbf{u}\cdot \mathbf{e}+{\mathbf{e}}_1\cdot \mathbf{s}+{\mathbf{e}}_0=\Delta [\mathbf{m}{]}_t+{\mathbf{v}}_{\text{fresh }}\mathrm{m}\mathrm{o}\mathrm{d}Q$

${\mathbf{m}}^{\prime }=\lfloor \frac{t}{Q}{\left[{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right]}_Q]$

噪声要求：$\Vert v{\Vert }_{\infty }<\frac{Q}{2t}-\frac{r_t(Q)}{2}$

加法：${\mathbf{c}}_0+{\mathbf{c}}_0^{\prime }+\left({\mathbf{c}}_1+{\mathbf{c}}_1^{\prime }\right)\cdot \mathbf{s}=\Delta {\left[\mathbf{m}+{\mathbf{m}}^{\prime }\right]}_t+\mathbf{v}+{\mathbf{v}}^{\prime }-r_t(Q)\mathbf{u}\mathrm{m}\mathrm{o}\mathrm{d}Q$

加法密文：${\mathrm{c}\mathrm{t}}_{\mathrm{a}\mathrm{d}\mathrm{d}}=\left({\left[{\mathbf{c}}_0+{\mathbf{c}}_0^{\prime }\right]}_Q,{\left[{\mathbf{c}}_1+{\mathbf{c}}_1^{\prime }\right]}_Q\right)$

加法噪声：${\Vert {\mathbf{v}}_{\mathrm{a}\mathrm{d}\mathrm{d}}\Vert }_{\infty }={\Vert \mathbf{v}+{\mathbf{v}}^{\prime }+r_t(Q)\mathbf{u}\Vert }_{\infty }\le \Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+r_t(Q)$

乘法：$\begin{array}{rl}\left({\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right)\cdot \left({\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right)& =\left(\Delta [\mathbf{m}{]}_t+\mathbf{v}+Q\mathbf{k}\right)\cdot \left(\Delta {\left[{\mathbf{m}}^{\prime }\right]}_t+{\mathbf{v}}^{\prime }+Q{\mathbf{k}}^{\prime }\right)\\ & =\frac{Q}{t}\Delta {\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+\frac{Q}{t}{\mathbf{v}}_{\text{tensor }}+\frac{Q^2}{t}{\mathbf{k}}_{\text{tensor }}\end{array}$

乘法密文：${\mathrm{c}\mathrm{t}}_{\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{o}\mathrm{r}}=\left({\mathbf{c}}_0\cdot {\mathbf{c}}_0^{\prime },{\mathbf{c}}_0\cdot {\mathbf{c}}_1^{\prime }+{\mathbf{c}}_1\cdot {\mathbf{c}}_0^{\prime },{\mathbf{c}}_1\cdot {\mathbf{c}}_1^{\prime }\right)\in {\mathcal{R}}^3$

${\mathrm{c}\mathrm{t}}_{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}={\left[[\frac{t}{Q}{\mathrm{c}\mathrm{t}}_{\text{tensor }}\rfloor \right]}_Q\in {\mathcal{R}}_Q^3$

乘法噪声：$\frac{t}{Q}\left(c_{{\text{tensor }}_0}+c_{{\text{tensor }}_1}\cdot s+c_{{\text{tensor }}_2}\cdot s^2\right)=\Delta \left[m\cdot m^{\prime }\right]+v_{\text{tensor }}+Q{k}_{\text{tensor }}$

${\mathrm{c}\mathrm{t}}_{{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}_0}+{\mathrm{c}\mathrm{t}}_{{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}_1}\cdot \mathbf{s}+{\mathrm{c}\mathrm{t}}_{{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}_2}\cdot {\mathbf{s}}^2=\Delta \left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]+{\mathbf{v}}_{\text{tensor }}+{\mathbf{v}}_{\mathrm{r}}\mathrm{m}\mathrm{o}\mathrm{d}Q$

其中${\Vert {\mathbf{v}}_r\Vert }_{\infty }\le \left(1+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+{\delta }_{\mathcal{R}}^2{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}^2\right)/2$，${\mathbf{v}}_{\text{mult }}={\mathbf{v}}_{\text{tensor }}+{\mathbf{v}}_r$.

$\begin{array}{rl}{\Vert {\mathbf{v}}_{\mathrm{mult}}\Vert }_{\infty }\le & \frac{{\delta }_{\mathcal{R}}t}{2}(\frac{2\Vert \mathbf{v}{\Vert }_{\infty }{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }}{Q}+\left(4+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}\right)\left(\Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }\right)\\ & +r_t(Q)\left({\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+5\right))+\frac{1+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+{\delta }_{\mathcal{R}}^2{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}^2}{2}\end{array}$

RNS表示

中国剩余定理将${\mathbb{Z}}_Q$中的一个元素拆分为一组更小空间中的数（比如64位以内的数），来使得计算机可以快速的计算。这样的表示方法叫做剩余数系统(Residue-Number-System RNS)。

同样的，一个多项式环${\mathcal{R}}_Q$中元素也可以用他的剩余数来表示，具体来说，取一组互素的数$q_i$使得$Q=q_0\cdots q_L$，将多项式环的系数全都从${\mathbb{Z}}_Q$映射到${\mathbb{Z}}_{q_i}$中，然后进行NTT来做${\mathcal{R}}_Q$上元素的快速乘法操作。

在BGV方案中，通常取$Q_L=q_0\cdots q_L$，$Q_i=q_0\cdots q_i$，其中$q_i=1\mathrm{m}\mathrm{o}\mathrm{d}2N,1\le i\le L$。在BFV中，取$Q=q_0\cdots q_k$，$Q_i=q_0\cdots q_i$，其中$q_i=1\mathrm{m}\mathrm{o}\mathrm{d}2N,1\le i\le k$。这里用了两种不同的方法来对BGV和BFV的模数进行选取，是因为在BFV中，模数都是选取到软件/硬件能表达的最大位数(64/53)位。而在BGV方案中，模数的选取与每次需要减少的噪声大小有关，因此也与需要执行的算数电路有关。在HE-Lib中，有一个动态的噪声预估方法可以解除这种限制。因此，BGV的可用性是受到限制的。但在本文中，对BGV的噪声进行了统计地预估，增加了可用性。

在使用BFV方案乘法的时候，需要用到一个switchbase操作，就是将$\mathbf{a}\in {\mathcal{R}}_Q$的RNS表达转换为$[\mathbf{a}{]}_Q\mathrm{m}\mathrm{o}\mathrm{d}P$这样的形式。

按照原本中国剩余定理的表达，需要计算
$$\left(\sum _{i=1}^k(\mathbf{a}\mathrm{m}\mathrm{o}\mathrm{d}{q}_i)\left({\left(\frac{Q}{q_i}\right)}^{-1}\mathrm{m}\mathrm{o}\mathrm{d}{q}_i\right)\frac{Q}{q_i}\right)modQ$$
而在RNS表达中时存储的$[\mathbf{a}{]}_{q_i}$，所以一种快速的方法来计算的话是
$$\text{ FastBaseExtension }(\mathbf{a},Q,P)=\sum _{i=1}^k{\left[\mathbf{a}{\left(\frac{Q}{q_i}\right)}^{-1}\right]}_{q_i}\frac{Q}{q_i}\mathrm{m}\mathrm{o}\mathrm{d}{p}_j$$
但这样子得到的不是$[\mathbf{a}{]}_Q\mathrm{m}\mathrm{o}\mathrm{d}P$而是$[\mathbf{a}{]}_Q+\mathbf{u}Q\mathrm{m}\mathrm{o}\mathrm{d}P$.

于是需要通过^[21]中的floating-point instruction技术来得到$\mathbf{u}$：$\mathbf{u}=\lfloor {\sum }_{i=1}^k{\left[\mathbf{a}{\left(\frac{Q}{q_i}\right)}^{-1}\right]}_{q_i}\frac{1}{q_i}\rceil$或者蒙哥马利约化来去掉Q。

RNS混合密钥替换

密钥替换(key switching)将一个由${\mathbf{s}}_A$解密的密文$\mathrm{c}\mathrm{t}=\left({\mathbf{c}}_0,{\mathbf{c}}_1\right)\in {\mathcal{R}}_Q^2$转换为一个可以由$s_B$解密的密文${\mathrm{c}\mathrm{t}}^{\prime }=\left({\mathbf{c}}_0^{\prime },{\mathbf{c}}_1^{\prime }\right)\in {\mathcal{R}}_Q^2$，两者解密后得到的消息相同。

在BV^[9]中有一种进行key switching的方法，后来^[5]将其扩展到了RNS中，这种方法是将密文中的多项式环中元素进行digit decomposition。但是这种方法需要平方次的NTTs转换，且有很大的噪声。在GHS^[20]中，提出了一种噪声更小，只需要线性个NTT转换的方案，但这种方法需要将$N$翻倍或者将$Q$缩小2的次数。GHS还提出了一种混合方法，折中结合BV和GHS的方法来达到最好的效果。

优化BFV方案

注意到之前BGV和BFV的噪声对比中：

BGV：

加法：$\Vert {\mathbf{v}}_{add}{\Vert }_{\infty }=\Vert \mathbf{v}{\Vert }_{\infty }+\Vert {\mathbf{v}}^{\prime }{\Vert }_{\infty }+1$ ，

乘法：$\begin{array}{rl}{\Vert {\mathbf{v}}_{\text{mult }}\Vert }_{\infty }& ={\Vert [\mathbf{m}{]}_t\cdot {\mathbf{v}}^{\prime }+\mathbf{v}\cdot {\left[{\mathbf{m}}^{\prime }\right]}_t+t\mathbf{v}\cdot {\mathbf{v}}^{\prime }+{\mathbf{r}}_m\Vert }_{\infty }\\ & \le \frac{{\delta }_{\mathcal{R}}t}{2}\left(2\Vert \mathbf{v}{\Vert }_{\infty }{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+\Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+1\right)\end{array}$

BFV：

加法：${\Vert {\mathbf{v}}_{\text{add}}\Vert }_{\infty }\le \Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+r_t(Q)$

乘法：$\begin{array}{rl}{\Vert {\mathbf{v}}_{\mathrm{mult}}\Vert }_{\infty }\le & \frac{{\delta }_{\mathcal{R}}t}{2}(\frac{2\Vert \mathbf{v}{\Vert }_{\infty }{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }}{Q}+\left(4+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}\right)\left(\Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }\right)\\ & +r_t(Q)\left({\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+5\right))+\frac{1+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+{\delta }_{\mathcal{R}}^2{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}^2}{2}\end{array}$

BFV相比BGV的噪声项多了$r_t(Q)$这一项，也就造成了BFV的噪声增长会比BGV要快，这篇文章说明了$r_t(Q)$是完全可以避免的。

噪声减少

现在回顾一下BFV的乘法噪声，令两个要进行相乘的密文的噪声都是$V$，$B_{key}=1$，乘法的噪声就大约为：
$${\delta }_{\mathcal{R}}t\left(\left(5+{\delta }_{\mathcal{R}}\right)V+\frac{r_t(Q)}{2}\left({\delta }_{\mathcal{R}}+5\right)\right)+\frac{{\delta }_{\mathcal{R}}^2}{2}\approx {\delta }_{\mathcal{R}}^{2}t\left(V+\frac{r_t(Q)}{2}\right)$$
当乘法继续进行的时候$V$就比$r_t(Q)\approx t/2$要大很多，此时$r_t(Q)$带来的噪声影响不大。但考虑到第一次乘法，两个新加密的密文的噪声为${\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}=\Delta [\mathbf{m}{]}_t+\mathbf{u}\cdot \mathbf{e}+{\mathbf{e}}_1\cdot \mathbf{s}+{\mathbf{e}}_0=\Delta [\mathbf{m}{]}_t+{\mathbf{v}}_{\text{fresh }}\mathrm{m}\mathrm{o}\mathrm{d}Q$,$\Vert {\mathbf{v}}_{\text{fresh}}{\Vert }_{\infty }\le B_{\text{err }}\left(2{\delta }_{\mathcal{R}}{B}_{\text{key }}+1\right)\approx 2{\delta }_{\mathcal{R}}{B}_{\text{err }}$。根据同态加密标准，噪声分布都是${\sigma }_{\text{err}}=3.2$的高斯分布，$B_{\text{err}}=3.2\times 6$。${\delta }_R\le \sqrt{N}$，所以$V_{\text{init}}=2\times 6\times 3.2\times 2\sqrt{N}<77\sqrt{N}$，而$N$一般不超过$2^{16}$，因此初始噪声最多也就14比特左右。但如果取$t>2^{16}+1$，那么$r_t(Q)/2>2^{14}$就成了噪声的主要组成了。如果取$t=2^{60}$，那么初始噪声会比BGV要大44比特。

减小这个噪声项$r_t(Q)$的方法也很简单，如同BGV里面一样，取$q_i=1\mathrm{m}\mathrm{o}\mathrm{d}t$，那么$r_t(Q)=1$，但这样做会减少模数选取的范围，所以不做考虑，另一种方法是不断地选取$Q$直到$r_t(Q)<\sqrt{N}$，但其实有更加自然的方法。

在加密的时候，不选择使用$\Delta [\mathbf{m}{]}_t$，而是$\lfloor Q[\mathbf{m}{]}_t/t\rceil$的形式，那这样做的话，噪声就变了：
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \left[\frac{t}…
其中$\lfloor Q[m{]}_t/t\rceil =Q[m{]}_t/t+\mathbf{\epsilon }$. $\Vert \mathbf{\epsilon }{\Vert }_{\infty }\le 1/2$.

当$\frac{t}{Q}\Vert \mathbf{v}+\mathbf{\epsilon }{\Vert }_{\infty }<\frac{1}{2}$时解密正确，也就是$\Vert \mathbf{v}{\Vert }_{\infty }<\frac{Q}{2t}-\frac{1}{2}$，此时的解密噪声就和BGV一样了。

注意：这个形式的密文加密可以直接用RNS表示，因为
$$\lfloor \frac{Q[\mathbf{m}{]}_t}{t}\rceil =\frac{Q[\mathbf{m}{]}_t-[Q\mathbf{m}{]}_t}{t}=-\frac{[Q\mathbf{m}{]}_t}{t}\mathrm{m}\mathrm{o}\mathrm{d}Q$$

考虑一下修改后方案的加法噪声：
$$\begin{array}{rl}{\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}+{\mathbf{c}}_0^{\prime }+{\mathbf{c}}_1^{\prime }\cdot \mathbf{s}& =\frac{Q}{t}\left([\mathbf{m}{]}_t+{\left[{\mathbf{m}}^{\prime }\right]}_t\right)+\mathbf{v}+{\mathbf{v}}^{\prime }+\mathbf{\epsilon }+{\mathbf{\epsilon }}^{\prime }\\ & =\frac{Q}{t}\left({\left[\mathbf{m}+{\mathbf{m}}^{\prime }\right]}_t+t\mathbf{u}\right)+\mathbf{v}+{\mathbf{v}}^{\prime }+\mathbf{\epsilon }+{\mathbf{\epsilon }}^{\prime }\\ & =\frac{Q}{t}{\left[\mathbf{m}+{\mathbf{m}}^{\prime }\right]}_t+\mathbf{v}+{\mathbf{v}}^{\prime }+\mathbf{\epsilon }+{\mathbf{\epsilon }}^{\prime }\mathrm{m}\mathrm{o}\mathrm{d}Q\end{array}$$
此时加法噪声的bound为：

${\Vert {\mathbf{v}}_{\text{new-add}}\Vert }_{\infty }\le \Vert \mathbf{v}{\Vert }_{\infty }+{\Vert {\mathbf{v}}^{\prime }\Vert }_{\infty }+1$

加法噪声也和BGV一样了。

考虑乘法：

$\begin{array}{c}\left({\mathbf{c}}_0+{\mathbf{c}}_1\cdot \mathbf{s}\right)\cdot \left({\mathbf{c}}_0^{\prime }+{\mathbf{c}}_1^{\prime }\cdot \mathbf{s}\right)=\left(\frac{Q}{t}[\mathbf{m}{]}_t+\tilde{\mathbf{v}}+\mathbf{k}Q\right)\cdot \left(\frac{Q}{t}{\left[{\mathbf{m}}^{\prime }\right]}_t+{\tilde{\mathbf{v}}}^{\prime }+{\mathbf{k}}^{\prime }Q\right)\\ =\frac{Q^2}{t^2}{\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+\frac{Q}{t}{\mathbf{v}}_{\text{new-tensor }}+\frac{Q^2}{t}{\mathbf{k}}_{\text{new-tensor }}\\ {\mathbf{v}}_{\text{new-tensor }}=[\mathbf{m}{]}_t\cdot {\tilde{\mathbf{v}}}^{\prime }+{\left[{\mathbf{m}}^{\prime }\right]}_t\cdot \tilde{\mathbf{v}}+\frac{t}{Q}\tilde{\mathbf{v}}\cdot {\tilde{\mathbf{v}}}^{\prime }+t\left(\tilde{\mathbf{v}}\cdot {\mathbf{k}}^{\prime }+{\tilde{\mathbf{v}}}^{\prime }\cdot \mathbf{k}\right)\\ {\mathbf{k}}_{\text{new-tensor }}=[\mathbf{m}{]}_t\cdot {\mathbf{k}}^{\prime }+{\left[{\mathbf{m}}^{\prime }\right]}_t\cdot \mathbf{k}+t\mathbf{k}\cdot {\mathbf{k}}^{\prime }+{\mathbf{r}}_m\end{array}$

那么乘法噪声的bound就是：
$$\begin{array}{rl}{\Vert {\mathbf{v}}_{\text{new-mult }}\Vert }_{\infty }\le & \frac{{\delta }_{\mathcal{R}}t}{2}\left(\frac{2\Vert \tilde{\mathbf{v}}{\Vert }_{\infty }{\Vert {\tilde{\mathbf{v}}}^{\prime }\Vert }_{\infty }}{Q}+\left(4+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}\right)\left(\Vert \tilde{\mathbf{v}}{\Vert }_{\infty }+{\Vert {\tilde{\mathbf{v}}}^{\prime }\Vert }_{\infty }\right)\right)\\ & +\frac{1+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}+{\delta }_{\mathcal{R}}^2{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}^2}{2}\end{array}$$
后面可以证明这样的噪声和BGV里面的是近似的。

在GHS中有一种对于BGV的初始噪声减少手段对于BFV也是有用的，初始时选取一个比$Q$大的模数$Q_p=Q\cdot p$，然后加密完成直接执行scale down/modulus switching:${\text{ ct }}_{\text{scale }}=\lfloor \frac{1}{p}\text{ct}\rceil \mathrm{m}\mathrm{o}\mathrm{d}Q$

scale之后的噪声大小为${\Vert {\mathbf{v}}_{\mathbf{s}\mathbf{c}\mathbf{a}\mathbf{l}\mathbf{e}}\Vert }_{\infty }\le \frac{\Vert \mathbf{v}{\Vert }_{\infty }}{p}+\frac{1}{2p}+\frac{1+{\delta }_{\mathcal{R}}{B}_{\mathrm{k}\mathrm{e}\mathrm{y}}}{2}\approx \frac{{\delta }_R}{2}$。这样的大小要小于原始加密的噪声，可以作为一种降低初始噪声的手段。

改良乘法实现

缩小模数扩张$QP$:

在BGV里面，乘法可以直接在模$Q$中实现。然而在BFV中，乘法因为要进行scale down，不能进行取模，因此需要扩大模数。具体来说，取一个新的RNS模数$P=p_1\cdots p_{k^{\prime }}$使得$\text{ct}\cdot {\text{ct}}^{\prime }$不超过$PQ$的范围，所以在实践中，一般取$k^{\prime }=k+1$。来回顾一下原本BFV的乘法：
$$\begin{array}{l}\text{ Expand: ct }\in {\mathcal{R}}_Q^2\text{ and }{\mathrm{c}\mathrm{t}}^{\prime }\in {\mathcal{R}}_Q^2\to \mathrm{c}\mathrm{t}\in {\mathcal{R}}_{QP}^2\text{ and }{\mathrm{c}\mathrm{t}}^{\prime }\in {\mathcal{R}}_{QP}^2\\ ▹\mathrm{ct}(s)=\Delta [\mathbf{m}{]}_t+\mathbf{v}+Q\mathbf{k}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ ▹{\mathrm{c}\mathrm{t}}^{\prime }(\mathbf{s})=\Delta {\left[{\mathbf{m}}^{\prime }\right]}_t+{\mathbf{v}}^{\prime }+Q{\mathbf{k}}^{\prime }\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ {\text{ Tensor: ct }}_{\text{tensor }}=\left({\mathbf{c}}_0\cdot {\mathbf{c}}_0^{\prime },{\mathbf{c}}_0\cdot {\mathbf{c}}_1^{\prime }+{\mathbf{c}}_1\cdot {\mathbf{c}}_0^{\prime },{\mathbf{c}}_1\cdot {\mathbf{c}}_1^{\prime }\right)\in {\mathcal{R}}_{QP}^3:\\ ▹{\mathrm{c}\mathrm{t}}_{\text{tensor }}(\mathbf{s})=\frac{Q}{t}\Delta {\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+\frac{Q}{t}{\mathbf{v}}_{\text{tensor }}+\frac{Q^2}{t}{\mathbf{k}}_{\text{tensor }}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ \text{ ScaleDown: }{\mathrm{c}\mathrm{t}}_{\text{scale }}=\lfloor \frac{t}{Q}{\mathrm{c}\mathrm{t}}_{\text{tensor }}\rceil \in {\mathcal{R}}_P^3\\ ▹{\text{ ct }}_{\text{scale }}(s)=\Delta {\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+{\mathbf{v}}_{\text{tensor }}+Q{\mathbf{k}}_{\text{tensor }}+{\mathbf{v}}_r\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_P\right)\\ \text{ SwitchBasis: }{\mathrm{c}\mathrm{t}}_{\mathrm{s}\mathrm{c}\mathrm{a}\mathrm{l}\mathrm{e}}\in {\mathcal{R}}_P^3\to {\mathrm{c}\mathrm{t}}_{\text{scale }}\in {\mathcal{R}}_Q^3:\\ ▹{\text{ ct }}_{\text{scale }}(\mathbf{s})=\Delta {\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+{\mathbf{v}}_{\text{tensor }}+{\mathbf{v}}_r\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_Q\right)\end{array}$$
改良方法：对于$\mathrm{c}\mathrm{t}\in {\mathcal{R}}_Q^2,{\mathrm{c}\mathrm{t}}^{\prime }\in {\mathcal{R}}_Q^2$，对其中一个进行modulus switching，变为${\mathcal{R}}_P$中，通过一系列的分析，说明了$P\approx Q$就可以满足条件。看一下新的BFV乘法：
$$\begin{array}{rl}& \text{ ModSwitch: }\mathrm{c}\mathrm{t}\in {\mathcal{R}}_Q^2\to \widehat{\mathrm{c}\mathrm{t}}\in {\mathcal{R}}_P^2\\ & \text{ Expand: }\hat{\mathrm{c}}\mathrm{t}\in {\mathcal{R}}_P^2\to \widehat{\mathrm{c}\mathrm{t}}\in {\mathcal{R}}_{QP}^2\text{ and }{\mathrm{c}\mathrm{t}}^{\prime }\in {\mathcal{R}}_Q^2\to {\mathrm{c}\mathrm{t}}^{\prime }\in {\mathcal{R}}_{QP}^2\\ & ▹\widehat{\text{ct}}(s)=\frac{P}{t}[\mathbf{m}{]}_t+\frac{P}{Q}\tilde{\mathbf{v}}+P\mathbf{k}+{\epsilon }_{\text{round }}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ & ▹{\mathrm{ct}}^{\prime }(s)=\frac{Q}{t}{\left[{\mathbf{m}}^{\prime }\right]}_t+{\tilde{\mathbf{v}}}^{\prime }+Q{\mathbf{k}}^{\prime }\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ & \text{ Tensor: }{\widehat{\mathrm{c}\mathrm{t}}}_{\text{tensor }}=\left(\widehat{{\mathbf{c}}_0}\cdot {\mathbf{c}}_0^{\prime },\widehat{{\mathbf{c}}_0}\cdot {\mathbf{c}}_1^{\prime }+\widehat{{\mathbf{c}}_1}\cdot {\mathbf{c}}_0^{\prime },\widehat{{\mathbf{c}}_1}\cdot {\mathbf{c}}_1^{\prime }\right)\in {\mathcal{R}}_{QP}^3:\\ & ▹{\text{ ct }}_{\text{tensor }}(\mathbf{s})=\frac{QP}{t^2}{\left[\mathbf{m}\cdot {\mathbf{m}}^{\prime }\right]}_t+\frac{P}{t}{\hat{\mathbf{v}}}_{\text{tensor }}+\frac{QP}{t}{\hat{\mathbf{k}}}_{\text{tensor }}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{QP}\right)\\ & {\text{ ScaleDown: ct }}_{\text{scale }}=\lfloor \frac{t}{P}{\widehat{\mathrm{c}\mathrm{t}}}_{\text{tensor }}\rceil \in {\mathcal{R}}_Q^3\\ & ▹{\text{ct}}_{\text{scale}}(s)=\frac{Q}{t}{\left[m\cdot m^{\prime }\right]}_t+{\hat{v}}_{\text{tensor}}+v_r\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_Q\right)\end{array}$$
考虑一下做basis extension的次数：在初始的BFV乘法中，Expand中有4步，ScaleDown中有3步，SwitchBasis中有3步，一共10步。而在新的BFV乘法中，ModSwitch中有2步，Expand中有4步，ScaleDown中有3步。一共有9步。因此，新的BFV乘法不仅P取的比之前小了，而且执行basis extension的次数也比初始的BFV方案要少一点。

分层BFV乘法：

和BGV一样，BFV中也可以使用分层的思想，令模数为$Q_{\ell }=q_1\cdots q_{\ell }$，并且在计算过程中执行modulus switching。但是，这样做的话那也就涉及到了不同层之间密文的处理以及噪声的管理。

为了维持BFV的可用性，他们提出了一种预放缩的方法，先将密文缩放$\frac{Q_{\ell }}{Q}$，对缩放后的密文进行乘法，然后将结果再乘以$\frac{Q}{Q_{\ell }}$回到$\mathrm{m}\mathrm{o}\mathrm{d}Q$下，

中间过程中经过模数转换的密文噪声为：$\hat{\mathbf{v}}=\frac{Q_{\ell }}{Q}\mathbf{v}+{\epsilon }_{\text{round }}$，其中${\epsilon }_{\text{round}}$的大小大约为$\frac{{\delta }_{\mathcal{R}}}{2}$。为了使噪声和缩放前保持基本一致，要求$\frac{Q_{\ell }}{Q}\Vert \mathbf{v}{\Vert }_{\infty }\gg \Vert {\epsilon }_{\text{round}}{\Vert }_{\infty }$ $\to$ $\Vert \mathbf{v}{\Vert }_{\infty }\gg \frac{Q{\delta }_{\mathcal{R}}}{2Q_{\ell }}\text{ and }\Vert \mathbf{v}{\Vert }_{\infty }^{\prime }\gg \frac{Q{\delta }_{\mathcal{R}}}{2Q_{\ell }}$。在实现中，往往取$\Vert \mathbf{v}{\Vert }_{\infty }>8\frac{Q{\delta }_{\mathcal{R}}}{Q_{\ell }}\text{ and }\Vert \mathbf{v}{\Vert }_{\infty }^{\prime }>8\frac{Q{\delta }_{\mathcal{R}}}{Q_{\ell }}$。

新的BFV乘法过程如下：
$$\begin{array}{rl}& \text{ ModSwitchDown: }\widehat{\mathrm{c}\mathrm{t}}=\lfloor \frac{Q_{\ell }}{Q}\mathrm{c}\mathrm{t}\rceil \in {\mathcal{R}}_{Q_{\ell }}^2\text{ and }c{\hat{\mathrm{t}}}^{\prime }=\lfloor \frac{Q_{\ell }}{Q}{\mathrm{c}\mathrm{t}}^{\prime }\rceil \in {\mathcal{R}}_{Q\ell }^2\\ & ▹\hat{\mathbf{v}}=\frac{Q_{\ell }}{Q}\mathbf{v}+{\epsilon }_{\text{round }}\text{ and }▹{\hat{\mathbf{v}}}^{\prime }=\frac{Q_{\ell }}{Q}{\mathbf{v}}^{\prime }+{\epsilon }_{\text{round }}^{\prime }\\ & {\hat{\mathrm{t}}}_{\mathrm{m}}=\mathrm{New}\mathrm{M}\mathrm{u}\mathrm{l}t\left(\widehat{\mathrm{c}\mathrm{t}},{\widehat{\mathrm{c}\mathrm{t}}}^{\prime }\right)\in {\mathcal{R}}_{Q_{\ell }}^3\\ & ▹{\widehat{\mathrm{c}\mathrm{t}}}_{\mathrm{m}}(\mathbf{s})=\frac{Q_{\ell }}{t}{\left[{\mathbf{m}}_1{\mathbf{m}}_2\right]}_t+{\hat{\mathbf{v}}}_{\mathrm{m}}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{Q_{\ell }}\right)\\ & \text{ ModSwitchUp: }{\mathrm{c}\mathrm{t}}_{\mathrm{m}}=\lfloor \frac{Q}{Q_{\ell }}{\hat{\mathrm{t}}}_{\mathrm{m}}\rceil \in {\mathcal{R}}_Q^3\\ & ▹{\mathrm{ct}}_{\mathrm{m}}(\mathbf{s})=\frac{Q}{t}{\left[{\mathbf{m}}_1{\mathbf{m}}_2\right]}_t+{\mathbf{v}}_{\mathrm{m}}\left(\mathrm{m}\mathrm{o}\mathrm{d}{\mathcal{R}}_{Q_{\ell }}\right)\\ & ▹{\mathbf{v}}_{\mathrm{m}}=\frac{Q}{Q_{\ell }}{\hat{\mathbf{v}}}_{\mathrm{m}}+{\mathbf{v}}_r\end{array}$$

优化HPS RNS variant解密

看不懂，待补充。

更加实用的BGV方案

静态噪声处理（通过模数选取的方式）

BGV在使用过程中，需要精确地预估出目前的噪声大小，然后动态地决定什么时候进行模数缩减，每次的缩放系数是多少。在HE-Lib中有详实的噪声动态分析技术。因为BFV是采用了最大位编码，缩放系数$Q/t$比较大，对噪声不是那么敏感，只要确定一个噪声的上界就可以了，而BGV时最小位编码，而且每次的缩放系数较小，所以需要更加准确的噪声控制。

在这篇文章的实现中，他们不进行动态的噪声控制，而是提前输入一些参数：乘法深度，每个乘法层中加法的最大次数，第一次乘法之前的加法和旋转次数。然后就可以生成所有的模数$Q_L,Q_{L-1},...,Q_1,Q_0$，更具这些模数来进行模数缩减就可以保证噪声控制在一个较小的范围内。在每次乘法前会自动执行模数缩减，这样子修改那么BGV的可用性就和BFV差不多了。

然后这篇文章就计算了具体的每个模数如何选取，最后得出结论：
$$\begin{array}{c}{q}_0>2t{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }-t\\ q_i>2\left(\left(n_{\mathrm{a}\mathrm{d}\mathrm{d}}^{\prime }+1\right)\frac{{\delta }_{\mathcal{R}}t}{2}\left(2{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }+2+\frac{1}{{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }}\right)+\left(n_{\mathrm{k}\mathrm{s}}^{\prime }+1\right)\frac{{\Vert {\mathbf{v}}_{\mathrm{k}\mathrm{s}}\Vert }_{\infty }}{{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }}\right)\\ q_{L+1}>2\left(\left(n_{\mathrm{a}\mathrm{d}\mathrm{d}}+1\right)\frac{{\Vert {\mathbf{v}}_{\mathrm{f}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{h}}\Vert }_{\infty }}{{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }}+n_{\mathrm{k}\mathrm{s}}\frac{{\Vert {\mathbf{v}}_{\mathrm{k}\mathrm{s}}\Vert }_{\infty }}{{\Vert {\mathbf{v}}_{\mathrm{c}}\Vert }_{\infty }}\right)\end{array}$$
其中$Q_0=q_0,Q_i=Q_{i-1}{q}_i$，$Q_{L+1}=Q_L{q}_{L+1}$，$Q_{L+1}$是最初密文加密用的模数，然后会直接进行一次模数缩减到$Q_L$中来降低初始噪声，所以总共的层数是$L$层。

处理不同层的密文之间的操作

在HE-Lib中，每个密文都有不同的缩放系数，导致需要将两个密文通过好几次scalar product来统一缩放系数，而在本文的实现中，每一层的缩放系数是一样的，那么就减少了scalar product的次数。

BFV和BGV比较

以下比较是本文优化过的BFV与BGV的比较，并不是原本方案的比较。

噪声增长

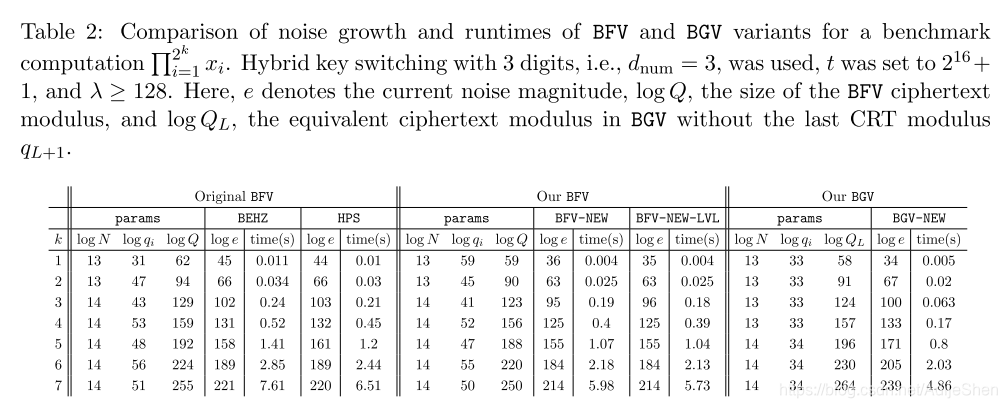
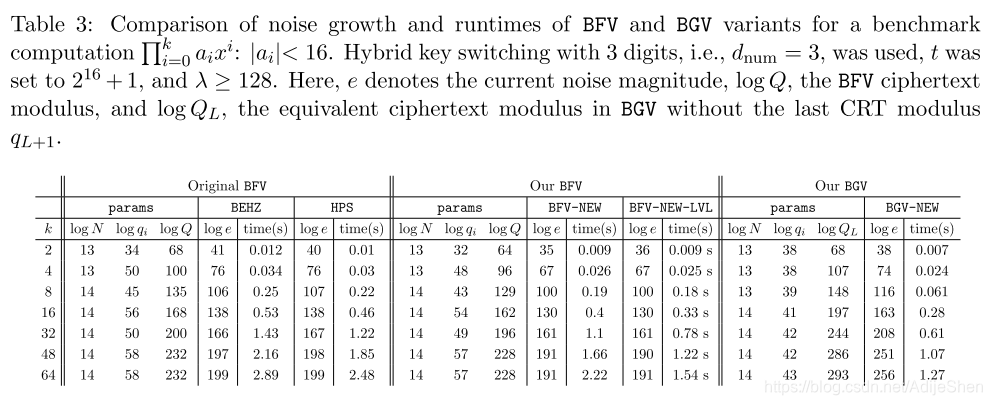
分析过程不看，结论上来说，BGV和BFV在$Q_0$时的噪声一致。在其余每一个乘法层中，BFV的每一层乘法噪声比BGV小1比特。而对于密钥替换（重线性化）操作来说，在明文模数较小的情况下 ($t\ll 2^{16}+1$)，BFV会有优势，在明文模数变大的情况下，BGV会有优势。总体来说，BFV和BGV的噪声增长系数类似，优化过的BFV可能会比BGV有稍微有一点点点点优势。具体可以看实验结果内的数据。

计算复杂度

BFV和BGV最大的计算区别在于乘法之后的scale down，BFV中因为采用了MSD编码，每次乘法完都需要scale down一个很大的$Q/t$，而对于BGV来说，只需要scale down一个和初始噪声差不多大小的模数，因此很容易想象BGV的效率是远远高于BFV的。统计下来，BFV的乘法，scaledown，重线性化总计需要$16\ell +\alpha \left(d_{\text{num}}^2+3\right)$个NTT，BGV的乘法，重线性化，modulus switching总计需要$7{\ell }^{\prime }+4+\alpha \left(d_{\text{num}}^2+2\right)$个NTT。看上去BFV需要NTT的数量是BGV的2x左右，但是实际上因为模数选取的关系，BFV中$q_i$都会取得尽可能大(60bit)，而在t=2的时候，BGV的$q_i$只需要取到20bit$(t\cdot {\delta }_R^2)$左右，因此${\ell }^{\prime }>3\ell$，此时BFV使用NTT数量要小于BGV；但是当$t=2^{16}+1$时，${\ell }^{\prime }\approx 2\ell$，此时BGV效率略优于BFV，当$t$再取大一点的时候，BGV的噪声就比BFV要高很多了。

实验结果