给定一个非负整数数组,a1, a2, …, an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
示例:
输入:nums: [1, 1, 1, 1, 1], S: 3
输出:5
解释:
-1+1+1+1+1 = 3
+1-1+1+1+1 = 3
+1+1-1+1+1 = 3
+1+1+1-1+1 = 3
+1+1+1+1-1 = 3
一共有5种方法让最终目标和为3。
分析:
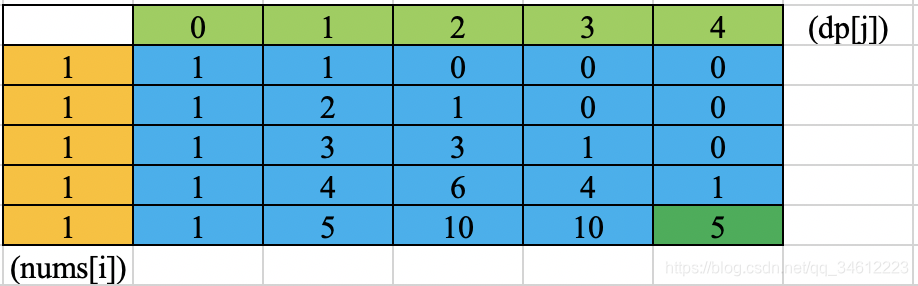
动态规划,将问题转化为0-1背包问题,将目标S转换成背包中不同体积的物品装法问题,递推公式为 d[j] = d[j] + d[j - nums[i]],遍历从后向前,保证每个物品(nums[j])只使用一遍,以{1,1,1,1,1}为例,画出状态转移表如下图
public:
int findTargetSumWays(vector<int>& nums, int S) {
int wayTimes = 0;
int sum = 0;
for(int i = 0; i < nums.size(); i++) sum += nums[i];
if (S > sum) return 0; // sum全为正数组成也无法找到S
// 我们假设P是正子集,N是负子集
// 例如: 假设nums = [1, 2, 3, 4, 5],target = 3,
// 一个可能的解决方案是+1-2+3-4+5 = 3 这里正子集P = [1, 3, 5]和负子集N = [2, 4]
// 满足 x - (sum - x) = S => x = (S + sum) / 2
// 推导: 假设加法的总和为x,那么减法对应的总和就是sum - x
if ((S + sum) % 2 == 1) return 0;
int bagSize = (S + sum) / 2;
vector<int> dp(bagSize + 1, 0);
dp[0] = 1;
for(int i = 0; i < nums.size(); i++){
for(int j = bagSize; j >= nums[i]; j--){
dp[j] += dp[j - nums[i]];
}
}
for(int x : dp) cout << x <<" ";
return dp[bagSize];
}
