一、最小二乘法
对于给定的数据集\(D = {(x_1,y_1),(x_2,y_2), ...,(x_m,y_m)}\),其中\(x_i=(x_{i1};x_{i2}; ...;x_{id})\)。
对上述数据进行拟合:
\[f(x_i)= \hat \omega^T \hat{x_i} \]
其中:\(\hat\omega = (\omega_1;\omega_2; ..., \omega_d;b)\) , \(\hat x_i = (x_{i1};x_{i2}; ...;x_{id};1)\)
最小二乘法是使用均方误差函数进行度量,可以通过求导,令导数等于零,直接求出解析解。均方误差函数为:
\[E(\hat \omega)=\frac{1}{m}\sum_{i=1}^m(f(x_i)-y_i)^2 \]
\(X=(x_1^T;x_2^T; ...;x_m^T), Y=(y_1;y_2;...;y_m)\),则:
\[E(\hat \omega)=(X*\hat\omega)^T(X*\hat\omega) \]
上式对\(\omega\)求导,得:
\[\frac{\partial E}{\partial\hat\omega}=\frac{2}{m}X^T(X\hat\omega-Y) \]
令上述导数等于0,得:
\[\hat\omega^*=(X^TX)^{-1}X^TY \]
这就是要求的最优解
使用上述方法,随机生成三维数据集,使用最小二乘法进行线性回归
clc;
M = 50;
dim = 2;
X = 10*randn(M,dim);
Y = 10*rand(M,1);
figure(1);
scatter3(X(:,1),X(:,2),Y,'filled');
X_2 = ones(M,1);
X = [X,X_2];
omega = (X'*X)\X'*Y;
[xx,yy] = meshgrid(-20:0.2:20,-20:0.2:20);
zz = omega(1,1)*xx+omega(2,1)*yy+omega(3,1);
hold on;
surf(xx,yy,zz);
效果
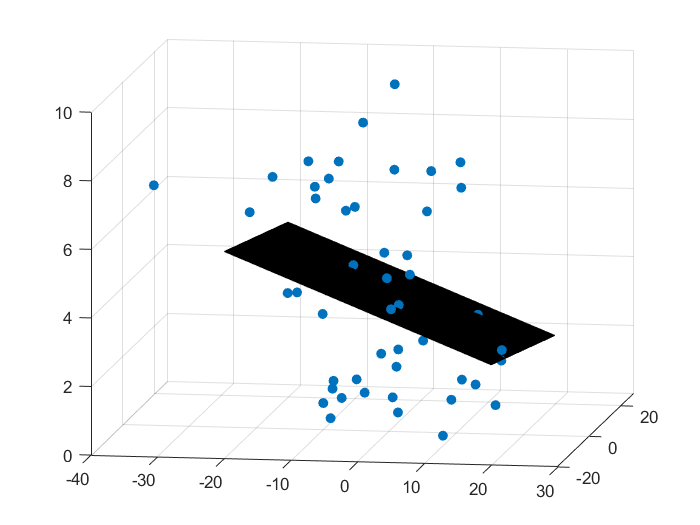
二、梯度下降法
相较于均方误差函数,对\(\omega_j , j = 1, ..., d\)求导得:
\[\frac{\partial f}{\partial \omega_j}=\frac{2}{m}\sum_{i=1}^m x_{ij}(x_{ij}\omega_j-y_i) \]
使用matlab生成三维随机数,检验程序有效性
clc;
close all;
M = 50; %%50个样本
dim = 2;
N = dim+1;
X = 10*randn(M,dim);
Y = 10*rand(M,1);
figure(1);
scatter3(X(:,1),X(:,2),Y,'filled');
X_2 = ones(M,1);
X = [X,X_2];
iterate = 300; %%迭代300次
count = 0;
omega = zeros(dim+1,1);
err = 1000;
delta_t = 0.01;
loss_data = zeros(1,iterate);
while count <= iterate && err > 0.1
count = count+1;
delta_omega = zeros(N,1);
for i = 1:N
temp_omega = 0;
for j = 1:M
temp_omega = temp_omega+X(j,i)*(X(j,i)*omega(i,1)-Y(j,1));
end
delta_omega(i,1) = temp_omega/M;
end
omega = omega - delta_t*delta_omega;
disp(omega);
err = (Y-X*omega)'*(Y-X*omega);
disp(err);
loss_data(1,count) = err;
end
[xx,yy] = meshgrid(-20:0.2:20,-20:0.2:20);
%
zz = omega(1,1)*xx+omega(2,1)*yy+omega(3,1);
hold on;
surf(xx,yy,zz);
figure(2);
x_t = linspace(0,iterate,size(loss_data,2));
plot(x_t,loss_data);
效果
样本和分类面
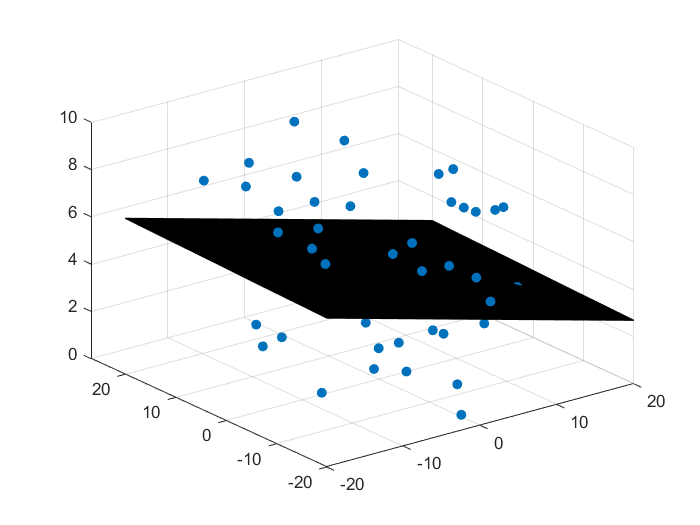
损失函数随迭代次数变化

conclusion
1、对于\(\Delta \omega\),注意是军方误差,如果不除以数据集元素个数,所得梯度向量的模可能过大,程序不能收敛