线性回归
回归分析(regression analysis)用来建立方程模拟两 个或者多个变量之间如何关联
被预测的变量叫做:因变量(dependent variable), 输出(output)
被用来进行预测的变量叫做: 自变量(independent variable), 输入(input)
一元线性回归包含一个自变量和一个因变量
以上两个变量的关系用一条直线来模拟
如果包含两个以上的自变量,则称作多元回归分析 (multiple regression)
线性回归假定输入变量(X)和单个输出变量(Y)之间呈线性关系。它旨在找到预测值 Y 的线性方程:y = ax + b
代价函数
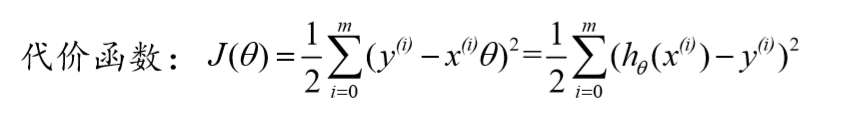
则对于每个样本点 ,根据我们的直线方程,预测值为: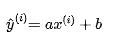
很显然,我们希望直线方程能够尽可能地拟合真实情况,也就是说真值 和预测值 的差距尽量小。只有所有的样本的误差都小,才能证明我们找出的直线方程拟合性好。
通常来说,为了防止正误差值和负误差值相抵的情况,使用绝对值来表示距离:
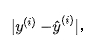
但是在线性回归中,我们需要找极值,需要函数可导,而 不是一个处处可导的函数,因此很自然地想到可以使用:
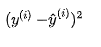
故损失函数采用的平方值
线性回归中经常使用的两种算法
最小二乘法:
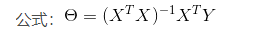
公式推到:见博文:
https://blog.csdn.net/qq_27576655/article/details/82218489
最小二乘法存在的问题:
1.X矩阵必须是可逆的
2.当特征较多时,求逆运算时间开销较大
梯度下降法
利用迭代的思想,不断的更新θ值,最终θ会收缩到某个值上。
θ的变化公式:
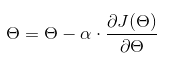
α为步长,学习率
例如 线性模型为:
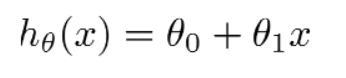
代价函数为:
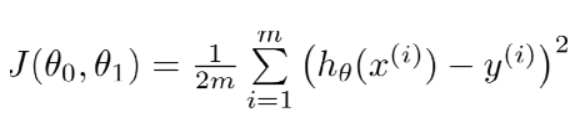
我们所求的最终结果是这样
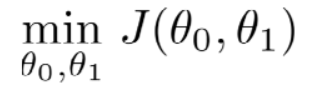
首先初始化θ0、θ1
不断改变θ0、θ1的值,直到J(θ0、θ1)到达一个全局最小值或局部极小值
梯度下降法不同于最小二乘法,最小二乘法求的是全局最小值,而梯度下降法可能是全局最小值,也可能是局部极小值,梯度下降法每一次下降的方向已经是确定的,但学习率需要我们去设定,不宜大,也不宜太小,太大达不到局部极小值,太小迭代速度慢,多尝试一些值,比如0.1、0.03等等
如何解决线性回归中的过拟合现象
过拟合产生的原因是因为θ值过多或者是θ值过哦大造成的,解决方法可以使用L1正则(又称为lasso回归)或者L2正则(又称为ridge回归,岭回归)或者elastic net(弹性网络)算法
L1正则公式如下,其中 λ>0
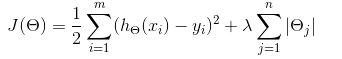
L2正则公式如下:其中 λ>0
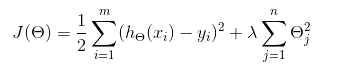
elastic net公式如下:其中 λ>0,p在[0,1]之间
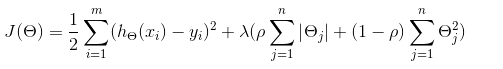
特点:Ridge模型具有较高的准确性、鲁棒性以及稳定性,不会丢失特征;LASSO模型具有较高的求解
速度(会丢失特征);elastic net 综合两者的优点
机器学习调参
在实际工作中,对于各种算法模型(线性回归)来讲,我们需要获取θ、λ、p的值;θ的求解其实就是算法模型的求解,一般不需要开发人员参与(算法已经实现),主要需要求解的是λ和p的值,这个过程就叫做调参(超参)
交叉验证:将训练数据分为多份,其中一份进行数据验证并获取最优的超参:λ和p;比如:十折交叉验证、五折交叉验证(scikit-learn中默认)等
期望风险、经验风险与结构风险之间的关系
首先了解一下损失函数有哪些
损失函数是衡量预测模型预测期望结果表现的指标。损失函数越小,模型的鲁棒性越好。。
常用损失函数有:
1.0-1损失函数:用来表述分类问题,当预测分类错误时,损失函数值为1,正确为0
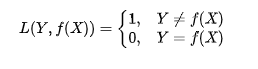
2.平方损失函数:用来描述回归问题,用来表示连续性变量,为预测值与真实值差值的平方。(误差值越大、惩罚力度越强,也就是对差值敏感)
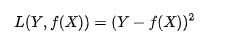
3.绝对损失函数:用在回归模型,用距离的绝对值来衡量

4.对数损失函数:是预测值Y和条件概率之间的衡量。事实上,该损失函数用到了极大似然估计的思想。P(Y|X)通俗的解释就是:在当前模型的基础上,对于样本X,其预测值为Y,也就是预测正确的概率。由于概率之间的同时满足需要使用乘法,为了将其转化为加法,我们将其取对数。最后由于是损失函数,所以预测正确的概率越高,其损失值应该是越小,因此再加个负号取个反。
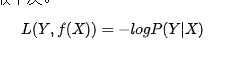
我们已经清楚了,对于具体的某个样本点,有了衡量其预测值与真实值的差异度的方法了(选取上面任意一个损失函数即可)。
通过损失函数我们只能知道模型决策函数f(X)对于单个样本点的预测能力(借用损失函数L(Y,f(x)),损失函数越小,说明模型对于该样本预测越准确。),那么如果想知道模型f(X)对训练样本中所有的样本的预测能力应该怎么办呢?显然只需所有的样本点都求一次损失函数然后进行累加就好了。如下式
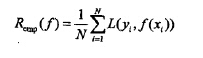
这就经验风险,所谓的经验风险最小化便是让这个式子最小化,注意这个式子中累加和的上标N表示的是训练样例集中样本的数目。
经验风险是对训练集中的所有样本点损失函数的平均最小化。经验风险越小说明模型f(X)对训练集的拟合程度越好,但是对于未知的样本效果怎么样呢?我们知道未知的样本数据(<X,Y>)的数量是不容易确定的,所以就没有办法用所有样本损失函数的平均值的最小化这个方法,那么怎么来衡量这个模型对所有的样本(包含未知的样本和已知的训练样本)预测能力呢?熟悉概率论的很容易就想到了用期望。即假设X和Y服从联合分布P(X,Y).那么期望风险就可以表示为:
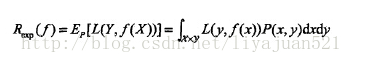
这就是期望风险,期望风险表示的是全局的概念,表示的是决策函数对所有的样本<X,Y>预测能力的大小,而经验风险则是局部的概念,仅仅表示决策函数对训练数据集里样本的预测能力。理想的模型(决策)函数应该是让所有的样本的损失函数最小的(也即期望风险最小化),但是期望风险函数往往是不可得到的,即上式中,X与Y的联合分布函数不容易得到。现在我们已经清楚了期望风险是全局的,理想情况下应该是让期望风险最小化,但是呢,期望风险函数又不是那么容易得到的。怎么办呢?那就用局部最优的代替全局最优这个思想吧。这就是经验风险最小化的理论基础。
经验风险是局部的,基于训练集所有样本点损失函数最小化的。
期望风险是全局的,是基于所有样本点的损失函数最小化的。
经验风险函数是现实的,可求的;
期望风险函数是理想化的,不可求的;
只考虑经验风险的话,会出现过拟合的现象,过拟合的极端情况便是模型f(x)对训练集中所有的样本点都有最好的预测能力,但是对于非训练集中的样本数据,模型的预测能力非常不好。怎么办呢?这个时候就引出了结构风险。结构风险是对经验风险和期望风险的折中。在经验风险函数后面加一个正则化项(惩罚项)便是结构风险了。如下式:
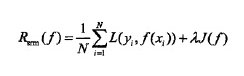
相比于经验风险,结构风险多了一个惩罚项,其中是一个lamada是一个大于0的系数。J(f)表示的是是模型f的复杂度。结构风险可以这么理解:
经验风险越小,模型决策函数越复杂,其包含的参数越多,当经验风险函数小到一定程度就出现了过拟合现象。也可以理解为模型决策函数的复杂程度是过拟合的必要条件,那么我们要想防止过拟合现象的方式,就要破坏这个必要条件,即降低决策函数的复杂度。也即,让惩罚项J(f)最小化,现在出现两个需要最小化的函数了。我们需要同时保证经验风险函数和模型决策函数的复杂度都达到最小化,一个简单的办法把两个式子融合成一个式子得到结构风险函数然后对这个结构风险函数进行最小化。
线性回归算法假设:
1、随机误差项是一个期望值或平均值为0的随机变量;
2、对于解释变量的所有观测值,随机误差项有相同的方差;
3、随机误差项彼此不相关;
4、解释变量是确定性变量,不是随机变量,与随机误差项彼此之间相互独立;
5、解释变量之间不存在精确的(完全的)线性关系,即解释变量的样本观测值矩阵是满秩矩阵;
6、随机误差项服从正态分布。
