Compartilhador: Wu Shaojun ｜Escola**: Universidade de Ciência Eletrônica e Tecnologia da China**
breve introdução
Superar o crescimento exponencial da complexidade ao simular sistemas quânticos de muitos corpos é um objetivo desafiador na física. Atualmente, para as propriedades do estado fundamental de sistemas quânticos unidimensionais, métodos baseados em estados de rede tensorial (TNS) forneceram uma maneira eficaz de fornecer soluções numéricas basicamente precisas. Em sistemas bidimensionais, também foi feito algum progresso com a introdução de alguns algoritmos para otimizar o TNS para vários modelos de rede. Desta vez, apresentaremos um novo método de representação de estado quântico, nomeadamente TNS isométrico, que pode ser usado para descrever o estado quântico de um sistema bidimensional e tem vantagens computacionais. reconstruir o estado quântico Um método para construir MPS, que possui apenas um número linear de operações.
Artigos relacionados 1
**Título: Estados de rede de tensores isométricos em duas dimensões
Autor: Michael P. Zaletel e Frank Pollmann
Journal: **Phys Rev.
**Data de publicação:** 24 de janeiro de 2020
Artigos Relacionados 2
**Crédito: Tomografia de estado quântico eficiente
Créditos: Marcus Cramer, Martin B. Plenio, Steven T. Flammia, Rolando Somma, David Gross, Stephen D. Bartlett, Olivier Landon-Cardinal, David Poulin e Yi-Kai Liu
:** Natureza Comunicações 1, 149(2010)
**Publicado:** 21 de dezembro de 2010
01
** introdução
**
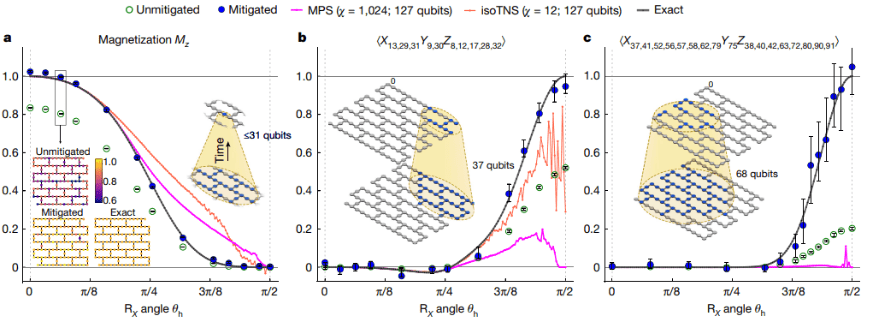
(Fonte da imagem: Nature volume 618, páginas 500–505 (2023))
Recentemente, a IBM implementou a simulação do modelo Ising de campo transversal bidimensional em 127 processadores quânticos. Para comparação, simulações clássicas precisam ser usadas para obter resultados precisos. Este trabalho usa observações de peso 1, peso 10 e peso 17 para medir o circuito quântico do trotador de 5 passos, e os resultados experimentais são mostrados na figura.
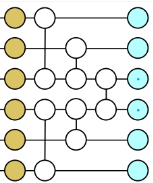
Ao realizar simulações clássicas para obter soluções precisas, o método de cone de luz e profundidade reduzida (LCDR) é usado aqui. Está dividido em duas partes. Uma parte é reduzir o número de camadas do circuito que precisam ser simuladas através das características entre portas quânticas e a outra parte é considerar que os qubits relacionados à quantidade de observação A são locais, o que significa que; apenas uma parte dos qubits precisa ser considerada. O Evolution pode então calcular o resultado da observação final em vez de todos os 127 bits. Os números de qubit relacionados das observações de peso 1, peso 10 e peso 17 são 31, 37 e 68, respectivamente. É importante notar que a simulação com 68 qubits ainda está além das capacidades das simulações de força bruta dos computadores clássicos. Portanto, este trabalho introduz redes de tensores, estados de produtos de matrizes 1D (MPS) e estados de redes de tensores isométricos 2D (iso TNS), para simulação.
02
** Introdução ao estado do produto matricial (MPS)
**
1. Conhecimento básico de tensores
(1) Definição e representação gráfica
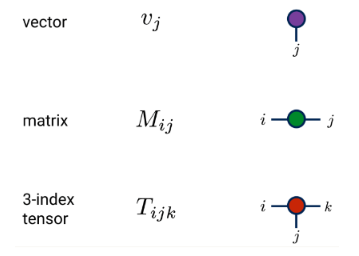
(2) Encolhimento do mesmo indicador
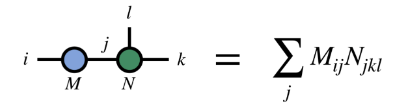
2. MPS
Para um sistema unidimensional com N pontos da grade, se cada ponto da grade tiver d estados quânticos, o espaço de Hilbert multicorpo pode ser expresso como o produto tensorial do espaço de Hilbert da grade:
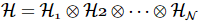
As posturas múltiplas arbitrárias correspondentes podem ser expressas como:
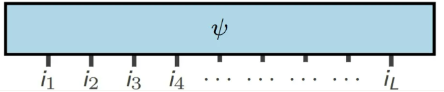
(Fonte da imagem: arXir:1603.03039, 2016)
A ideia central do estado de produto de matriz (MPS) é expressar o estado de múltiplos corpos como:
(Fonte da imagem: arXir:1603.03039, 2016)
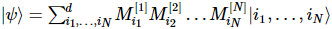
Cada unidade é um tensor de terceira ordem, no qual o índice físico é o estado quântico do ponto da grade, e o índice auxiliar pode ser considerado como o emaranhado quântico entre ele e os sistemas esquerdo e direito.
Decomposição SVD:
Para uma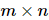 
matriz complexa geral A, existe uma decomposição tal que 
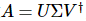, onde
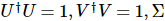é uma 
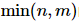matriz diagonal com dimensão e os elementos na diagonal são chamados de valores singulares. De modo geral, os valores singulares são organizados do maior para o menor ao longo da diagonal.
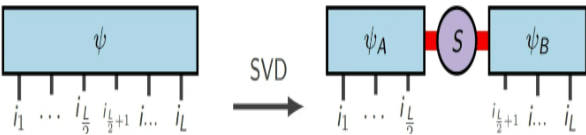
(Fonte da imagem: arXir:1603.03039, 2016)
Onde S representa valor singular. Se o emaranhado entre as duas partes do sistema não for forte, o espectro de valores singulares tende a decair rapidamente, e apenas menos valores singulares precisam ser retidos para reter a maior parte da informação da matriz. Suponha que estipulemos que cada grupo de decomposições de Schmidt retém não mais do que m valores singulares. No final, precisamos apenas de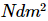 
um número real para representar aproximadamente esse estado multicorpo. Comparado com o método de representação original que requer 
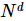1 parâmetro, esta representação tem uma complexidade de espaço linear para o número de pontos da grade, e a eficiência é muito maior do que a complexidade de crescimento exponencial da representação do produto tensorial original.
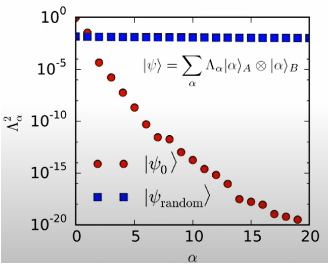
(Fonte da imagem: arXir:1603.03039, 2016)
O processo de obtenção do MPS:
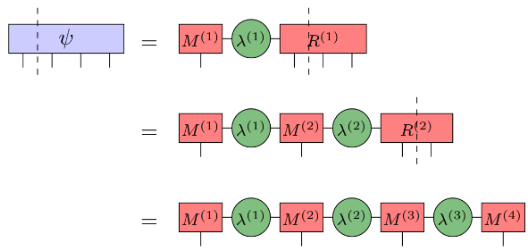
(Fonte da imagem: arXir:1603.03039, 2016)
PORQUE:
Para um operador de muitos corpos, como estados, podemos escrever o operador de muitos corpos na forma de produto matricial (MPO):
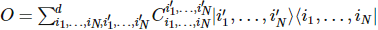
Diferente dos estados, o Hamiltoniano composto por operadores locais pode naturalmente ser escrito na forma de produtos matriciais:
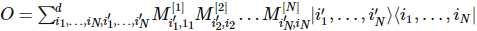
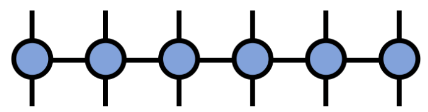
(Fonte da imagem: arXir:1603.03039, 2016)
O operador do produto da matriz ainda mantém a estrutura do produto da matriz após atuar no estado do produto da matriz:
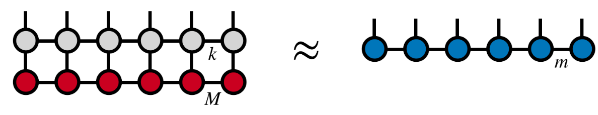
(Fonte da imagem: arXir:1603.03039, 2016)
03
Estados de rede de tensores isométricos em duas dimensões
1. Resumo
Os estados da rede tensorial são uma ferramenta promissora, mas numericamente desafiadora, para problemas quânticos bidimensionais de muitos corpos. Neste artigo, os autores apresentam TNS ansatz isometricamente restrito, uma forma que permite o encolhimento eficiente de redes tensores. Para avaliar numericamente o ansatz, os autores primeiro demonstraram que a representação MPS do estado fundamental do modelo de campo transversal bidimensional de Ising pode ser efetivamente convertida em isoTNS. Na verdade, os autores implementaram um algoritmo TEBD 2D e mostraram que ele efetivamente. encontra a forma isoTNS.
2. Estado da rede tensor isométrica
1) Condição de isometria: para uma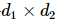 
matriz dimensional M, ou
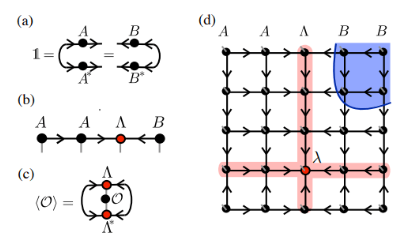
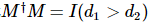. Nos diagramas de tensores, geralmente são usadas setas para indicar a ortogonalidade, o que estipula que a matriz unitária é obtida encolhendo o índice interno do tensor e seu tensor conjugado.
2) Forma canônica do MPS:
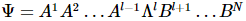
Entre eles, A e B satisfazem as condições ortogonais esquerda e direita. A condição ortogonal esquerda significa que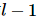 
a contração do quantum anterior e sua própria transposição é uma matriz unitária, e a condição ortogonal direita significa que 
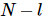a contração do quantum seguinte e sua própria transposição é uma matriz unitária, 
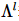representando um elemento diagonal decrescente. a matriz diagonal também é chamada de centro ortogonal.
3) O valor esperado da operação local pode ser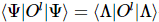 
obtido diretamente por, pois seu tensor AB externo encolhe para 1 de acordo com a condição de isometria.
(Fonte da imagem: Phys. Rev. Lett. 124, 037201)
- Generalize para duas dimensões:
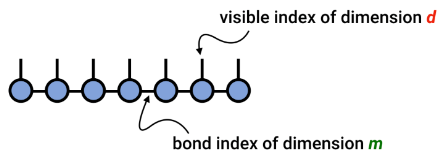
Por analogia com a fórmula acima, exigimos que cada linha e coluna do TNS seja uma isometria. Esta restrição pode ser ainda exigida exigindo que cada tensor seja uma isometria. Como mostrado na Figura d acima, a parte vermelha possui apenas setas para dentro. Portanto, esta é a "hipersuperfície ortogonal" unidimensional do TNS,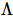 
que é a função de onda sob a base ortonormal padrão 
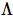. pode ser colocado em uma forma canônica unidimensional (seu centro ortogonal pode ser movido livremente usando o algoritmo canônico unidimensional). Para qualquer operador , existe
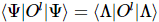, ou seja, há uma redução de dimensionalidade do valor esperado unidimensional que pode ser calculado de forma eficiente pelo algoritmo MPS padrão sem maiores aproximações. Isto contrasta fortemente com o TNS geral, onde o valor esperado requer o uso de uma redução aproximada de toda a rede.
3. Movendo hipersuperfície ortogonal
A forma ortogonal central só é computacionalmente útil se a hipersuperfície ortogonal Lammda puder ser movida eficientemente por toda a rede. Numa dimensão, podemos conseguir o movimento do centro ortogonal através da decomposição (QR ou SVD) de qualquer matriz ortogonal. Em duas dimensões, também precisamos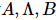 
mover a coluna inteira. Mas para sistemas bidimensionais, o método de decomposição de matriz ortogonal é inválido porque destrói 
a localidade necessária para ser expressa como um MPS.
(Fonte da imagem: Phys. Rev. Lett. 124, 037201)
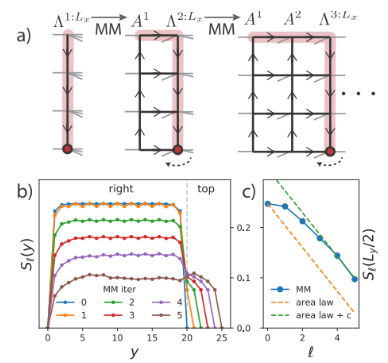
Neste artigo, o autor usa o método Moses Move para mover o centro da superfície ortogonal. Conforme mostrado na figura acima, após o algoritmo MM, a hipersuperfície ortogonal 
é dividida no produto dos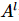 
estados ortogonais esquerdos e da coluna zero sem indicadores físicos 
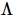. Entre eles, a descompressão é realizada aplicando continuamente o processo de “divisão” mostrado na Figura (b). O índice do ponto central 
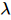é agrupado em três estados 
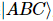e “dividido” em três tensores em duas etapas.
4. MPS estendido para isoNTS
(Fonte da imagem: Phys. Rev. Lett. 124, 037201)
Dada uma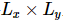 
função de onda do estado fundamental 
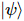, os autores propuseram um algoritmo iterativo que pode ser 
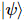colocado em isoTNS e 
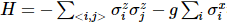testaram o modelo de campo transversal sing. Considere uma 
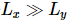faixa e use DMRG para obter 
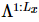o estado fundamental de um MPS 1D, onde cada “sítio” contém a linha correspondente de 
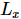spins [Figura (a)]. Conforme mostrado no terceiro painel da Figura a, o MM pode então ser usado para "dividir" iterativamente as colunas da função de onda 
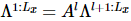, produzindo isoTNS. Neste exemplo, a dimensão da ligação é selecionada como 6. Quando g = 3,5 (fase paramagnética), o erro em cada local 
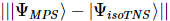é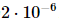 
. Nesse caso, 
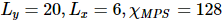. Os resultados são mostrados na Figura b, que mostra que a entropia de emaranhamento da segmentação ao longo da hipersuperfície ortogonal diminui à medida que o número de iterações aumenta. A Figura c ilustra que à medida que 
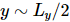o número de iterações aumenta, a entropia do emaranhamento decai linearmente, o que está de acordo com as expectativas.
5. 
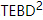Algoritmo
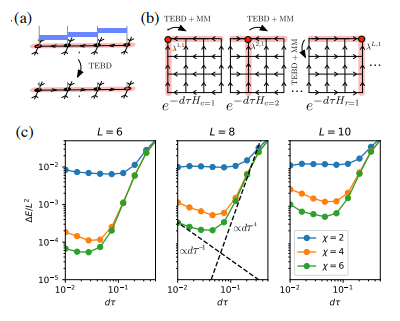
(Fonte da imagem: Phys. Rev. Lett. 124, 037201)
O autor também implementou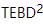 
o algoritmo. A idéia principal do TEBD é usar o algoritmo de recozimento baseado na decomposição de Trotter-Suzuki para evoluir o estado MPS inicializado aleatoriamente para o estado fundamental, converter o processo de evolução em um problema de encolhimento da rede tensorial e. use o algoritmo TEBD para resolver o encolhimento. Especificamente, um time stepper trotterizado é proposto para isoTNS, que pode obter o estado fundamental através da evolução do tempo virtual. Supondo que haja apenas interação com o vizinho mais próximo, dividimos o hamiltoniano em termos que atuam em colunas e linhas 
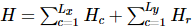e, em seguida, realizamos Trotterized 
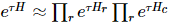, conforme mostrado na Figura (a). Para atualizações TEBD 1D, 
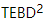pode ser facilmente melhorado para segunda ordem. Começamos 
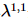a partir do centro ortogonal e, em seguida, movemos gradualmente o centro ortogonal chamando o algoritmo TEBD 1D padrão e o algoritmo MM. Em uma varredura, o algoritmo consiste, na verdade, em duas versões aninhadas de 1D TEBD, daí o nome 
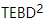. Entre eles, 
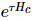a evolução de é alcançada pela chamada de 1D TEBD, e sua complexidade é a 
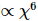de MM , enquanto a complexidade de atualização completa do PEPS irrestrito é de
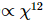. A Figura (c) mostra a densidade de erro de energia do modelo de Ising do campo transversal g = 3,5 
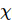em função do tamanho do passo de Trotter para diferentes tamanhos de sistema e dimensões máximas de ligação 
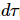. À medida que o tamanho da ligação 
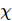aumenta, a energia mínima converge para o resultado exato.
04
Tomografia de estado quântico eficiente
1. Resumo
Inferir estados quânticos a partir de dados medidos torna-se inviável para sistemas maiores porque o número de medições e a quantidade de computação necessária para processá-las crescem exponencialmente com o tamanho do sistema. Neste artigo é proposto um esquema de tomografia mais vantajoso que a tomografia direta do tamanho do sistema. Este método requer manipulação uniforme de um número constante de subsistemas e depende apenas de um número linear de manipulações experimentais. Este esquema pode ser aplicado a uma ampla gama de estados quânticos, especialmente MPS.
2. Esquema baseado na transformação unitária
A ideia central deste método é encontrar uma sequência de operações para desembaraçar uma cadeia da esquerda para a direita. Cada operação nesta sequência é local e independente da dimensão N.
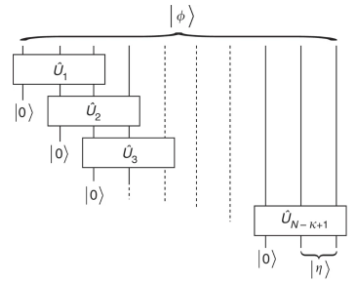
Suponha que o estado ideal seja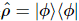 
, e assumimos que este estado quântico é um MPS com uma dada dimensão de ligação de R. O objetivo deste método é reconstruir isso 
.
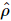Processo de algoritmo:
(Fonte da imagem: Nature Communications 1, 149 (2010))
1) Primeiro, pegamos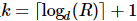 
e, em seguida, fazemos a tomografia de estado quântico padrão nos primeiros k locais, então a matriz de densidade reduzida dos primeiros k locais é:, 
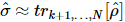esta matriz de densidade reduzida tem composição própria 
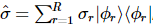, onde 
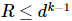,. Portanto, existe uma matriz de densidade com um qudit a menos cuja classificação R e soma dos autovalores 
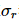são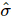 
iguais.
2) Em seguida, utilizamos ainda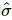 
as informações para construir uma matriz unitária para as primeiras k posições 
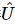, que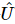 
pode desembaraçar o primeiro site.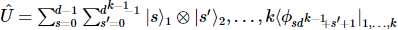
3) Aplique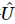 
a ação ao estado original para obter: 
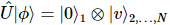Entre eles, 
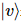existem alguns 
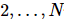estados puros em posição.
4) Em seguida, repita o processo acima para as próximas 2ª a k+1 posições. Por analogia, podemos obter uma sequência de matrizes unitárias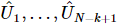 
, cada uma das quais 
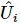atua em 
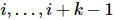posições. Essa sequência passa a ser 
, 
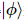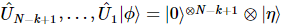onde cada um 
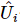atua em 
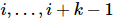posições. Esta sequência faz 
, 
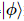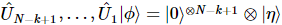onde,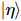 
estão alguns estados puros nas últimas k-1 posições.
Em resumo, este esquema deduz um circuito quântico para preparar MPS. A decomposição MPS pode ser facilmente obtida por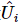 
e .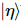
3. Erro
O erro deste método vem principalmente de dois aspectos. Um é a incapacidade de expressar completamente o estado quântico devido à limitação da dimensão da ligação, e o outro é o erro causado pela medição.
Dada uma matriz unitária desembaraçada estimada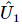 
, um estado arbitrário 
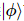pode ser expresso como:, 
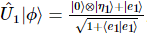onde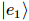 
está o vetor de erro.
Nas próximas etapas, podemos obter o estado na seguinte forma: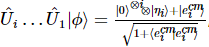 
, onde,
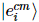é o erro cumulativo.
Podemos truncar esse vetor de erro medindo as primeiras i partículas na base padrão e pós-selecionando o resultado de todos os zeros. A probabilidade de isso acontecer é aproximadamente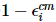 
, e deixa o sistema no estado 
.
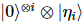Após uma série de transformações unitárias, o estado final é:
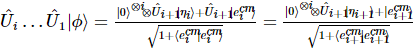
Entre eles,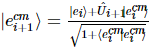 
portanto, 
.
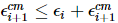Podemos descobrir que o erro se acumula linearmente com o número de partículas, e o MPS que obtemos é registrado como: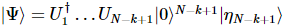 
, então temos: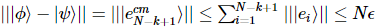
em,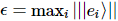 
. O erro global é, no máximo, a soma dos erros individuais em cada etapa.
Um programador nascido na década de 1990 desenvolveu um software de portabilidade de vídeo e faturou mais de 7 milhões em menos de um ano. O final foi muito punitivo! Google confirmou demissões, envolvendo a "maldição de 35 anos" dos programadores chineses nas equipes Flutter, Dart e . Python Arc Browser para Windows 1.0 em 3 meses oficialmente GA A participação de mercado do Windows 10 atinge 70%, Windows 11 GitHub continua a diminuir a ferramenta de desenvolvimento nativa de IA GitHub Copilot Workspace JAVA. é a única consulta de tipo forte que pode lidar com OLTP + OLAP. Este é o melhor ORM. Nos encontramos tarde demais.