Índice
1. Pontos de aprendizagem
Entenda a estratégia de pesquisa em profundidade de retrocesso.
Domine a estrutura algorítmica para resolver problemas usando o método de retrocesso
(1)Retrocesso recursivo
(2)Retrocesso iterativo
(3)Estrutura de algoritmo de árvore de subconjunto
(4)Estrutura de algoritmo de árvore de permutação
Aprenda estratégias de design para retrocesso por meio de exemplos aplicados.
(1) Problema de carregamento;
(2) Programação de tarefas em lote;
(3) Problema do triângulo sinalizado
(4) Problema de n-postes;
(5) Problema da mochila 0-1;
(6) Problema de clique máximo;
(7) m coloração de grafos Problema
(8) Problema do caixeiro viajante
(9) Problema de disposição do círculo
(10) Problema de disposição da placa de circuito
(11) Problema de postagem contínua
1.1 Método de retrocesso
Existem muitos problemas.Quando é necessário encontrar seu conjunto de soluções ou quando é necessário responder qual solução é a melhor solução que satisfaz certas restrições , o método de retrocesso é frequentemente usado .
O método básico de retrocesso é a pesquisa , ou um método de pesquisa exaustivo que seja bem organizado e possa evitar pesquisas desnecessárias . este métodoAdequado para resolver alguns problemas com um grande número de combinações. O método de retrocesso segue a estratégia de profundidade
na árvore do espaço de solução do problema .Pesquise a árvore do espaço de solução começando no nó raiz. Quando o algoritmo pesquisa qualquer ponto na árvore do espaço de soluções, ele primeiro determina se o nó contém a solução para o problema . Se definitivamente não estiver incluído, pule a busca pela subárvore com o nó como raiz e volte para seus nós ancestrais camada por camada ; caso contrário, entre na subárvore e continue pesquisando de acordo com a estratégia de profundidade em primeiro lugar .
1.2 Espaço de solução do problema
Vetor de solução do problema : O método de retrocesso espera que a solução de um problema possa ser expressa na forma de uma fórmula n-ária (x1, x2,...,xn).
Restrições explícitas : limites no valor do componente xi .
Restrições implícitas : Restrições impostas entre diferentes componentes para satisfazer a solução de um problema .
Espaço de solução : para uma instância do problema,Todas as tuplas cujos vetores de solução satisfazem restrições explícitas constituem um espaço de solução para esta instância.。
Nota: O mesmo problema pode ter múltiplas representações, e alguns métodos de representação são mais simples e requerem espaços de estado menores (menos armazenamento e métodos de pesquisa mais simples).
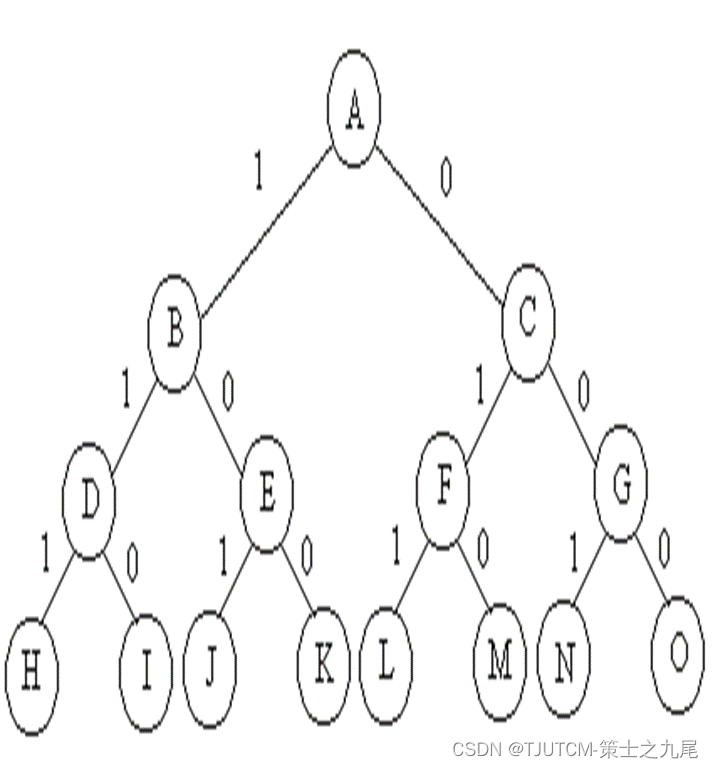
O espaço de solução do problema da mochila 0-1 quando n=3 é representado por uma árvore binária completa:
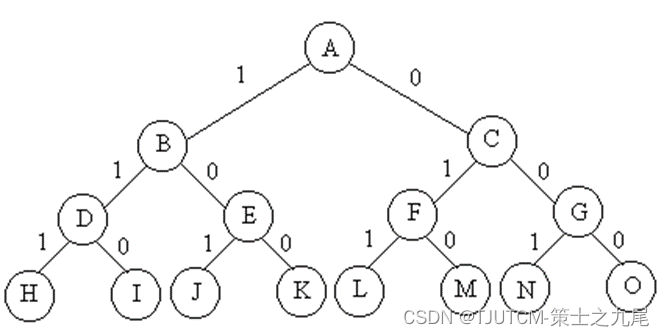
1.3 Espaço de solução do problema da mochila 0-1
O espaço de solução de um problema deve conter pelo menos uma solução (ótima) para o problema .
Para o problema da mochila 0-1 com n itens opcionais, o espaço de solução consiste em vetores 0-1 de comprimento n..
Quando n = 3, o espaço de solução é {(0,0,0),(0,0,1),(0,1,0),(0,1,1),(1,0,0) , (1,0,1),(1,1,0),(1,1,1)}
O espaço de soluções é na verdade o conjunto de soluções !
1.4 Espaço de solução do problema do caixeiro viajante
Pergunta: Um vendedor deseja ir a várias cidades para vender mercadorias e a distância (despesas de viagem) entre cada cidade é conhecida. Ele precisa escolher uma rota que comece na estação, passe por cada cidade e depois retorne à estação para minimizar a distância total (custo total da viagem).
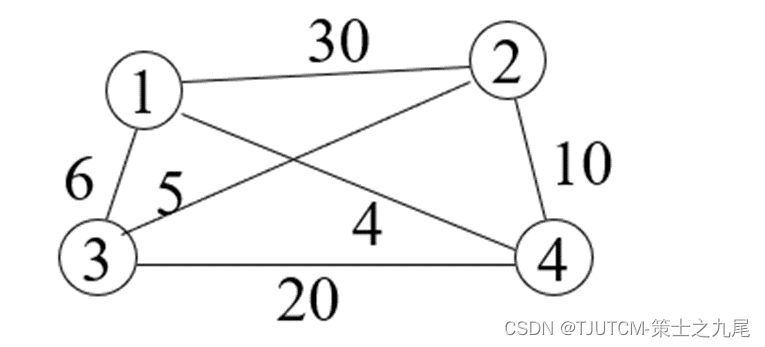
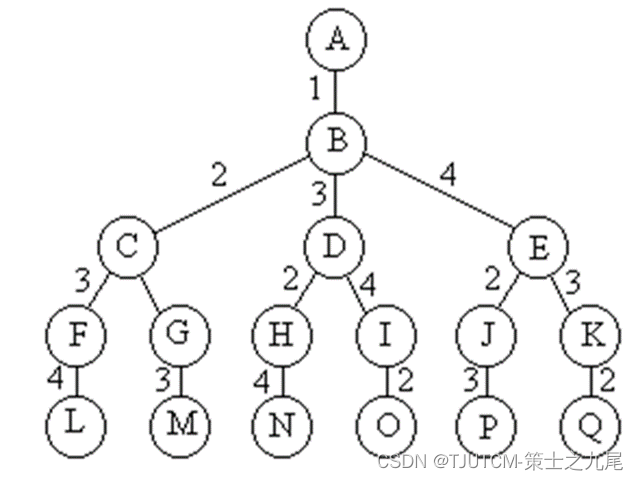
1.5 Método básico de geração do status do problema
Nó branco: um nó que não foi visitado .
Nó cinza: um nó que foi gerado, mas todos os seus filhos ainda não foram gerados, é chamado de nó cinza .
Nó preto: Um nó onde todos os filhos foram gerados é chamado de nó preto .
Método de geração de estado de problema em profundidade: Se for para um nó de extensão R, uma vez gerado seu filho C, C será considerado um novo nó de extensão. Depois de completar a busca exaustiva da subárvore C (a subárvore com raiz em C), transforme R novamente em um nó de extensão e continue a gerar o próximo filho de R (se existir).
Método amplo de geração de estado de problema: um nó estendido permanece um nó estendido até se tornar um nó preto.
Retrocesso: Para evitar a geração de estados problemáticos onde é impossível produzir a melhor solução, a função delimitadora deve ser usada continuamente para eliminar os nós ativos que são realmente impossíveis de produzir a solução necessária, de modo a reduzir a quantidade de cálculo do problema . O método de primeira geração em profundidade com funções limitadas é chamado de método de retrocesso
2. Ideia básica do método de retrocesso
(1) Para o problema em questão, defina o espaço de solução do problema ;
(2) Determine a estrutura do espaço de solução que seja fácil de pesquisar ;
(3) Pesquise o espaço de solução em profundidade e use funções de poda durante o processo de pesquisa para evitar pesquisas inválidas .
Funções de poda comumente usadas:
Use a função de restrição para podar as subárvores que não satisfazem as restrições no nó estendido ,
use a função delimitadora para podar as subárvores que não conseguem obter a solução ideal .
Uma característica distintiva do uso do método de retrocesso para resolver problemas é que o espaço de solução do problema é gerado dinamicamente durante o processo de busca . A qualquer momento, o algoritmo salva apenas o caminho do nó raiz até o nó de expansão atual . Se o comprimento do caminho mais longo do nó raiz ao nó folha na árvore do espaço de solução for h(n), o espaço computacional exigido pelo método de retrocesso é geralmente O(h(n)). O armazenamento explícito de todo o espaço da solução requer espaço de memória O(2h(n)) ou O(h(n)!) .
3. Condições aplicáveis do algoritmo de retrocesso
P(x1,x2,…,xk) é verdadeiro no nó <x1,x2,…,xk>. Ou seja, se o vetor <x1,x2,…,xk> satisfaz uma determinada propriedade, então existe P(x1,x2,…,xk+1)-> P(x1,x2,…,xk) 0<k <n. Chame isso de propriedades dominó .
┐ P(x1,x2,…,xk) ->┐ P(x1,x2,…,xk+1) 0<k<n O vetor k-dimensional não atende às condições de restrição e o vetor expandido para k
+ 1 dimensão ainda não atende às restrições. Só então você pode voltar atrás .
4. Retrocesso recursivo
O método de retrocesso realiza uma busca em profundidade no espaço de solução , portanto,Em geral, métodos recursivos são usados para implementar métodos de retrocesso.。
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=f(n,t);i<=g(n,t);i++) {
x[t]=h(i);
if (constraint(t)&&bound(t)) backtrack(t+1);
}
}
5. Retrocesso iterativo
usarAlgoritmo não recursivo de travessia em profundidade para árvores, o método de retrocesso pode ser expresso como um processo iterativo não recursivo .
void iterativeBacktrack ()
{
int t=1;
while (t>0) {
if (f(n,t)<=g(n,t))
for (int i=f(n,t);i<=g(n,t);i++) {
x[t]=h(i);
if (constraint(t)&&bound(t)) {
if (solution(t)) output(x);
else t++;}
}
else t--;
}
}
6. Árvore de subconjunto e árvore de permutação
Quando o problema dado é encontrar um subconjunto que satisfaça uma determinada propriedade de um conjunto S de n elementos , a árvore do espaço de solução correspondente é chamada de árvore de subconjunto (2n).
Quando o problema dado é determinar o arranjo de n elementos que satisfazem uma determinada propriedade , a árvore do espaço de solução correspondente é chamada de árvore de arranjo (n!).
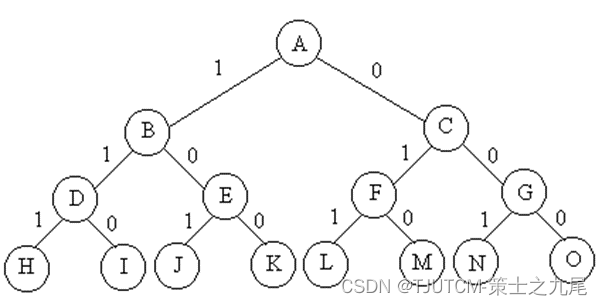
Atravessar a árvore de subconjuntos requer tempo de computação O(2n)。
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=0;i<=1;i++) {
x[t]=i;
if (legal(t)) backtrack(t+1);
}
}
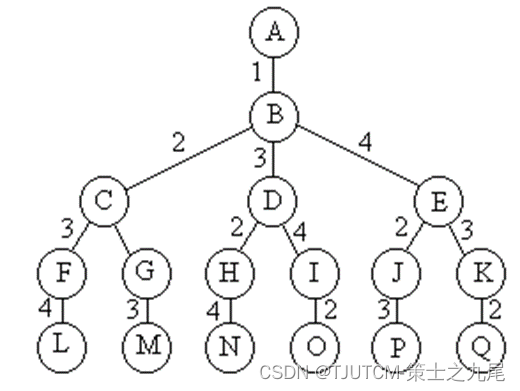
Atravessar a árvore de permutação requer tempo de computação O(n!)。
void backtrack (int t)
{
if (t>n) output(x);
else
for (int i=t;i<=n;i++) {
swap(x[t], x[i]);
if (legal(t)) backtrack(t+1);
swap(x[t], x[i]);
}
}
7. Problemas de carregamento
Há um lote de n contêineres a serem carregados em dois navios com capacidades de carga c1 e c2 respectivamente. O peso do contêiner i é wi e 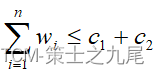 .
.
O problema de carregamento requer determinar se existe um plano de carregamento razoável que possa carregar este contêiner nesses dois navios.. Nesse caso, encontre uma solução de carregamento.
Encher o primeiro navio tanto quanto possível equivale a selecionar um subconjunto de todos os contêineres de modo que a soma dos pesos dos contêineres no subconjunto seja a mais próxima . Pode-se observar que o problema de carregamento é equivalente ao seguinte problema especial da mochila 0-1.
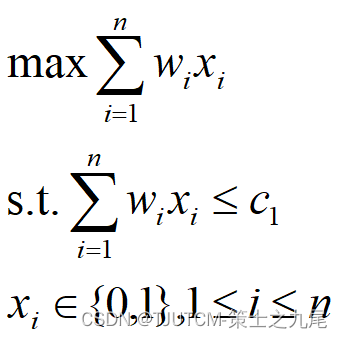
Use o método de retrocesso para projetar um algoritmo de tempo computacional O(2n) para resolver o problema de carregamento. Este algoritmo é superior aos algoritmos de programação dinâmica em alguns casos .
Quando n=3, c1=c2=50 e w=[10,40,40]
se w=[20,40,40]
Plano de carregamento ideal:
(1) Primeiro encha o primeiro navio o máximo possível ;
(2) Carregue os contêineres restantes no segundo navio .
Espaço de solução: árvore de subconjuntos .
Função de restrição de viabilidade (selecione o elemento atual):
Função de limite superior (não seleciona o elemento atual):
A capacidade de carga atual cw + o peso do contêiner restante r ≤ a capacidade de carga ótima atual melhorada .
void backtrack (int i)
{
// 搜索第i层结点
if (i > n) // 到达叶结点
更新最优解bestx,bestw;return;
r -= w[i];
if (cw + w[i] <= c) {
// 搜索左子树
x[i] = 1;
cw += w[i];
backtrack(i + 1);
cw -= w[i]; }
if (cw + r > bestw) {
x[i] = 0; // 搜索右子树
backtrack(i + 1); }
r += w[i];
}
8. Problemas de agendamento de trabalhos em lote
n tarefas {1, 2,…, n} devem ser processadas em duas máquinas. Cada tarefa deve ser processada primeiro pela máquina 1 e depois pela máquina 2. O tempo necessário para a máquina 1 processar a tarefa i é ai, e a máquina 2 O tempo necessário para processar o trabalho i é bi (1≤i≤n).O problema de agendamento de trabalho em lote requer a determinação da ordem de processamento ideal desses n trabalhos , de modo que, começando do primeiro trabalho sendo processado na máquina 1, até o último trabalho O final do processamento leva menos tempo na máquina 2.
Obviamente,Um cronograma ideal para tarefas de processamento em lote deve garantir que a máquina 1 não tenha tempo ocioso e a máquina 2 tenha o menor tempo ocioso.. Pode ser provado que existe um cronograma de trabalho ideal tal que os trabalhos na máquina 1 e na máquina 2 sejam concluídos na mesma ordem .
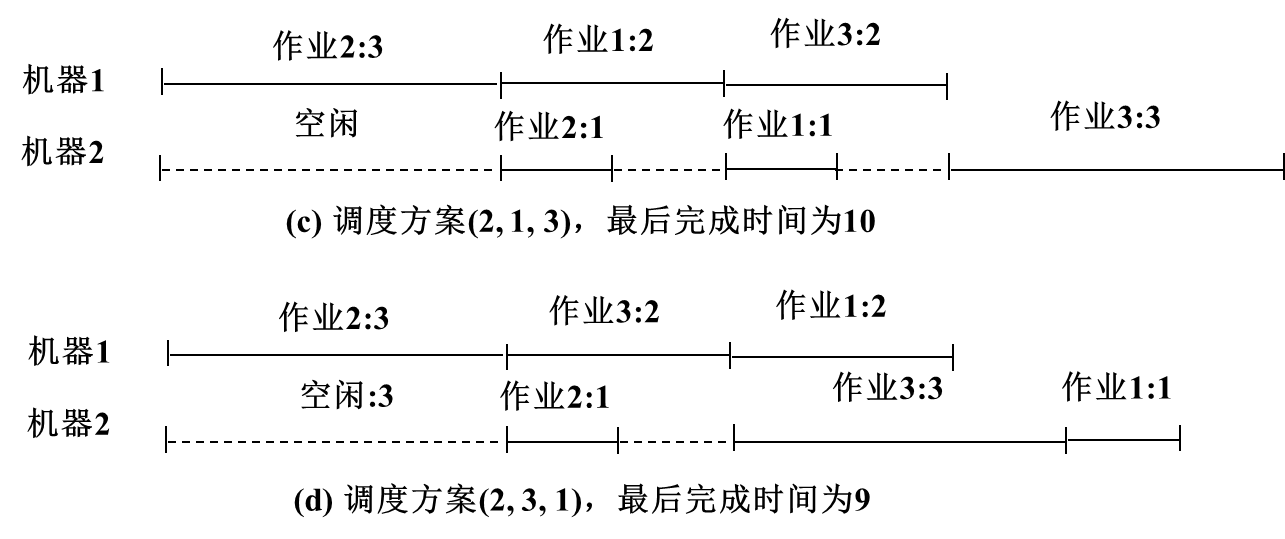
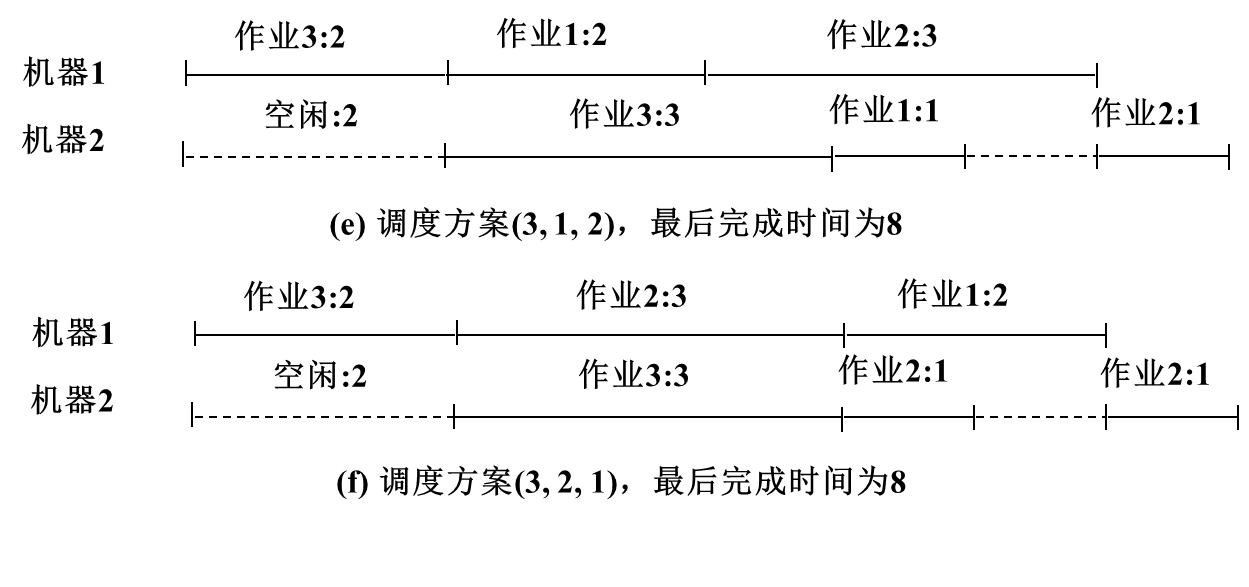
Exemplo: Existem três trabalhos {1, 2, 3}. O tempo de processamento necessário para esses três trabalhos na máquina 1 é (2, 3, 2) e o tempo de processamento necessário na máquina 2 é (1, 1, 3) , então as soluções de escalonamento ideais são (1, 3, 2), (3, 1, 2) e (3, 2, 1), e seu tempo de conclusão é 8.

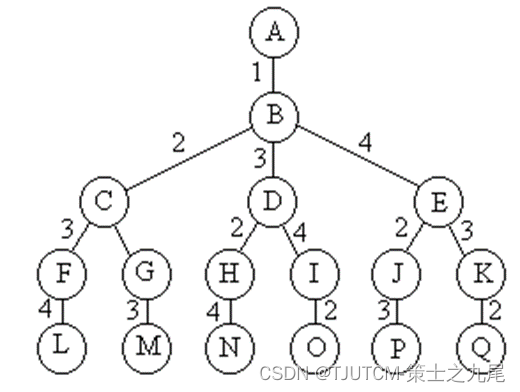
Espaço de solução: árvore de permutação .
void Flowshop::Backtrack(int i)
{
if (i > n) {
for (int j = 1; j <= n; j++)
bestx[j] = x[j];
bestf = f;
}
else
for (int j = i; j <= n; j++) {
f1+=M[x[j]][1];
f2[i]=((f2[i-1]>f1)?f2[i-1]:f1)+M[x[j]][2];
f+=f2[i];
if (f < bestf) {
Swap(x[i], x[j]);
Backtrack(i+1);
Swap(x[i], x[j]);
}
f1- =M[x[j]][1];
f- =f2[i];
}
}
class Flowshop {
friend Flow(int**, int, int []);
private:
void Backtrack(int i);
int **M, // 各作业所需的处理时间
*x, // 当前作业调度
*bestx, // 当前最优作业调度
*f2, // 机器2完成处理时间
f1, // 机器1完成处理时间
f, // 完成时间和
bestf, // 当前最优值
n; // 作业数};