Guia de referência pymoo do pacote de algoritmo de otimização multiobjetivo

Guia de referência pymoo do pacote de algoritmo de otimização multiobjetivo

1 Definição de função multiobjetivo

Sem perder generalidade, o problema de otimização pode ser definido como:

Na fórmula:

• $x_{}$Parte $i$ variáveis​​a serem otimizadas;
• $x_{eu}^{}$和$x_{eu}^{}$como seus limites inferior e superior ;
• $f_{}$é $m$ funçõesobjetivo;
• $g_{}$Para o $j$ restriçõesde desigualdade;
• $h_{}$Para o $k$ restriçõesde igualdade.

função objetivo $f$ deve satisfazer todas as restrições de igualdade e desigualdade. Se uma função objetivo específica émaximizar($máx.f_{}$), o problema pode ser redefinido para minimizar seu valor negativo ( $\min -f{\_}_{}$)。

Os seguintes aspectos precisam ser considerados em problemas de otimização:

1) Tipo de variável

As variáveis ​​cobrem o espaço de busca Ω do problema de otimização . Diferentes tipos de variáveis, como contínua, discreta/inteira, binária ou permutação, definem as características do espaço de busca. Em alguns casos, os tipos de variáveis ​​podem até ser misturados, acrescentando ainda mais complexidade.

2) Número de variáveis

Não só o tipo, mas também o número de variáveis ​​(N) é essencial. Você pode imaginar que resolver um problema com apenas dez variáveis ​​é completamente diferente de resolver um problema com milhares de variáveis. Para problemas de otimização em larga escala, onde até mesmo o cálculo de derivadas de segunda ordem é muito caro, o manuseio eficiente da memória desempenha um papel mais importante.

3) Quantidade alvo

Alguns problemas de otimização têm múltiplos objetivos conflitantes (M>1) a serem otimizados .

A otimização de objetivo único é apenas um caso especial de M=1. Na otimização multiobjetivo, a solução rege a comparação de escalares na otimização de objetivo único. Existem múltiplas dimensões no espaço alvo, e o ótimo (na maioria das vezes) consiste em um conjunto de soluções não dominadas. Algoritmos baseados em populações são usados ​​principalmente como solucionadores porque um conjunto de soluções deve ser obtido.

4) Restrições

Existem dois tipos de restrições em problemas de otimização : restrições de desigualdade (g) e restrições de igualdade (h) .

Por mais bem objetiva que seja uma solução, ela é considerada inviável se acabar violando apenas uma restrição .

As restrições têm um forte impacto na complexidade do problema. Por exemplo, se apenas algumas soluções no espaço de busca forem viáveis, ou se um grande número de restrições (|J|+|K|) precisar ser satisfeito. Para algoritmos genéticos , satisfazer as restrições de igualdade é bastante desafiador. Portanto, este problema precisa ser resolvido de diferentes maneiras, por exemplo, mapeando o espaço de busca para um espaço de utilidade que sempre satisfaça as restrições de igualdade , ou customizando a injeção de conhecimento das restrições de igualdade .

5) Multimodal

Em cenários de aptidão multimodais, a otimização torna-se mais difícil devido à existência de um pequeno ou mesmo grande número de ótimos locais . Para uma solução encontrada, deve-se sempre perguntar se o método explora uma área suficiente do espaço de busca para maximizar a probabilidade de obtenção do ótimo global . Os espaços de busca multimodais revelam rapidamente as limitações da busca local e podem facilmente travar .

6) Diferenciabilidade

Uma função diferenciável significa que a primeira e até a segunda derivada podem ser calculadas . Funções diferenciáveis ​​permitem o uso de métodos de otimização baseados em gradiente , que apresentam vantagens significativas sobre métodos sem gradiente. A maioria dos algoritmos baseados em gradiente são pontuais e muito eficientes para cenários de aptidão monomodal. Na prática, entretanto , as funções muitas vezes não são diferenciáveis , ou funções mais complexas requerem pesquisa global em vez de pesquisa local . O campo de pesquisa que resolve problemas sem conhecer a otimização matemática também é conhecido como otimização de caixa preta .

7) Incerteza.

As funções objetivo e de restrição são geralmente consideradas determinísticas . No entanto, se uma ou mais funções objetivo são incertas, isso introduz ruído ou também é conhecido como incerteza . Uma técnica para considerar a aleatoriedade potencial é repetir a avaliação com diferentes sementes aleatórias e calcular a média dos valores resultantes . Além disso, o desvio padrão derivado de múltiplas avaliações pode ser usado para determinar o desempenho e a confiabilidade de uma solução específica . De modo geral, problemas de otimização com incerteza potencial são estudados pela área de pesquisa de otimização estocástica.

2 Problema de otimização biobjetivo

Problema de otimização biobjetivo:

Entre as questões acima:

• Existem duas funções objetivo ( $M=2$ ), queminimiza $f_{}\left(x\right)$ ,maximizar $f_{}\left(x\right)$。
• Existem duas restrições de desigualdade no objetivo de otimização ( $J.=2$ ), onde$g_{}\left(x\right)$ émenor ou igual a,$g_{}\left(x\right)$ émaior ou igual a.
• O problema é definido por duas variáveis ​​( $N=2$ ),$x_{}$e $x_{}$, ambos variam em $[-2,2]$。
• Este problema de otimização não contém restrições de igualdade ( $K=0$ )。

Primeiro analise a localização da solução ótima de Pareto.

$f_{}$O valor mínimode$($$x$$)$ está em$(0,0)$ ,$f_{}$O valor máximode$($$x$$)$ está em$(1,0)$ lugar. Como ambas as funçõessão quadráticas, a solução ótimaé dada por uma linha reta entre as duas soluções ótimas. Isso significa que todas as soluções pareto ótimas (ignorando as restrições por enquanto) têm$x_{}=0$和$x1\in (0,1)$。

A primeira restrição depende apenas de $x_{}$, e satisfaz $x_{}\in (\mathrm{0,1},\_\_0.9)$。$x_{}\in (\mathrm{0,4},\_\_0.6)\; satisfaza$ segunda restriçãog 2$g\_2$$g_{}$. Isto significa que, de uma perspectiva analítica, o conjunto ótimo de Pareto é:

$$PS\_=\left\{\left(x_{},x_{}\right)|\left(\mathrm{0,1}\_\_\le x_{}\le 0.4\right)\vee \left(0.6\_\_\le x_{}\le 0.9\right)\wedge x_{}=0\right\}$$

Veja o conjunto ideal de Pareto (laranja) traçando a função:

import numpy as np

X1, X2 = np.meshgrid(np.linspace(-2, 2, 500), np.linspace(-2, 2, 500))

F1 = X1**2 + X2**2
F2 = (X1-1)**2 + X2**2
G = X1**2 - X1 + 3/16

G1 = 2 * (X1[0] - 0.1) * (X1[0] - 0.9)
G2 = 20 * (X1[0] - 0.4) * (X1[0] - 0.6)


import matplotlib.pyplot as plt
plt.rc('font', family='serif')

levels = [0.02, 0.1, 0.25, 0.5, 0.8]
plt.figure(figsize=(7, 5))
CS = plt.contour(X1, X2, F1, levels, colors='black', alpha=0.5)
CS.collections[0].set_label("$f_1(x)$")

CS = plt.contour(X1, X2, F2, levels, linestyles="dashed", colors='black', alpha=0.5)
CS.collections[0].set_label("$f_2(x)$")

plt.plot(X1[0], G1, linewidth=2.0, color="green", linestyle='dotted')
plt.plot(X1[0][G1<0], G1[G1<0], label="$g_1(x)$", linewidth=2.0, color="green")

plt.plot(X1[0], G2, linewidth=2.0, color="blue", linestyle='dotted')
plt.plot(X1[0][X1[0]>0.6], G2[X1[0]>0.6], label="$g_2(x)$",linewidth=2.0, color="blue")
plt.plot(X1[0][X1[0]<0.4], G2[X1[0]<0.4], linewidth=2.0, color="blue")

plt.plot(np.linspace(0.1,0.4,100), np.zeros(100),linewidth=3.0, color="orange")
plt.plot(np.linspace(0.6,0.9,100), np.zeros(100),linewidth=3.0, color="orange")

plt.xlim(-0.5, 1.5)
plt.ylim(-0.5, 1)
plt.xlabel("$x_1$")
plt.ylabel("$x_2$")

plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.12),
          ncol=4, fancybox=True, shadow=False)

plt.tight_layout()
plt.show()

Em seguida, a frente de Pareto é derivada mapeando o conjunto de Pareto para o espaço alvo. Equação de Pareto-frente baseada em $f_{}$e depende de $f_{}$Variáveis.

Sabemos que o valor ideal é $x_{}=0$ Isso significa que a função objetivo pode ser simplificada para$f_{}\left(x\right)=100x_1^{},f_{}\left(x\right)=-(x_{}-1{)}^2$ . O primeiro alvo$f_{}$Pode ser convertido em $x_{}=\sqrt{\frac{f_{}}{100}}$e, em seguida, coloque o segundo alvo, o resultado é:

$$f_{}=-{\left(\sqrt{\frac{f_{}}{100}}-1\right)}^2$$

A equação define a forma. Em seguida, precisamos definir $f_{}$todos os valores possíveis de . Se $x_{}$Substitua o valor de $f_{}$, você obterá os pontos de interesse $[1,16]$ e[36, 81] [36,81$]$$[36,81]$ . Portanto, frente de Pareto é:

import numpy as np
import matplotlib.pyplot as plt

plt.figure(figsize=(7, 5))

f2 = lambda f1: - ((f1/100) ** 0.5 - 1)**2
F1_a, F1_b = np.linspace(1, 16, 300), np.linspace(36, 81, 300)
F2_a, F2_b = f2(F1_a), f2(F1_b)

plt.rc('font', family='serif')
plt.plot(F1_a,F2_a, linewidth=2.0, color="green", label="Pareto-front")
plt.plot(F1_b,F2_b, linewidth=2.0, color="green")

plt.xlabel("$f_1$")
plt.ylabel("$f_2$")

plt.legend(loc='upper center', bbox_to_anchor=(0.5, 1.10),
          ncol=4, fancybox=True, shadow=False)

plt.tight_layout()
plt.show()

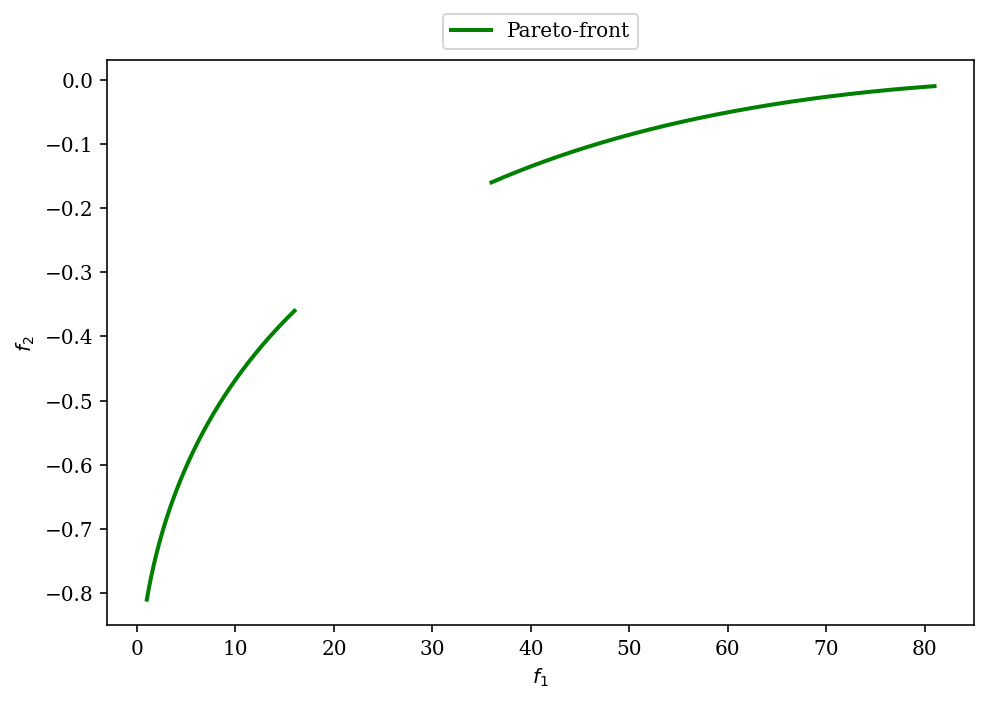
Pode-se observar pela figura que se trata de um conjunto não dominado. Para este problema de otimização, o primeiro objetivo é minimizar, o segundo objetivo é maximizar e a melhor solução está no canto superior esquerdo.

3 Use pymoo para otimizar o alvo

A maioria das estruturas de otimização se esforçam para minimizar ou maximizar todos os objetivos e possuem apenas restrições ≤ ou ≥ . Em pymoo, toda função objetivo deve ser mínima e toda restrição precisa ser fornecida na forma ≤0 .

Portanto, é preciso −1multiplicar um objetivo que deve ser maximizado e depois minimizá-lo. Isso leva à minimização $-f{\_}_{}\left(x\right)$ em vez de maximizar$f_{}\left(x\right)$。

Além disso, as restrições de desigualdade precisam ser expressas como 小于零(≤0)restrições. Portanto, $g_{}\left(x\right)$−1 parainvertera relação de desigualdade.

Além disso, recomenda-se normalizar as restrições para que operem na mesma escala e lhes dê igual importância. Para $g_{}\left(x\right)$ , o coeficiente é$2\cdot (-0,1)\_\_\_\cdot (-0,9)\_\_\_=0.18$，$g_{}\left(x\right)$ , o coeficiente é$20\cdot (-0,4)\_\_\_\cdot (-0,6)\_\_\_=4.8$ .

Usando $g_{}\left(x\right)$ e$g_{}\left(x\right)$ é dividido pelo seu coeficiente correspondentepara normalizar as restrições.

A função objetivo final é:

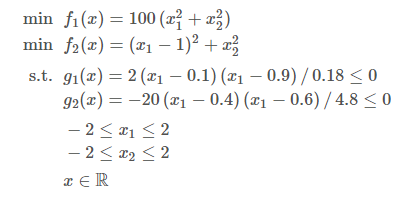
instalação do Pymoo:

pip install -U pymoo

1) Definição de problema baseado em elementos

ElementwiseProblemUm novo destino Python herdado é definido e as propriedades corretas são definidas, como o número de alvos (n_obj) e o número de restrições (n_constr) , bem como o limite inferior (xl) e o limite superior (xu) .

A função responsável pela avaliação é _evaluate. A interface da função é o parâmetro $x$和$fora$ .$\_$$\_$Para esta implementação baseada em elemento,$x$ é uman_varmatriz NumPy unidimensional de comprimento que representa a solução única a ser calculada. $out$ é um dicionário.

Os valores alvo devem ser n_objescritos como uma lista de comprimento da matriz NumPy out["F"]e as restrições devem ser escritas como uma lista de n_constrcomprimento out["G"].

import numpy as np
from pymoo.core.problem import ElementwiseProblem

class MyProblem(ElementwiseProblem):

    def __init__(self):
        super().__init__(n_var=2,
                         n_obj=2,
                         n_constr=2,
                         xl=np.array([-2,-2]),
                         xu=np.array([2,2]))

    def _evaluate(self, x, out, *args, **kwargs):
        f1 = 100 * (x[0]**2 + x[1]**2)
        f2 = (x[0]-1)**2 + x[1]**2

        g1 = 2*(x[0]-0.1) * (x[0]-0.9) / 0.18
        g2 = - 20*(x[0]-0.4) * (x[0]-0.6) / 4.8

        out["F"] = [f1, f2]
        out["G"] = [g1, g2]


problem = MyProblem()

Um problema pode ser definido de diversas maneiras diferentes. O texto acima demonstra uma implementação baseada em elementos, o que significa que para cada solução $x$ chama _avaliar.

Outra abordagem é vetorizada, onde $x$ representaum conjunto completo de soluçõesou uma abordagem funcional, possivelmente mais pitônica, que fornece cada objetivo e restrição na forma de uma função.

Para obter detalhes, consulte:

https://pymoo.org/problems/definition.html

2) Algoritmo de inicialização

Lista de algoritmos pymoo:

algoritmo
1. Algoritmo genético GA , objetivo único
2. Evolução diferencial DE, objetivo único
3. Algoritmo genético de chave aleatória tendencioso BRKGA, objetivo único
4. Simplex NelderMead, alvo único
5. Pesquisa de padrão PatternSearch, alvo único
6. CMAES, alvo único
7. Estratégia de evolução ES, objetivo único
8. Estratégia de evolução de classificação aleatória SRES, objetivo único
9. Estratégia de evolução de classificação aleatória aprimorada ISRES, objetivo único
10. NSGA-II, NSGA2, alvos múltiplos
11. R-NSGA-II, RNSGA2, multialvo
12. NSGA-III, NSGA3, alvos múltiplos
13. U-NSGA-III, UNSGA3, alvo único e alvos múltiplos
14. R-NSGA-III, RNSGA3, alvo único e alvo múltiplo
15. Decomposição multi-alvo MOEAD, alvo único e multi-alvo
16. AGE-MOEA, alvo único e alvos múltiplos
17. C-TAEA, alvo único e alvos múltiplos

Para obter detalhes, consulte:

https://pymoo.org/algorithms/list.html#nb-algorithms-list

O algoritmo multiobjetivo NSGA-II é selecionado aqui para explicação. Para a maioria dos algoritmos, você pode escolher os hiperparâmetros padrão ou criar sua própria versão do algoritmo modificando-os.

Por exemplo, para este problema relativamente simples, escolha um tamanho de população de 40 ( pop_size=40) e apenas 10 descendentes por geração ( ) n_offsprings=10). Habilite a verificação duplicada ( eliminate_duplicate =True) para garantir que os acasalamentos produzam descendentes que diferem tanto dos seus próprios valores quanto dos valores do espaço de projeto da população existente .

from pymoo.algorithms.moo.nsga2 import NSGA2
from pymoo.factory import get_sampling, get_crossover, get_mutation

algorithm = NSGA2(
    pop_size=40,
    n_offsprings=10,
    sampling=get_sampling("real_random"),
    crossover=get_crossover("real_sbx", prob=0.9, eta=15),
    mutation=get_mutation("real_pm", eta=20),
    eliminate_duplicates=True
)

3) Defina critérios de rescisão

Além disso, os critérios de terminação precisam ser definidos para iniciar o processo de otimização. A maneira mais comum de definir terminação é limitar o número total de avaliações da função ou simplesmente limitar o número de iterações do algoritmo .

Além disso, alguns algoritmos implementaram seus próprios algoritmos, como Nelder-Mead quando o simplex degenera, ou CMA-ES ao usar bibliotecas de fornecedores. Devido à simplicidade do problema, um algoritmo bastante pequeno de 40 iterações foi utilizado

from pymoo.factory import get_termination
termination = get_termination("n_gen", 40)

Para obter uma lista e explicação dos critérios de rescisão, consulte:

https://pymoo.org/interface/termination.html

4) Otimização

Finalmente, o problema é resolvido com um algoritmo definido e terminação. As interfaces funcionais usam a abordagem de minimização .

Por padrão, o algoritmo de execução da função é minimizado e as cópias profundas dos objetos são encerradas para garantir que não sejam modificadas durante as chamadas de função . Isso é importante para garantir que chamadas de função repetidas com a mesma semente aleatória acabem com o mesmo resultado. Quando o algoritmo termina, a função de minimização retorna um objeto Result.

from pymoo.optimize import minimize

res = minimize(problem,
               algorithm,
               termination,
               seed=1,
               save_history=True,
               verbose=True)

X = res.X
F = res.F

Cada linha na figura acima representa uma iteração. As duas primeiras colunas são o contador de construção atual e o número de cálculos até o momento. Para problemas restritos, a terceira e quarta colunas mostram a violação mínima da restrição ( cv (min)) e a violação média da restrição ( cv (avg)) na população atual. A seguir está o número de soluções não dominadas ( n_nds) e outros dois indicadores que representam o movimento no espaço alvo.

5) Visualização

import matplotlib.pyplot as plt
xl, xu = problem.bounds()
plt.figure(figsize=(7, 5))
plt.scatter(X[:, 0], X[:, 1], s=30, facecolors='none', edgecolors='r')
plt.xlim(xl[0], xu[0])
plt.ylim(xl[1], xu[1])
plt.title("Design Space")
plt.show()

F = res.F
xl, xu = problem.bounds()
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.title("Objective Space")
plt.show()

4 Tomada de decisão multicritério

Depois de obter um conjunto de soluções não dominadas, como o tomador de decisão determina esse conjunto de soluções em poucas ou mesmo em uma única solução? Este processo de tomada de decisão para problemas multiobjetivos também é chamado de tomada de decisão multicritério (MCDM).

1) Normalização do valor da função objetivo

Na otimização multiobjetivo, a escala da função objetivo precisa ser considerada :

fl = F.min(axis=0)
fu = F.max(axis=0)
print(f"Scale f1: [{
      
      fl[0]}, {
      
      fu[0]}]")
print(f"Scale f2: [{
      
      fl[1]}, {
      
      fu[1]}]")

# Scale f1: [1.3377795039158837, 74.97223429467643]
# Scale f2: [0.01809179532919018, 0.7831767823138299]

Pode-se ver que o alvo $f_{}$e $f_{}$Os limites superior e inferior são muito diferentes e precisam ser normalizados.

Sem padronização, estamos comparando laranjas e maçãs. O primeiro alvo dominará qualquer cálculo de distância no espaço alvo devido ao seu tamanho maior . Lidar com alvos de diferentes tamanhos é uma parte inerente de qualquer algoritmo multiobjetivo, portanto o mesmo precisa ser feito para o pós-processamento.

Uma abordagem comum é usar os chamados pontos ideais e nadir para especificação . Supõe-se aqui que o ponto ideal e o ponto mais baixo (também chamado de ponto limite) e a frente de Pareto são desconhecidos. Portanto, esses pontos podem ser aproximados como:

approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(approx_ideal[0], approx_ideal[1], facecolors='none', edgecolors='red', marker="*", s=100, label="Ideal Point (Approx)")
plt.scatter(approx_nadir[0], approx_nadir[1], facecolors='none', edgecolors='black', marker="p", s=100, label="Nadir Point (Approx)")
plt.title("Objective Space")
plt.legend()
plt.show()

Os valores alvo são normalizados por:

nF = (F - approx_ideal) / (approx_nadir - approx_ideal)

fl = nF.min(axis=0)
fu = nF.max(axis=0)
print(f"Scale f1: [{
      
      fl[0]}, {
      
      fu[0]}]")
print(f"Scale f2: [{
      
      fl[1]}, {
      
      fu[1]}]")

plt.figure(figsize=(7, 5))
plt.scatter(nF[:, 0], nF[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.title("Objective Space")
plt.show()

# Scale f1: [0.0, 1.0]
# Scale f2: [0.0, 1.0]

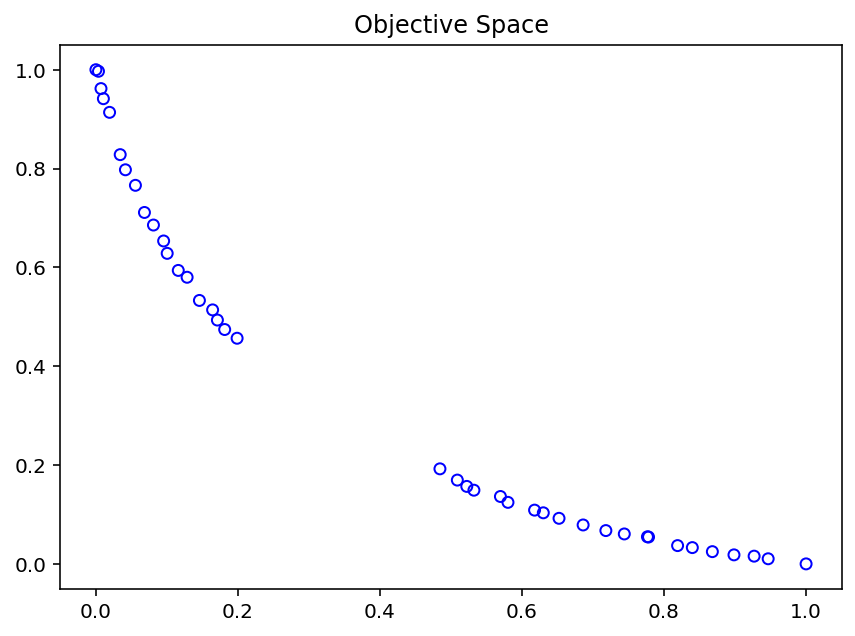
2) Programação de compromisso

Uma maneira de tomar decisões é usar funções de decomposição . É necessário definir pesos que reflitam os desejos do usuário . Os pesos dados pelo vetor são apenas números positivos de ponto flutuante somando 1 , com comprimento igual ao número alvo . Para um problema de duplo objetivo, assumindo que o primeiro objetivo não é tão importante quanto o segundo objetivo, defina o peso:

weights = np.array([0.2, 0.8])

Em seguida, escolha o método de decomposição Augmented Scalarization Function (ASF).

from pymoo.decomposition.asf import ASF
decomp = ASF()

Como a PSA deve ser minimizada , o menor valor da PSA é selecionado entre todas as soluções .

Por que os pesos não são passados ​​diretamente, mas sim 1/pesos? Para o ASF, existem diferentes fórmulas, uma onde os valores são divididos e outra onde os valores são multiplicados. Em "pymoo", "divide" não reflete os padrões do usuário. Portanto, a função inversa precisa ser aplicada.

i = decomp.do(nF, 1/weights).argmin()

Depois de encontrar a solução ( $i$ ), o resultado pode ser expresso em sua proporção original:

print("Best regarding ASF: Point \ni = %s\nF = %s" % (i, F[i]))

plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()

# Best regarding ASF: Point
# i = 21
# F = [43.28059434  0.12244878]

Um benefício desta abordagem é que qualquer tipo de função de decomposição pode ser usada.

3) Pseudo-Pesos

Em um contexto de otimização multiobjetivo, um método simples para selecionar soluções de um conjunto de soluções é o método do vetor de pseudopesos. Calcule o iith respectivamentePseudo pesoswi w_i$de\; i\; funções\; objetivo$$c_{}$：

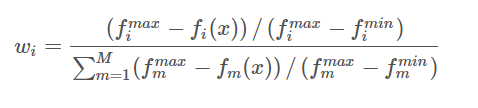
Esta equação calcula cada objetivo ii A distância normalizada de$i$ até a pior solução . Observe que paraconjuntos de Pareto não convexos, os pseudopesos não correspondem aos resultados da otimização usando somas ponderadas. Porém, paraum conjunto de Pareto convexo, os pseudopesos representam posições no espaço alvo.

from pymoo.mcdm.pseudo_weights import PseudoWeights
i = PseudoWeights(weights).do(nF)
print("Best regarding Pseudo Weights: Point \ni = %s\nF = %s" % (i, F[i]))

plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='blue')
plt.scatter(F[i, 0], F[i, 1], marker="x", color="red", s=200)
plt.title("Objective Space")
plt.show()

# Best regarding Pseudo Weights: Point
# i = 39
# F = [58.52211061  0.06005482]

5 Análise de convergência

A análise de convergência deve considerar dois casos, i) o conjunto de Pareto é desconhecido, ou ii) o conjunto de Pareto foi derivado analiticamente, ou existe uma aproximação razoável.

1) Visualização de convergência

Para verificar ainda mais quão bem os resultados correspondem à otimalidade derivada analiticamente, os valores do espaço alvo devem ser convertidos para um segundo alvo $f_{}$A definição original de maximização. Em seguida, desenhe um diagrama de Pareto-front para mostrar até que ponto o algoritmo pode convergir.

from pymoo.util.misc import stack

class MyTestProblem(MyProblem):

    def _calc_pareto_front(self, flatten=True, *args, **kwargs):
        f2 = lambda f1: ((f1/100) ** 0.5 - 1)**2
        F1_a, F1_b = np.linspace(1, 16, 300), np.linspace(36, 81, 300)
        F2_a, F2_b = f2(F1_a), f2(F1_b)

        pf_a = np.column_stack([F1_a, F2_a])
        pf_b = np.column_stack([F1_b, F2_b])

        return stack(pf_a, pf_b, flatten=flatten)

    def _calc_pareto_set(self, *args, **kwargs):
        x1_a = np.linspace(0.1, 0.4, 50)
        x1_b = np.linspace(0.6, 0.9, 50)
        x2 = np.zeros(50)

        a, b = np.column_stack([x1_a, x2]), np.column_stack([x1_b, x2])
        return stack(a,b, flatten=flatten)

problem = MyTestProblem()

A frente de Pareto dos problemas de teste pode ser implementada das seguintes maneiras:

pf_a, pf_b = problem.pareto_front(use_cache=False, flatten=False)
pf = problem.pareto_front(use_cache=False, flatten=True)
plt.figure(figsize=(7, 5))
plt.scatter(F[:, 0], F[:, 1], s=30, facecolors='none', edgecolors='b', label="Solutions")
plt.plot(pf_a[:, 0], pf_a[:, 1], alpha=0.5, linewidth=2.0, color="red", label="Pareto-front")
plt.plot(pf_b[:, 0], pf_b[:, 1], alpha=0.5, linewidth=2.0, color="red")
plt.title("Objective Space")
plt.legend()
plt.show()

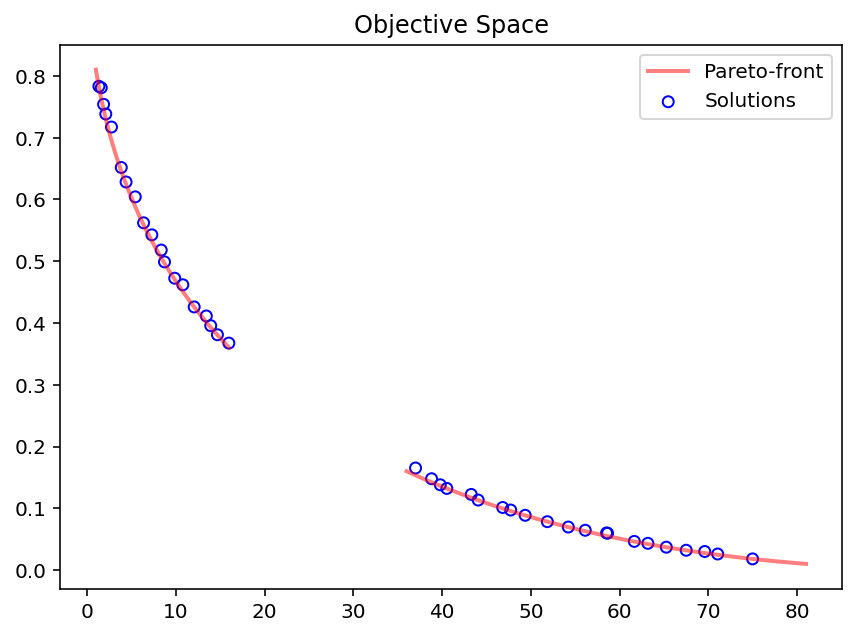
Para desenho de espaço de alta dimensão, consulte:

https://pymoo.org/visualization/index.html

Alternativamente, você pode usar save_history=Truepara verificar a convergência:

from pymoo.optimize import minimize

res = minimize(problem,
               algorithm,
               ("n_gen", 40),
               seed=1,
               save_history=True,
               verbose=False)

X, F = res.opt.get("X", "F")

hist = res.history
print(len(hist)) # 40

n_evals = []             # corresponding number of function evaluations\
hist_F = []              # the objective space values in each generation
hist_cv = []             # constraint violation in each generation
hist_cv_avg = []         # average constraint violation in the whole population

for algo in hist:

    # store the number of function evaluations
    n_evals.append(algo.evaluator.n_eval)

    # retrieve the optimum from the algorithm
    opt = algo.opt

    # store the least contraint violation and the average in each population
    hist_cv.append(opt.get("CV").min())
    hist_cv_avg.append(algo.pop.get("CV").mean())

    # filter out only the feasible and append and objective space values
    feas = np.where(opt.get("feasible"))[0]
    hist_F.append(opt.get("F")[feas])

2) As restrições são satisfeitas

Primeiro, veja quando a primeira solução funcional foi encontrada :

k = np.where(np.array(hist_cv) <= 0.0)[0].min()
print(f"At least one feasible solution in Generation {
      
      k} after {
      
      n_evals[k]} evaluations.")
# At least one feasible solution in Generation 0 after 40 evaluations.

# replace this line by `hist_cv` if you like to analyze the least feasible optimal solution and not the population
vals = hist_cv_avg

k = np.where(np.array(vals) <= 0.0)[0].min()
print(f"Whole population feasible in Generation {
      
      k} after {
      
      n_evals[k]} evaluations.")

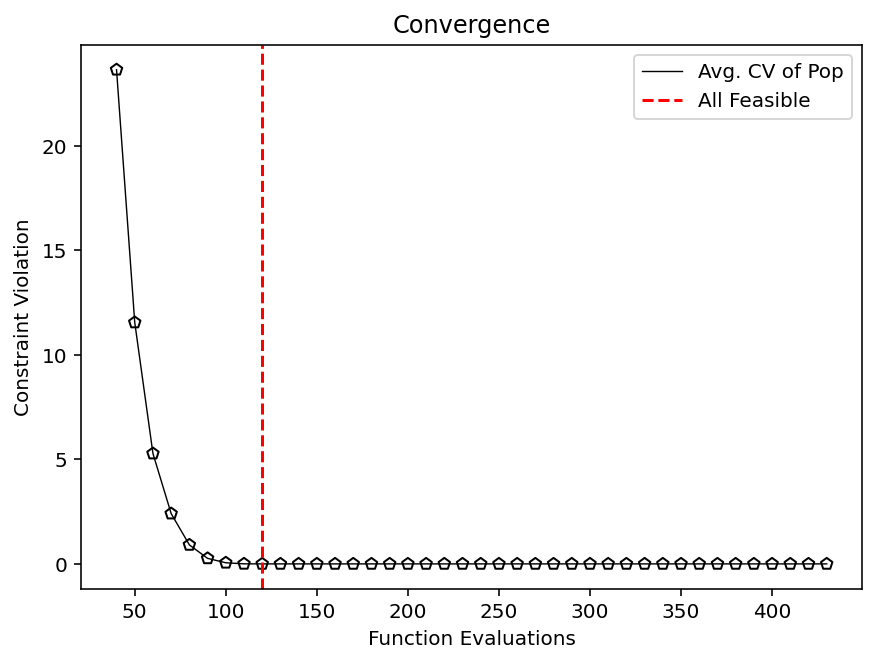
plt.figure(figsize=(7, 5))
plt.plot(n_evals, vals,  color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, vals,  facecolor="none", edgecolor='black', marker="p")
plt.axvline(n_evals[k], color="red", label="All Feasible", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("Constraint Violation")
plt.legend()
plt.show()

# Whole population feasible in Generation 8 after 120 evaluations.

3) Coleção de Pareto desconhecida

Quando a frente de Pareto é desconhecida, é impossível saber se o algoritmo convergiu para o verdadeiro ótimo. Pelo menos nenhuma informação adicional. No entanto, é possível ver quando o algoritmo realizou a maior parte do seu progresso durante o processo de otimização e se o número de iterações deve ser menor ou maior. HypervolumePode ser usado para comparar dois algoritmos.

Hipervolume é um conjunto (conceito) baseado na normalização de limites, utilizado para indicadores de desempenho de problemas multiobjetivos. Cumpre o critério de Pareto e baseia-se na capacidade entre pontos de referência pré-definidos e soluções fornecidas. Portanto, o hipervolume precisa definir um ponto de referência ref_point, que deve ser maior que o valor máximo da frente de Pareto.

# 在多目标优化中，归一化是非常重要的
approx_ideal = F.min(axis=0)
approx_nadir = F.max(axis=0)

from pymoo.indicators.hv import Hypervolume

metric = Hypervolume(ref_point= np.array([1.1, 1.1]),
                     norm_ref_point=False,
                     zero_to_one=True,
                     ideal=approx_ideal,
                     nadir=approx_nadir)

hv = [metric.do(_F) for _F in hist_F]

plt.figure(figsize=(7, 5))
plt.plot(n_evals, hv,  color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, hv,  facecolor="none", edgecolor='black', marker="p")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("Hypervolume")
plt.show()

À medida que o número de dimensões aumenta, o custo computacional do hipervolume aumenta. Ele pode calcular com eficiência o hipervolume preciso para 2 e 3 alvos. Para dimensões superiores, alguns pesquisadores usam o hypervolume approximation, que ainda não está disponível no pymoo.

Um método alternativo de análise de execuções quando a verdadeira frente de Pareto é desconhecida foi proposto recentemente running metric. As métricas de execução mostram as diferenças no espaço alvo entre gerações e visualizam melhorias usando a viabilidade do algoritmo. No pymoo, esta métrica é usada para determinar o término de um algoritmo de otimização multiobjetivo se nenhum critério de encerramento padrão for definido.

Por exemplo, através da análise, verifica-se que o algoritmo foi significativamente melhorado da 4ª para a 5ª geração.

from pymoo.util.running_metric import RunningMetric

running = RunningMetric(delta_gen=5,
                        n_plots=3,
                        only_if_n_plots=True,
                        key_press=False,
                        do_show=True)

for algorithm in res.history[:15]:
    running.notify(algorithm)

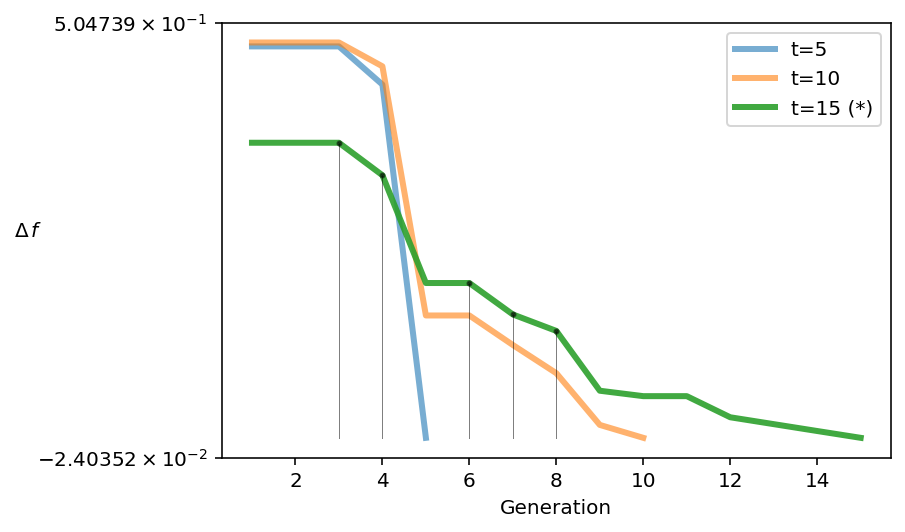
Plote até que a população mostre convergência, com apenas pequenas melhorias aqui:

from pymoo.util.running_metric import RunningMetric

running = RunningMetric(delta_gen=10,
                        n_plots=4,
                        only_if_n_plots=True,
                        key_press=False,
                        do_show=True)

for algorithm in res.history:
    running.notify(algorithm)

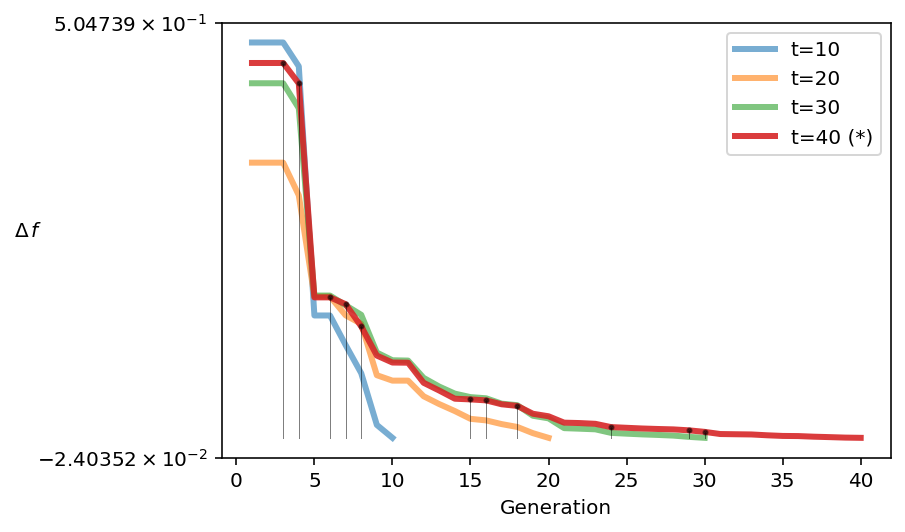
4) O conjunto de Pareto é conhecido ou aproximado

Para problemas reais, devem ser utilizadas aproximações. Executando o algoritmo várias vezes e extraindo soluções não dominadas de todos os conjuntos de soluções , uma solução aproximada pode ser obtida. Se houver apenas uma execução , outra opção é usar o conjunto resultante de soluções não dominadas como aproximação . No entanto, os resultados refletem apenas o progresso do algoritmo na convergência para o conjunto final.

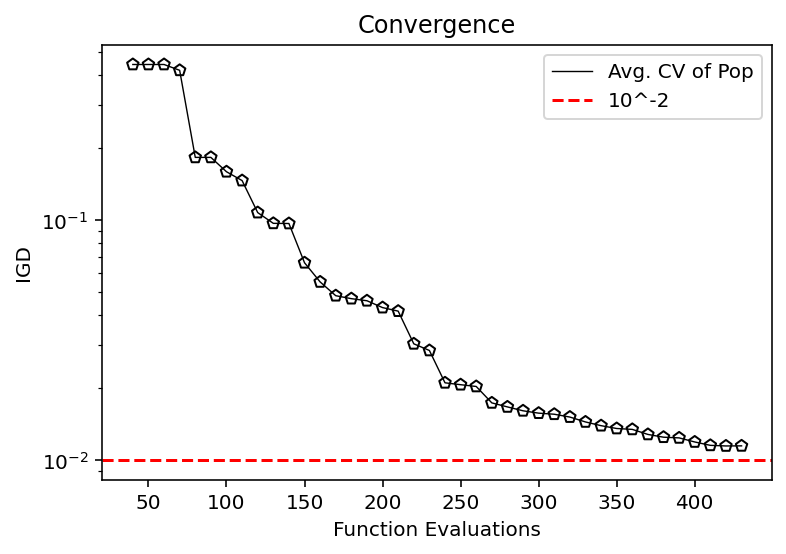
from pymoo.indicators.igd import IGD

metric = IGD(pf, zero_to_one=True)

igd = [metric.do(_F) for _F in hist_F]

plt.plot(n_evals, igd,  color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, igd,  facecolor="none", edgecolor='black', marker="p")
plt.axhline(10**-2, color="red", label="10^-2", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("IGD")
plt.yscale("log")
plt.legend()
plt.show()

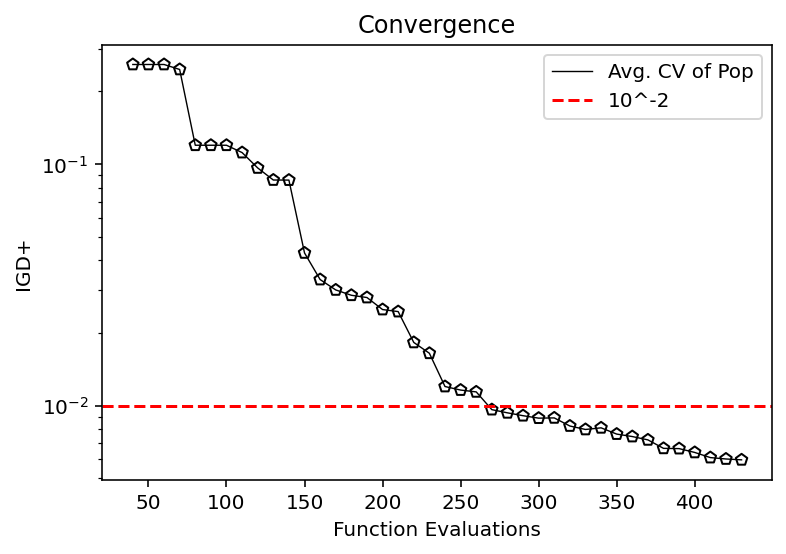
from pymoo.indicators.igd_plus import IGDPlus

metric = IGDPlus(pf, zero_to_one=True)

igd = [metric.do(_F) for _F in hist_F]

plt.plot(n_evals, igd,  color='black', lw=0.7, label="Avg. CV of Pop")
plt.scatter(n_evals, igd,  facecolor="none", edgecolor='black', marker="p")
plt.axhline(10**-2, color="red", label="10^-2", linestyle="--")
plt.title("Convergence")
plt.xlabel("Function Evaluations")
plt.ylabel("IGD+")
plt.yscale("log")
plt.legend()
plt.show()

Para indicadores detalhados, consulte:

https://pymoo.org/misc/indicators.html

referência:

https://pymoo.org/index.html