Índice
【2.1】Conceito de complexidade de tempo
【2.2】 Representação assintótica de Big O
【2.3】Exemplo de cálculo de complexidade de tempo
1. Conceitos básicos
Estrutura de dados : uma coleção de elementos de dados que possuem um ou mais relacionamentos específicos entre si. Logicamente, pode ser dividido em estrutura linear, estrutura hash, estrutura em árvore, estrutura gráfica e assim por diante.
Algoritmo : Uma descrição das etapas para resolver um problema específico. O código é expresso como um conjunto limitado de sequências de instruções para resolver um problema específico.
Complexidade do algoritmo : complexidade de tempo e espaço, que mede a eficiência do algoritmo.Durante a execução do algoritmo, à medida que o tamanho dos dados n aumenta, o tempo e o espaço gastos na execução do algoritmo aumentam.
Complexidade de tempo comum :
| expressão | Notação O grande | equação |
|---|---|---|
| 5201314 | O(1) | ordem constante |
| 3n+4 | Sobre) | ordem linear |
| 3n^2+4n+5 | O(n^2) | ordem quadrada |
| 3log(2)n+4 | O(logn) | Ordem logarítmica |
| 2n+3nlog(2)n+14 | O(nlogn) | Ordem nLogn |
| n^3+2n^2+4n+6 | O (n ^ 3) | ordem cúbica |
| 2^n | O(2^n) | Ordem exponencial |
Relação de complexidade de tempo de algoritmos comuns : O(1) <O(logn) <O(n) <O(nlogn) <O(n^2) <O(2^n) <O(n!) <O(n ^n)
[Comparação de indicadores de complexidade]
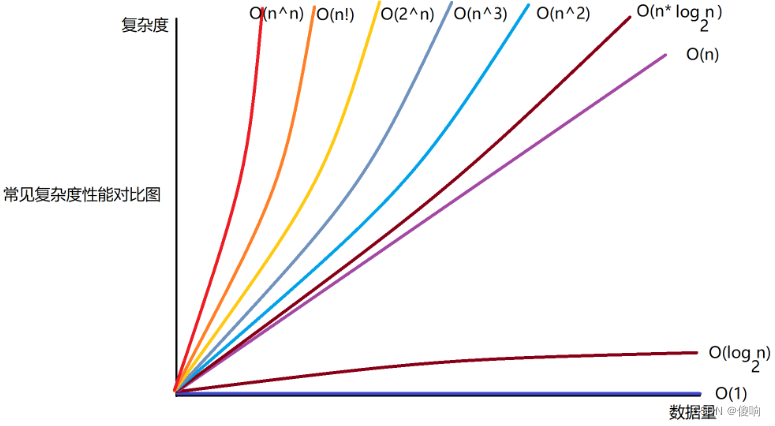
[Complexidade do algoritmo de estrutura de dados criado]
| Grande plano O | Exemplos de aplicação |
|---|---|
| O(1) | Array de acesso aleatório, tabela hash |
| O(logn) | Pesquisa binária, ajuste de heap binário, AVL, pesquisa em árvore vermelha e preta |
| Sobre) | pesquisa linear |
| O(nlogn) | Classificação de heap, classificação rápida, classificação de mesclagem |
| O(n^2) | Classificação por bolha, classificação por seleção, classificação por inserção |
| O(2^n) | árvore de subconjunto |
| Sobre!) | Árvore de arranjo |
2. Complexidade de tempo
【2.1】Conceito de complexidade de tempo
Definição de complexidade de tempo: Na ciência da computação, a complexidade de tempo de um algoritmo é uma função que descreve quantitativamente o tempo de execução do algoritmo. O tempo que leva para executar um algoritmo não pode ser calculado teoricamente, você só pode saber se colocar seu programa na máquina e executá-lo. Mas precisamos testar todos os algoritmos em um computador?
É possível testar tudo em um computador, mas isso é muito problemático, por isso é introduzido o método de análise de complexidade de tempo. O tempo que um algoritmo leva é proporcional ao número de execuções de suas instruções. O número de execuções de operações básicas no algoritmo é a complexidade de tempo do algoritmo.
Ou seja: encontrar a expressão matemática entre uma determinada afirmação básica e o tamanho do problema N é calcular a complexidade de tempo do algoritmo.
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{
int count = 0;
for (int i = 0; i < N; ++i) // 循环次数为N^2
{
for (int j = 0; j < N; ++j)
{
++count;
}
}
for (int i = 0; i < 2 * N; i++) // 循环次数为2 * N
{
++count;
}
int M = 10;
while (M--) // 循环次数为10
{
++count;
}
printf("%d\n", count);
}
// Func1 执行的基本操作次数 :F(N) = (N^2) + (2 * N) + 10
// 比如:N = 10 F(N) = 130
// 比如:N = 100 F(N) = 10210
// 比如:N = 1000 F(N) = 1002010
// 上面N越大后面两项对整个表达式的影响是越来越小的
// 实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
// 最终以大概的次数:上面代码的时间复杂度是N^2【2.2】 Representação assintótica de Big O
Notação Big O : é uma notação matemática usada para descrever o comportamento assintótico de uma função.
[Derivação do método de ordem grande O]
-
Substitua todas as constantes de adição no tempo de execução por uma constante 1. O1 não significa 1 tempo, mas sim um tempo constante.
-
Na função de número de execuções modificada, apenas os termos de ordem mais alta são retidos .
-
Se o termo de ordem mais alta estiver presente e não for 1, remova a constante multiplicada por este termo . O resultado é a ordem Big O.
[Depois de usar a representação assintótica de Big O, a complexidade de tempo de empurrar Func1 é]
// Func1 执行的基本操作次数 :F(N) = (N^2) + (2 * N) + 10
// 比如:N = 10 F(N) = 130
// 比如:N = 100 F(N) = 10210
// 比如:N = 1000 F(N) = 1002010
// 结果:去掉(2*N)去掉(10) -> 时间复杂度是N^2Pelo exposto, descobriremos que a representação assintótica do Big O remove itens que têm pouco impacto nos resultados e expressa o número de execuções de forma concisa e clara.Além disso, a complexidade de tempo de alguns algoritmos tem o melhor, o médio e o pior. casos:
-
Pior caso : número máximo de execuções (limite superior) para qualquer tamanho de entrada.
-
Caso médio : o número esperado de execuções para qualquer tamanho de entrada.
-
Melhor caso : número mínimo de execuções (limite inferior) para qualquer tamanho de entrada.
-
Por exemplo : Pesquise um dado x em uma matriz de comprimento N.
-
Melhor caso : encontrado 1 vez.
-
Pior caso : encontrado N vezes.
-
Situação média : N/2 vezes encontrada.
Na prática, a preocupação geral é o pior caso de operação do algoritmo!
【2.3】Exemplo de cálculo de complexidade de tempo
【Exemplo】
// 计算Func2的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)// 循环次数:2 * N
{
++count;
}
int M = 10;
while (M--) // // 循环次数:10
{
++count;
}
printf("%d\n", count);
}
// 正常为:(2 * N) + 10
// 在此:10 影响不大, 2为固定值影响不大,影响时间复杂度的是N
// 以大O表示法:O(N)【Exemplo】
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k) // 循环次数为:M次
{
++count;
}
for (int k = 0; k < N; ++k) // 循环次数为:N次
{
++count;
}
printf("%d\n", count);
}
// 正常为:M + N
// 在此:M 和 N 的准确值都是不知道的,所以都算在时间复杂度成员里
// 以大O表示法:O(M + N)【Exemplo】
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k) // 循环次数为:100次
{
++count;
}
printf("%d\n", count);
}
// 正常为:100次
// 在此:N 没有参与任何东西
// 以大O表示法:O(1)【Exemplo】
// 计算strchr的时间复杂度?
const char * strchr(const char * str, int character); // O(N)【Exemplo】
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end) // 循环次数为:等差数列
{ // N-1 N-2 N-3 N-4.... -> 1+2+3+N-1 = N(N-1)/2
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}
// 正常为:
// 在此:实例5基本操作执行最好N次,最坏执行了(N*(N+1)/2次,通过推导大O阶方法+时间复杂度一般看最坏,时间复杂度为 O(N ^ 2)
// 以大O表示法:O(N^2)这是最坏的情况加
// 最好的情况下是O(N)【Exemplo】
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x) // O(N * Log(2)n)
{
assert(a);
int begin = 0;
int end = n - 1;
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}【Exemplo】
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N) // O(N)
{
if (0 == N)
return 1;
return Fac(N - 1)*N;
}【Exemplo】
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N) // O(2^N) -> 斐波那契数相当于是一个很垃圾的算法
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}
// 优化
long long Fac(size_t N)
{
if (N < 3)
return 1;
long long f1 = 1, f2 = 1, f3;
for (size_t i = 3; i <= N; i++)
{
f3 = f1 + f2;
// 迭代
f1 = f2;
f2 = f3;
}
return f3;
}3. Complexidade espacial
A complexidade do espaço também é uma expressão matemática, que é uma medida da quantidade de espaço de armazenamento que um algoritmo ocupa temporariamente durante a operação .
A complexidade do espaço não é quantos bytes de espaço o programa ocupa, porque isso não é muito significativo, então a complexidade do espaço é calculada pelo número de variáveis. As regras de cálculo da complexidade espacial são basicamente semelhantes à complexidade prática, e a notação assintótica O grande também é usada .
Nota: O espaço de pilha necessário quando a função está em execução (armazenamento de parâmetros, variáveis locais, algumas informações de registro, etc.) foi determinado durante a compilação, portanto, a complexidade do espaço é determinada principalmente pelo espaço adicional explicitamente aplicado pela função em tempo de execução .
【Exemplo】
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n) // 常数个额外空间,所以空间复杂度为 O(1)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}【Exemplo】
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n) // 动态开辟了N个空间,空间复杂度为 O(N)
{
if (n == 0)
{
return NULL;
}
long long * fibArray = (long long *)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}【Exemplo】
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N) // 递归调用了N次,开辟了N个栈帧,每个栈帧使用了常数个空间。空间复杂度为O(N)
{
if (N == 0)
return 1;
return Fac(N - 1) * N;
}