Diretório de artigos
1. Método de interpolação linear
1.1 Interpolação do vizinho mais próximo

A imagem acima é um diagrama esquemático da interpolação unidimensional do vizinho mais próximo. Os pontos xi-1, xi, xi+1 no eixo de coordenadas são divididos em dois pares e meio de intervalos iguais (divididos pela linha pontilhada vermelha), de modo que cada ponto de coordenada no não-limite tenha uma vizinhança de largura igual e, de acordo com o valor de cada ponto de coordenada, uma restrição de função semelhante a uma função por partes é formada, de modo que o valor de cada ponto de coordenada interpolado seja igual a o valor do ponto de coordenada original na vizinhança. Por exemplo, se o ponto de interpolação x está localizado na vizinhança do ponto de coordenada xi, então seu valor f(x) é igual a f(xi).

A imagem acima é um diagrama quantitativo de visualização superior da interpolação bidimensional do vizinho mais próximo. (x0, y0), (x0, y1), (x1, y0), (x1, y1) são pontos de coordenadas na imagem original e o valores de cinza são respectivamente correspondentes a Q11, Q12, Q21, Q22. O ponto de interpolação (x, y) cujo valor de cinza é desconhecido, de acordo com as restrições do método de interpolação do vizinho mais próximo, é o mais próximo do ponto de coordenada (x0, y0) (ou seja, está localizado na vizinhança de (x0, y0)), então o ponto de interpolação O valor cinza de (x, y) P = Q11.
1.2 Interpolação Linear

A figura acima é um diagrama esquemático qualitativo de interpolação linear unidimensional. Os valores de cada ponto xi-1, xi, xi+1 ... no eixo de coordenadas são "conectados diretamente em pares" como segmentos de linha, portanto formando uma função de restrição contínua. Para um ponto de coordenada de interpolação como x, seu valor deve ser f(x) de acordo com a função de restrição. Como a curva da função de restrição entre cada dois pontos de coordenadas é um segmento de linha linear, ela é "linear" para o resultado da interpolação, portanto, esse método é chamado de interpolação linear.

A figura acima é um diagrama esquemático quantitativo de interpolação linear unidimensional, onde x0 e x1 são os pontos de coordenadas originais, e os valores de cinza correspondem a y0 e y1 respectivamente. Para o ponto de interpolação x cujo valor de cinza é desconhecido, de acordo com as restrições do método de interpolação linear, na função linear composta por (x0, y0) e (x1, y1), seu valor de cinza y é: y = y 0 + ( x
− x 0 ) y 1 − y 0 x 1 − x 0 = y 0 + ( x − x 0 ) y 1 − ( x − x 0 ) y 0 x 1 − x 0 y=y_0+\left(x- x_0\direita ) \frac{y_1-y_0}{x_1-x_0}=y_0+\frac{\left(x-x_0\right) y_1-\left(x-x_0\right) y_0}{x_1-x_0}y=y0+( x−x0)x1−x0y1−y0=y0+x1−x0( x−x0)y1−( x−x0)y0
1.3 Algoritmo de Interpolação Bilinear (Interpolação Bilinear)

É fácil expandir da interpolação linear unidimensional para a interpolação bilinear de imagens bidimensionais. Cada vez, três interpolações lineares de primeira ordem são necessárias para obter o resultado final. A figura acima mostra um diagrama de estrabismo qualitativo do processo. Entre eles, (x0, y0), (x0, y1), (x1, y0), (x1, y1) são pontos de coordenadas de pixel na imagem original, e os valores de cinza correspondem a f(x0, y0), f(x0, y1), f(x1, y0), f(x1, y1). Para o ponto de interpolação (x, y) cujo valor de cinza é desconhecido, de acordo com as restrições do método de interpolação bilinear, pode ser obtido por interpolação linear unidimensional dos pontos de coordenadas de pixel (x0, y0) e (x0, y1 ) no eixo y. f(x0, y), a partir dos pontos de coordenadas de pixel (x1, y0) e (x1, y1) faça interpolação linear unidimensional no eixo y para obter f(x1, y) e depois de (x0, y) e (x1 , y) Execute a interpolação linear unidimensional no eixo x para obter o valor cinza f(x, y) do ponto de interpolação (x, y). Obviamente, se a interpolação linear unidimensional for realizada primeiro no eixo x e depois no eixo y, os resultados obtidos são exatamente os mesmos, apenas a diferença está em ordem . Há alterações, mas não afetadas), vamos

mudar a ordem. Em primeiro lugar, f(x, y0) é obtido por interpolação linear unidimensional a partir dos pontos de coordenadas de pixel (x0, y0) e (x1, y0) no eixo x, e f(x, y0) é obtido a partir da coordenada de pixel pontos (x0, y1) e (x1, y1) em x Execute a interpolação linear unidimensional na direção axial para obter f(x, y1):
f ( x , y 0 ) = x 1 − xx 1 − x 0 f ( x 0 , y 0 ) + x − x 0 x 1 − x 0 f ( x 1 , y 0 ) f ( x , y 1 ) = x 1 − xx 1 − x 0 f ( x 0 , y 1 ) + x − x 0 x 1 − x 0 f ( x 1 , y 1 ) \begin{alinhado} &f\left(x, y_0\right)= \frac{x_1-x}{x_1-x_0} f\esquerda(x_0, y_0\direita)+\frac{x-x_0}{x_1-x_0} f\esquerda(x_1, y_0\direita)\\ &f\esquerda (x, y_1\direita)=\frac{x_1-x}{x_1-x_0} f\esquerda(x_0, y_1\direita)+\frac{x-x_0}{x_1-x_0} f\esquerda(x_1, y_1 \direita) \end{alinhado}f( x ,y0)=x1−x0x1−xf( x0,y0)+x1−x0x−x0f( x1,y0)f( x ,y1)=x1−x0x1−xf( x0,y1)+x1−x0x−x0f( x1,y1)
Em seguida, execute a interpolação linear unidimensional no eixo y de (x, y0) e (x, y1) para obter o valor cinza f(x, y) do ponto de interpolação (x, y):
f ( x , y ) = y 1 − yy 1 − y 0 f ( x , y 0 ) + y − y 0 y 1 − y 0 f ( x , y 1 ) f(x, y)=\frac{y_1 -y}{y_1-y_0} f\esquerda(x, y_0\direita)+\frac{y-y_0}{y_1-y_0} f\esquerda(x, y_1\direita)f ( x ,y )=y1−y0y1−vocêf( x ,y0)+y1−y0y−y0f( x ,y1)
f ( x , y ) = ( y 1 − y ) ( x 1 − x ) ( y 1 − y 0 )
( x 1 − x 0 ) f ( x 0 , y 0 ) + ( y 1 − y ) ( x − x 0 ) ( y 1 − y 0 ) ( x 1 − x 0 ) f ( x 1 , y 0 ) + ( y − y 0 ) ( x 1 − x ) ( y 1 − y 0 ) ( x 1 − x 0 ) f ( x 0 , y 1 ) + ( y − y 0 ) ( x − x 0 ) ( y 1 − y 0 ) ( x 1 − x 0 ) f(x, y)=\frac{\esquerda(y_1-y\direita)\esquerda(x_1-x\direita)}{\esquerda(y_1-y_0\direita)\esquerda(x_1-x_0\direita)} f\esquerda(x_0, y_0\direita)+\frac{\esquerda(y_1-y\direita)\esquerda(x-x_0\direita)}{\esquerda(y_1-y_0\direita)\esquerda(x_1-x_0\ direita)} f\esquerda(x_1, y_0\direita)+\frac{\esquerda(y-y_0\direita)\esquerda(x_1-x\direita)}{\esquerda(y_1-y_0\direita)\esquerda(x_1 -x_0\direita)} f\esquerda(x_0, y_1\direita)+\frac{\esquerda(y-y_0\direita)\esquerda(x-x_0\direita)}{\esquerda(y_1-y_0\direita)\ esquerda(x_1-x_0\direita)}f ( x ,y )=( y1−y0)( x1−x0)( y1−y )( x1−x )f( x0,y0)+( y1−y0)( x1−x0)( y1−y )( x−x0)f( x1,y0)+( y1−y0)( x1−x0)( y−y0)( x1−x )f( x0,y1)+( y1−y0)( x1−x0)( y−y0)( x−x0)
1.4 Interpolação Bicúbica
Também conhecida como interpolação de convolução cúbica/interpolação bicúbica, em análise numérica, a interpolação bicúbica é o método de interpolação mais comumente usado no espaço bidimensional. Neste método, o valor de pixel cinza f(x, y) do ponto de interpolação (x, y) é obtido pela média ponderada dos dezesseis pontos de amostragem mais próximos na grade retangular, e o peso de cada ponto de amostragem é determinado por o ponto A distância até o ponto a ser interpolado é determinada, e esta distância inclui a distância nas direções horizontal e vertical. Em contraste, a interpolação bilinear é ponderada pelos quatro pontos de amostragem circundantes.

A figura acima é um diagrama esquemático de uma vista superior de interpolação bicúbica de uma imagem bidimensional. Suponha que as coordenadas do ponto de interpolação a serem calculadas sejam (i+u, j+v), e os valores de cinza dos 16 pontos de coordenadas de pixel (grid) em torno dele sejam conhecidos, e os respectivos pesos dos 16 pontos precisam a ser calculado. Tome o ponto de coordenada do pixel (i, j) como exemplo, porque a distância entre este ponto e o ponto de interpolação (i+u, j+v) nas direções do eixo y e do eixo x é u e v respectivamente, então o peso é w (u) × w(v), onde w( ) é o kernel do peso de interpolação (que pode ser entendido como a função de peso definida). Da mesma forma, podem ser obtidos os respectivos pesos dos pontos de coordenadas restantes de 15 pixels. Então, o valor cinza f(i+u, j+v) do ponto de interpolação (i+u, j+v) a ser calculado será obtido pelo seguinte cálculo: f ( i + u , j + v ) = A × B
× C f(i+u, j+v)=A \vezes B \vezes Cf ( eu+você ,j+v )=A×B×C
onde cada item é representado por um vetor ou matriz como:
A = [ w ( 1 + u ) w ( u ) w ( 1 − u ) w ( 2 − u ) ] B = [ f ( i − 1 , j − 1 ) f ( i − 1 , j + 0 ) f ( i − 1 , j + 1 ) f ( i − 1 , j + 2 ) f ( i + 0 , j − 1 ) f ( i + 0 , j + 0 ) f ( i + 0 , j + 1 ) f ( i + 0 , j + 2 ) f ( i + 1 , j − 1 ) f ( i + 1 , j + 0 ) f ( i + 1 , j + 1 ) f ( i + 1 , j + 2 ) f ( i + 2 , j − 1 ) f ( i + 2 , j + 0 ) f ( i + 2 , j + 1 ) f ( i + 2 , j + 2 ) ] C = [ w ( 1 + v ) w ( v ) w ( 1 − v ) w ( 2 − v ) ] T \begin{reunido} \mathrm{A}=\left[\begin{array}{llll} w(1+u) & w(u) & w(1-u) & w(2-u) \end{array}\right] \\ \mathrm{B}=\left[\begin{array}{llll} f(i-1, j-1 ) & f(i-1, j+0) & f(i-1, j+1) & f(i-1, j+2) \\ f(i+0, j-1) & f(i +0, j+0) & f(i+0, j+1) & f(i+0, j+2) \\ f(i+1, j-1) & f(i+1, j+ 0) & f(i+1, j+1) & f(i+1, j+2) \\ f(i+2, j-1) & f(i+2, j+0) & f( i+2, j+1) & f(i+2,j+2) \end{array}\right]\\\mathrm{C}=\left[\begin{array}{llll} w(1+v) & w(v) & w(1-v) & w(2-v) \end{array}\right]^T\end{recolhidos}A=[w ( 1+você )vc ( u )w ( 1−você )w ( 2−você )]B=
f ( eu−1 ,j−1 )f ( eu+0 ,j−1 )f ( eu+1 ,j−1 )f ( eu+2 ,j−1 )f ( eu−1 ,j+0 )f ( eu+0 ,j+0 )f ( eu+1 ,j+0 )f ( eu+2 ,j+0 )f ( eu−1 ,j+1 )f ( eu+0 ,j+1 )f ( eu+1 ,j+1 )f ( eu+2 ,j+1 )f ( eu−1 ,j+2 )f ( eu+0 ,j+2 )f ( eu+1 ,j+2 )f ( eu+2 ,j+2 )
C=[w ( 1+v )w ( v )w ( 1−v )w ( 2−v )]T
插值权重核 w(·) 为BiCubic函数:
w ( x ) = { 1 − 2 ∣ x ∣ 2 + ∣ x ∣ 3 , ∣ x ∣ < 1 4 − 8 ∣ x ∣ + 5 ∣ x ∣ 2 − ∣ x ∣ 3 , 1 ≤ ∣ x ∣ < 2 0 ∣ x ∣ ≥ 2 w(x)=\left\{\begin{array}{cc} 1-2|x|^2+|x|^3 & ,|x| <1 \\ 4-8|x|+5|x|^2-|x|^3, & 1 \leq|x|<2 \\ 0 & |x| \geq 2 \end{array}\right.w ( x )=⎩
⎨
⎧1−2∣ x ∣2+∣ x ∣34−8∣ x ∣+5∣ x ∣2−∣ x ∣3 ,0,∣ x ∣<11≤∣ x ∣<2∣ x ∣≥2
Sua imagem de função é a seguinte:

2. Aprendizado Profundo
2.1 Deconvolução/Convolução Transposta (Deconvolução/Convolução Transposta)
Para obter detalhes, consulte: Operações de convolução em aprendizado profundo
A figura a seguir mostra um kernel de convolução 2x2 e uma convolução transposta quando stride=1.

O tensor kernel é multiplicado elemento por elemento com o tensor de entrada e colocado no local correspondente. Ou seja, o primeiro elemento é 0, ou seja, 0 é multiplicado por todo o tensor nuclear e colocado na posição correspondente. O segundo elemento é 1, que é multiplicado pelo tensor kernel e colocado no slide correspondente à próxima posição. e assim por diante. Quatro gráficos são obtidos e a saída final é obtida adicionando os quatro gráficos. O passo de exemplo aqui é 1, então o passo deslizante é 1.
A fórmula resumida é:
Y [ i : i + h , j : j + w ] + = X [ i , j ] ∗ K \mathrm{Y}[\mathrm{i}: \mathrm{i}+\mathrm {h}, \mathrm{j}: \mathrm{j}+\mathrm{w}]+=\mathrm{X}[\mathrm{i}, \mathrm{j}] * \mathrm{~K}S [ eu:eu+h ,j:j+w ] +=X [ eu ,j ]∗ K
onde o tamanho de Y é o tamanho da convolução e a fórmula de cálculo é invertida:
Convolução:out = ( Input − kernel + 2 ∗ padding ) / stride + 1 out = (Input - kernel + 2*padding) / stride +1fora _ _=( eu coloquei _ _ _−k er n e l+2∗p a d d in g ) / s r i d e+1
反卷积:out = ( I nput − 1 ) ∗ stride + kernel − 2 ∗ padding out = (Input - 1) * stride + kernel - 2*paddingfora _ _=( eu coloquei _ _ _−1 )∗passo _ _ _ _ _+k er n e l−2∗p adicionar em g _
-
Stride
Stride é o passo deslizante.
A figura abaixo é um kernel de convolução 2x2, convolução transposta quando stride=2.

-
O preenchimento
é diferente da convolução regular, onde o preenchimento é aplicado à saída na convolução transposta (a convolução regular aplica o preenchimento à entrada). Por exemplo, quando o número de preenchimento em ambos os lados da altura e largura é especificado como 1, a primeira e a última linha e coluna serão removidas da saída da convolução transposta.
2.2 Unpooling
Anti-pooling é a operação inversa do pooling. De um modo geral, existem três métodos de anti-pooling
-
O vizinho mais próximo é copiar os mesmos dados quatro vezes para obter o efeito de ampliação de quatro vezes. Esse método também é chamado de agrupamento anti-média.

-
Bed of Nails
coloca os dados no canto superior esquerdo da posição correspondente e preenche o restante com 0

-
MaxUnpooling
requer o registro da posição da coordenada do valor máximo de ativação durante o processo de pooling e, em seguida, a restauração do tamanho original. Durante o unpooling, apenas as coordenadas da posição do valor máximo de ativação durante o processo de pooling são ativadas e os outros valores são definidos como 0. Claro, este processo é apenas uma aproximação. Porque no processo de pooling, exceto para a posição do valor máximo, os outros valores não são todos 0.

2.3 Convolução de subpixel (PixelShuffle)
A ESPCN propôs o algoritmo PixelShuffle pela primeira vez. Para obter detalhes, consulte: Algoritmo de super-resolução ESPCN: "Real-Time Single Image and Video Super-Resolution Using an Efficient Sub-Pixel"
A ideia central da convolução de subpixel:一张图像放大r倍,就相当于每个像素都放大r倍。
O processo de convolução da penúltima camada da rede 输出通道数é a imagem característica da r^2imagem original e então organizada periodicamente através da camada de sub-pixel de convolução para obter uma imagem reconstruída com um tamanho de .同样大小(w × r , h × r)
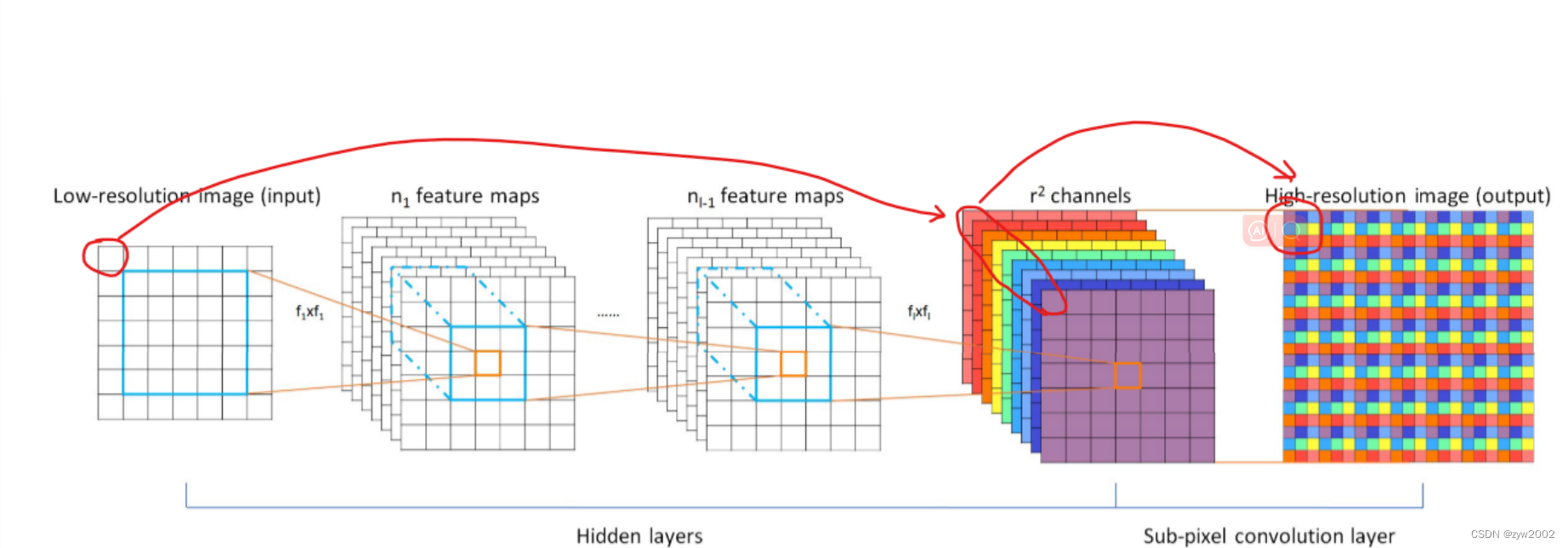
Como mostrado na figura acima, as 9 feições emolduradas pelo círculo vermelho na penúltima camada são dispostas para formar a pequena caixa na última camada apontada pela seta. Este é o bloco de reconstrução formado pelos pixels enquadrados na imagem original através a rede. Esses nove pixels apenas triplicam o comprimento e a largura do pixel original.
A convolução subpixel (convolução subpixel) na verdade não possui uma operação de convolução, mas simplesmente extrai recursos e os organiza de maneira simples.
3. Aplicação em SR
Vários métodos de upsampling em tarefas de super-resolução:
- A interpolação bicúbica é usada como base e as camadas convolucionais são usadas para correção de ajuste fino. DCSCN
- A camada de deconvolução usa pangding para expandir a imagem. SRDenseNet
- Use um tamanho de passo de 1 r \frac{1}{r}r1A deconvolução da ampliação da imagem. FSRCNN
- A convolução de subpixel, uma camada de convolução implícita que não requer computação adicional, constrói a saída reorganizando. ESPCN
4. Referência
[1] [Processamento de imagem] Explicação detalhada da interpolação do vizinho mais próximo, interpolação linear, interpolação bilinear, interpolação bicúbica
[2] Resumo dos métodos de upsampling (interpolação e aprendizado profundo)