SP5971 LCMSUM-LCM Soma (função de Euler, derivação da fórmula)

SP5971 LCMSUM - Soma LCM

Quer dizer: pergunte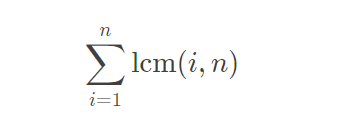

Empurrador

$$\begin{gathered} \sum _{i=1}^{n}lcm(i,n) \\ \sum _{i=1}^n\frac{in}{gcd(i,n)} \\ n\sum _{i=1}^n\frac{Eu}{gcd(i,n)} \\ n\underset{d|n}{\Sigma }\sum _{i=1}^n\frac{Eu}{d}\left[gcd\right(i,n)=d] \\ n\underset{d|n}{\Sigma }\sum _{i=1}^{\frac{n}{d}}i\left[gcd\right(i,\frac{n}{d})=1] \\ n\underset{d|n}{\Sigma }\frac{\left(\varphi \right(d)+[d=1\left]\right)\times d}{2} \end{gathered}$$

A primeira fórmula é o problema; a
segunda fórmula é colocar $lcm\; é$ desmontado; a
terceira fórmula é eliminar a constante n; a
quarta fórmula é enumerar todos os fatores de n, que podem ser transformados na quarta fórmula; a
quinta fórmula é ad de$\left[\right[gcd(i,n)=d]$ Proponha dentro e selecione a faixa de valores, número enumerado$\frac{Eu}{d}$Transformação $i$和$\left[gcd\right(i,n)=d]$ torna-se$\left[gcd\right(i,\frac{n}{d})=1]$ ; A
sexta fórmula é usar uma propriedade da função de Euler:$ComoseGCD(I,n)=1,entãogcd(n-eu,n)=1(i\ne 1)$ , e então pode ser transformado na sexta fórmula;
fim

$Code$

#include<bits/stdc++.h>
using namespace std;
const int N = 1e6+10;
typedef long long ll;
ll st[N], p[N], phi[N], sum[N], ans[N], tot;
//phi：欧拉函数，sum函数第六个公式中的欧拉函数phi*d，ans是存放答案的数组；
void init() {
    
    
    phi[1] = 1, st[1] = 1, sum[1] = 1;//sum[1]=1,把d=1的情况考虑了进去
    for(int i=2; i<N; i++) {
    
    
        if(!st[i]) p[tot++] = i, phi[i] = i-1, sum[i] = 1ll*phi[i]*i/2;
        for(int j=0; j<tot&&i*p[j]<N; j++) {
    
    
            st[i*p[j]] = 1;
            if(i % p[j] == 0) {
    
    
                phi[i*p[j]] = phi[i]*p[j];
                sum[i*p[j]] = 1ll*phi[i*p[j]]*(i*p[j])/2; 
                break;
            }
            phi[i*p[j]] = phi[i]*(p[j]-1);
            sum[i*p[j]] = 1ll*phi[i*p[j]]*(i*p[j])/2; 
        }
    }
    //类埃氏筛，把n的全部因子d加起来ans[n]+=sum[d];
    for(int i=1; i<N; i++) {
    
    
        for(int j=i; j<N; j+=i)
        ans[j] += sum[i];
    }
}
inline ll read() {
    
    //快读
    ll x = 0, f = 1; char c = getchar();
    while(c < '0' || c > '9') {
    
    
        if(c == '-') f = -1;
        c = getchar();
    }
    while(c >= '0' && c <= '9') {
    
    
        x = (x << 1) + (x << 3) + (c ^ 48);
        c = getchar();
    }
    return x * f;
}

int main() {
    
    
    init();//初始化
    ll t;
    t = read();
    while(t--) {
    
    
        int n;
        n = read();
        printf("%lld\n", ans[n]*n);
    }
    return 0;
}

Fim