人々は、反復を行う行うには、神を再帰的。
反復するために再帰する人間、である
神。 人々は、彼らがある程度に達するといないという理由だけで、再帰の深さの、唯一の神は再帰を理解することができると言う傾向にあります。人間の脳は本当に想像することはできませんが、再帰は神の視点からの問題のようなものを意味し、問題、考えるトップダウン方法があるにもあるため。
今日はフィボナッチによって理解し、nの数の発見のための方法の種類
どのように正確に書かれたコードは
何の方法によって最適化されていますか?
最初のソリューション:再帰的なソリューション
#include <cstdio>
#include <iostream>
//输入的n为正整数
int fibonacci(int n) {
//若未到达递归基,递归求解前两项
if (n > 2 ) {
return fibonacci(n - 1) + fibonacci(n - 2);
}
//递归结束条件,到达基返回f(1),f(2)的值
if (n == 2 || n == 1) {
return n - 1;
}
}
//测试
int main() {
int n;
std::cin >> n;
int result = fibonacci(n);
std::cout << result;
}
これは私の個人的な書き込みよりも多くあり
、実際にして、三項演算子によるプログラムを合理化することができます:
#include <cstdio>
#include <iostream>
//输入的n为正整数
//骚操作:三目运算符
int fib(int n) {return (n < 3) ? n - 1 : fib(n - 1) + fib(n- 2);}
//测试
int main() {
int n;
std::cin >> n;
int result = fib(n);
std::cout << result;
}
我々は機能時間の複雑さを求める:
T(1)= T(2)= 1、(N-ステップのみO(1)の答え1,2)。
T(N)= T(N -1)+ T(N-2)+ 1(N> 2、再帰的に、各テイクT(N-1)と時刻T(N-2)回そして二段階動作時間O(1)の添加
の順序:
S(N)=を[T(N)+ 1/2、
発見S =フィボナッチ(2)、(1)
S(2)=フィボナッチ( 3)
S(3)=フィボナッチ(4)= S(2)+ S(1)
その結果S(N)=フィボナッチ(N + 1)= S(N-1)+ S(N-2)
リリースT( N-)= 2 * S(。。。N-) -フィボナッチ1 = 2 *(N + 1) - 1
= O(fibnacci(N + 1))
以下で示されるフィボナッチリース期間の式ので:
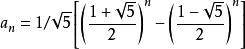
それの時間複雑にほぼ等しいO(2 ^ n)を
使用すると、とき項目45、コンピュータはカトンを開始し、ほぼ1秒のため、などの項目66に、カウントするようにしたい場合は、指数関数的複雑さ、おそらく一日待たなければなりません。
第二の溶液:ニーモニック再帰の最適化
この方法は、依然としてフィボナッチ再帰、各再帰的であるが、得られた値は、n個のデータセットの合計であるF必要がそれを使用するときに呼び出される[n]の配列を、維持するために、格納され、 nは、その後、私たちはグループを呼び出します。
#include<iostream>
#include<cstring>
using namespace std;
int f[10000000];
int DFS(int n)
{
if(f[n])
return f[n];
else
{
f[n]=DFS(n-1)+DFS(n-2);
return f[n];
}
}
int main()
{
memset(f,0,sizeof(f));
f[1]=1;
f[2]=1;
int n;
cin>>n;
DFS(n);
cout<<DFS(n)<<endl;
return 0;
この方法は、複雑さがに還元される時間であり、O(n)は、空間複雑さはO(N)に達したので、我々は、N個のストレージグループのアレイを使用します。
第三ソリューション:動的プログラミングの最適化が続きます
小さなファン弟小平の教師として
、彼はクラスで言及していた有名なが言っていた
メイクIT業務、
IT、右メイク
。メイクIT FAST
:問題の当社のソリューション
、まず、我々はそれが正常に実行してみましょうが
、我々はそれをバグをさせない、
そして最終的に我々はそれを聞かせて速く走ります。
私たちは、最初の問題を解決すると、トップダウン再帰関数呼び出しで、そう、遅い速度を生じる可能性がある状況への呼び出しが繰り返されます。
我々は再帰を記録した二回目は、繰り返し呼び出しの問題を解決しますが、スペースは、オーバーヘッド、したがって、それが大きくなっています。
そして第三に、我々は問題を解決するために、動的なプログラミングのアイデアを使用しています。
ダイナミックプログラミング
(1)最適な下部構造は:最適解を意味するそのサブ問題を含む最適なソリューションです。
(2)重複サブ問題:重複サブ問題は、動的プログラミングを使用するための必要条件ではないが、より完全であるダイナミックプログラミングの利点を実証することができ、問題の性質を重複問題の子があります。
寸法(3)動的プログラミング:質問再帰式のフィボナッチ数は一つだけ変数iを伴い、それは一次元の動的プログラミングです。
(4)状態遷移方程式:
2つの動的プログラミングソリューションがあります。
トップダウンソリューション1.メモ(実際には、第二の溶液は、あまりにも、動的プログラミングのアイデアです)
2.ボトムアップではなく、繰り返し呼び出しインスタンス、これを問題を解決するためにこの方法は、一般的に反復することによって達成されます。
以下の図は、数学モデリング問題我々の出会いは、一般的に確立される:
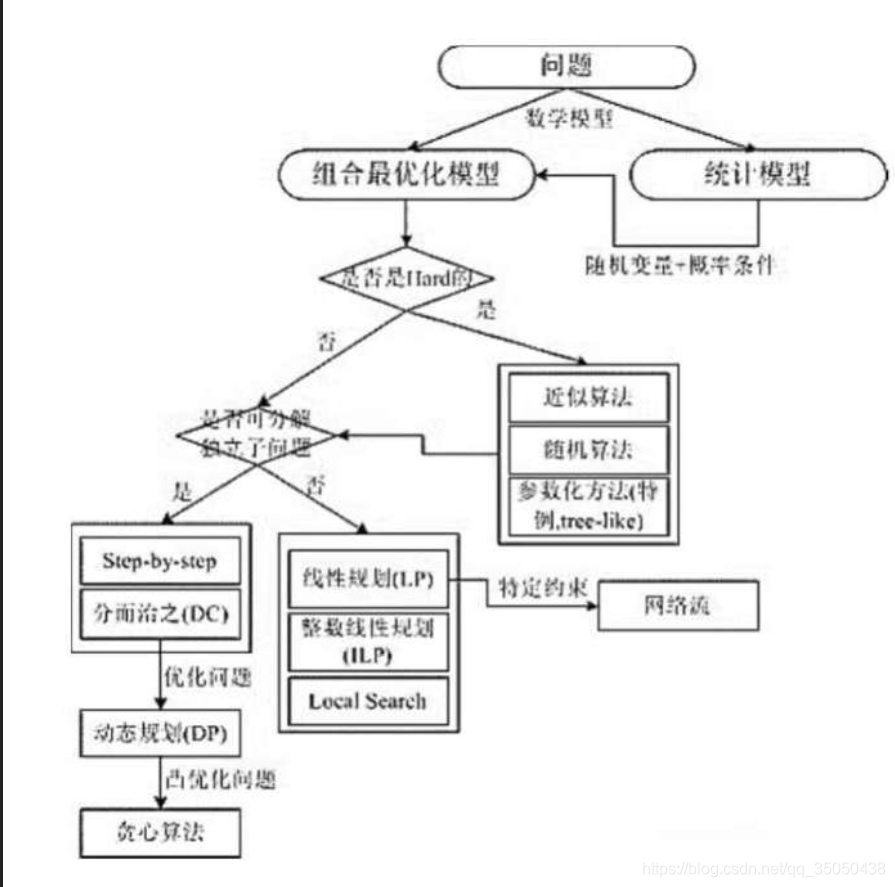
数のフィボナッチ状態遷移方程式は、
F(N)= F(N - 1)+ F(N - 2)
我々は、唯一の解決の現在の状態を見つけます次のように最初の二つと、現在の状態の最初の二つの記録のため、限り、各コードが計算されます。
#include <cstdio>
#include <iostream>
int fibonacci(int n)
{
if (n <= 2)
return n-1;
int first = 0, second = 1, result;
for (int i = 3; i <= n; i++)
{
//利用当前已知的两个值去求解下一个值,并更新当前两个值
result = first + second;
first = second;
second = result;
}
return result;
}
//测试
int main() {
int n;
std::cin >> n;
int result = fibonacci(n);
std::cout << result;
}
この時点で、我々は唯一の問題を解決するために循環させるために使用するだけでなく、O(n)のラインレベルの成長に複雑ダウン。
スペースのみO(1)レベルを使用していると、それは素晴らしいことです!
第4の解決:高速電力解決行列
高速電力:消費電力の結果を得るために、迅速なアプローチ
当我们计算21000的时候,我们计算机会将1000个2相乘得到结果,计算1000次。
因此我们用指数快速幂的方式,进行计算,指数快速幂是将指数变为二进制,通过二的次方来加快计算。
例:431常规做法要计算31次4的乘积。计算乘次数31次
矩阵快速幂将31转换为二进制即:11111:24 +23 +22 +21+20计算次数10次。
但显然:快速幂是对幂计算的较好的优化,但不一定是最好的优化。
显然我们这里计算24拆成23*2的形式,由于之前23计算过,所以4次减少成了1次。
矩阵快速幂同理,不过我们要先从递推表达式中抽取出转移矩阵。
第一步:找到转移矩阵:

我们发现斐波那契数列可以提取的永恒的矩阵
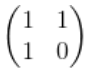
当我们不断往回推会发现最后变成

这个矩阵的n-1次方乘以一个f1和f2组成2行1列的矩阵
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=1000000007;
typedef vector<ll> vec;//不定一维数组
typedef vector<vec> mat;//不定二维数组
//矩阵乘法,输入矩阵a和矩阵b
mat mul(mat &a,mat &b)
{
mat c(a.size(),vec(b[0].size())); //矩阵相乘a*b 的矩阵与b*c的矩阵相乘得到a*c的矩阵
for(int i=0; i<2; i++)//行更新
{
for(int j=0; j<2; j++)//列更新
{
for(int k=0; k<2; k++)
{
c[i][j]+=a[i][k]*b[k][j];//一行乘以一列
c[i][j]%=mod;
}
}
}
return c;
}
mat pow(mat a,ll n) //快速幂
{
mat res(a.size(),vec(a.size()));
//把res作为单位矩阵乘以a矩阵的规模
for(int i=0; i<a.size(); i++)
res[i][i]=1;//单位矩阵;
while(n)
{
if(n&1) res=mul(res,a);
//让a矩阵乘以log2N次,
a=mul(a,a);
n/=2;
}
return res;
}
//a矩阵设为1101矩阵
ll solve(ll n)
{
mat a(2,vec(2));
a[0][0]=1;
a[0][1]=1;
a[1][0]=1;
a[1][1]=0;
a=pow(a,n);
return a[0][1];//也可以是a[1][0];
}
//主函数测试
int main()
{
ll n;
while(cin>>n&&n!=-1)
{
cout<<solve(n)<<endl;
}
return 0;
}
我们可以看出矩阵快速幂的求解,矩阵乘法是常数级,while时间复杂度为O(log2N)
我们再次将时间复杂度降低到了log级别,而且几乎没有用到什么空间。
第六种解法: 公式求解
斐波那契的通项公式用数学方式已经求解出来,我们可以直接用代码将公式打上:
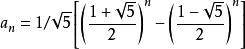
#include <csdio>
#include <iostream>
int main(){
int n;
std::cin>>n;
result = 1/5^0.5 * ((1 + 5^0.5)/2)^n - ((1 - 5^0.5)/2)^n);
std::cout<<result;
}
この方法は、ほとんどのバグで、** O(1)**解決は、数学は本当に規律のベストです。
