モンテカルロアルゴリズムは、私の意見では、はるかに少ないシミュレートされた実際のデータを取得するコストよりも、シーンとシミュレートされた大量のデータをシミュレートすることができ、実際のデータとほぼ同じであってもよいが、非常に不思議なアルゴリズムです。 。
今日、私は2つの単純なシミュレーションを行うために、モンテカルロアルゴリズムを使用します。π値は、さらに直交計算されます。
、π値
どのようにπの値が無理数ではなく、無限ループで、AD 480の周りに、数学者祖は、7小数点以下の結果の北部と南部の王朝に突入今日、私たちは私のシミュレーション結果をシミュレートするためにコンピュータを使用します。
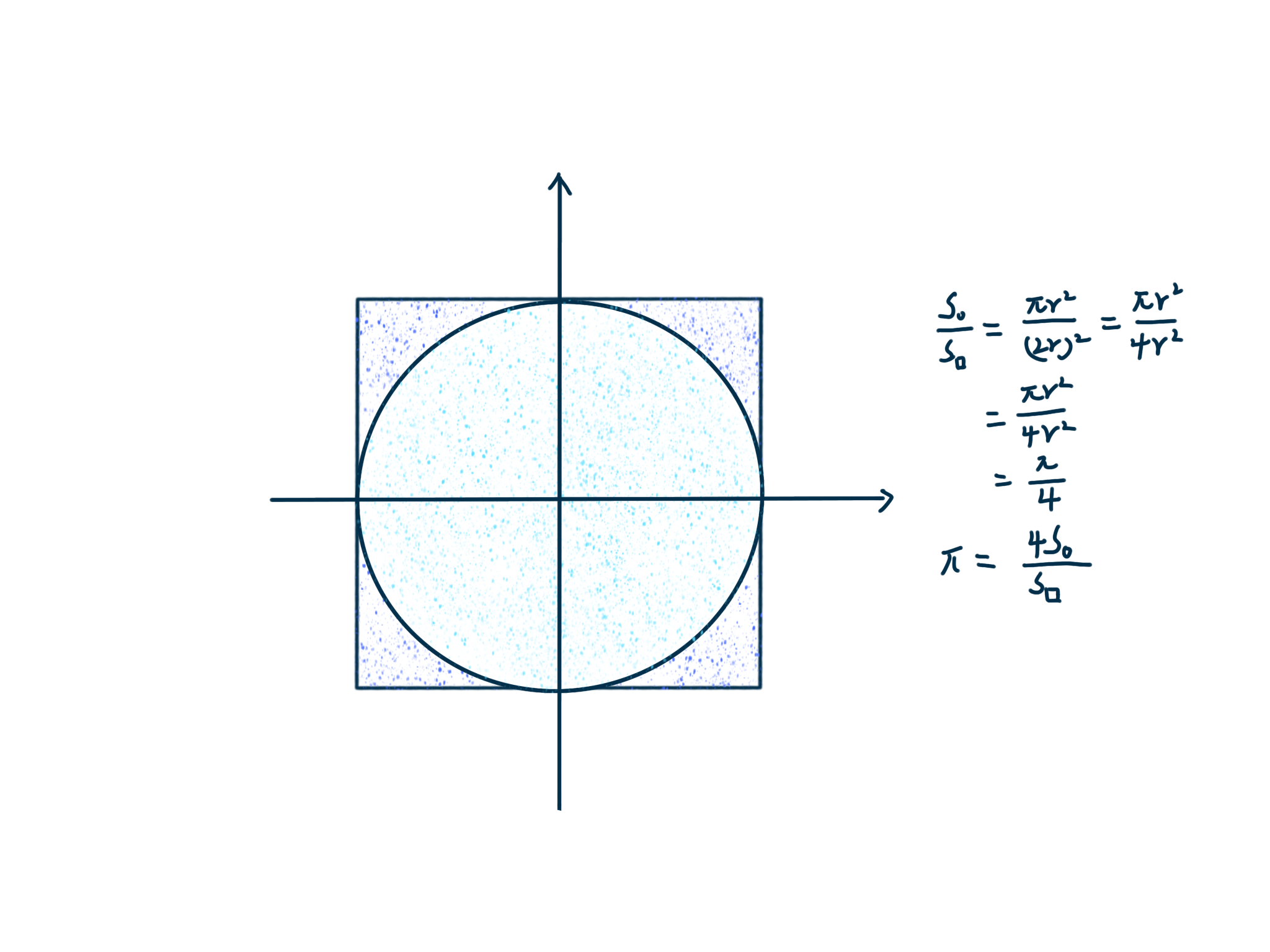
まず、シミュレーションの概念を説明するために、以下に示すように、限り、面積比がタリア算出されるように、我々はπを取得することができ、内接円の比例関係と正方形領域によって導出されます。
次に、どのように、πを使用せずに内接円の面積を計算します。内接円の内部領域内にXがある場合、我々は、ドット方式、n個のランダムなドットの正方形の領域を使用することができ、面積比がタリアであるN / X。この大規模なn個の場合、結果は非常に正確です。
次のように特定のコード
list_p=[]
list_p_x=[]
max_count = 100000000
first_count =10
rate = 2
count_s = 0
j=0
while first_count < max_count:
print(first_count)
while j < first_count:
x = random.uniform(-1, 1)
y = random.uniform(0, 1)
if x**2 + y**2 < 1:
count_s = count_s + 1
j = j + 1
list_p_x.append(first_count)
list_p.append(count_s/first_count*4)
j=0
count_s=0
first_count =first_count * rate
plt.xlim(0,first_count/2)
plt.ylim(3,3.3)
plt.plot(list_p_x,list_p)
plt.hlines(y=np.pi,xmin= first_count,xmax=list_p_x, colors = "c", linestyles = "dashed")
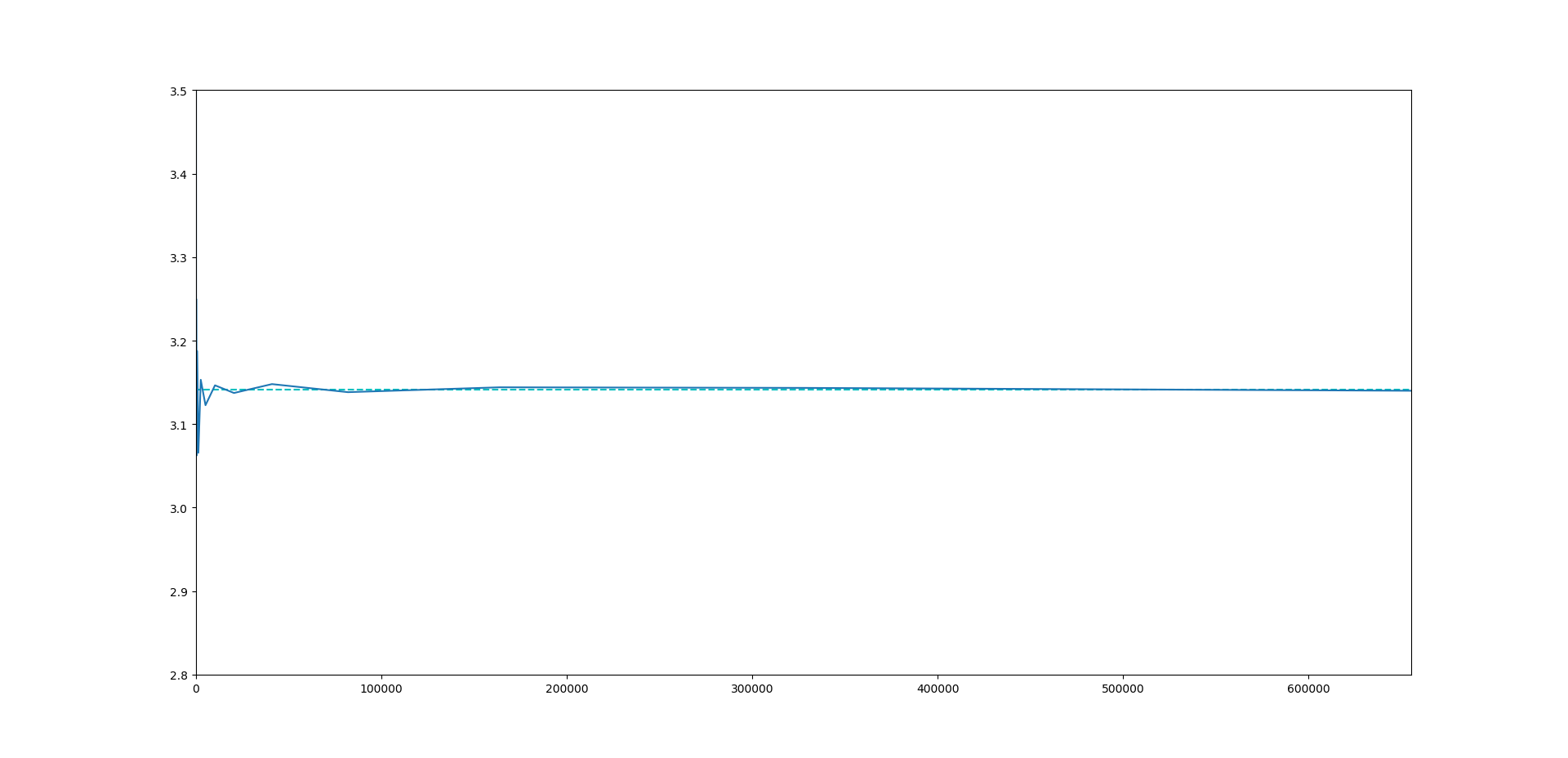
模拟出来的结果如下,在模拟超过1w次后,结果已经趋于稳定,基本等于3.14,这已经基本我们大部分使用场景。
二、积分
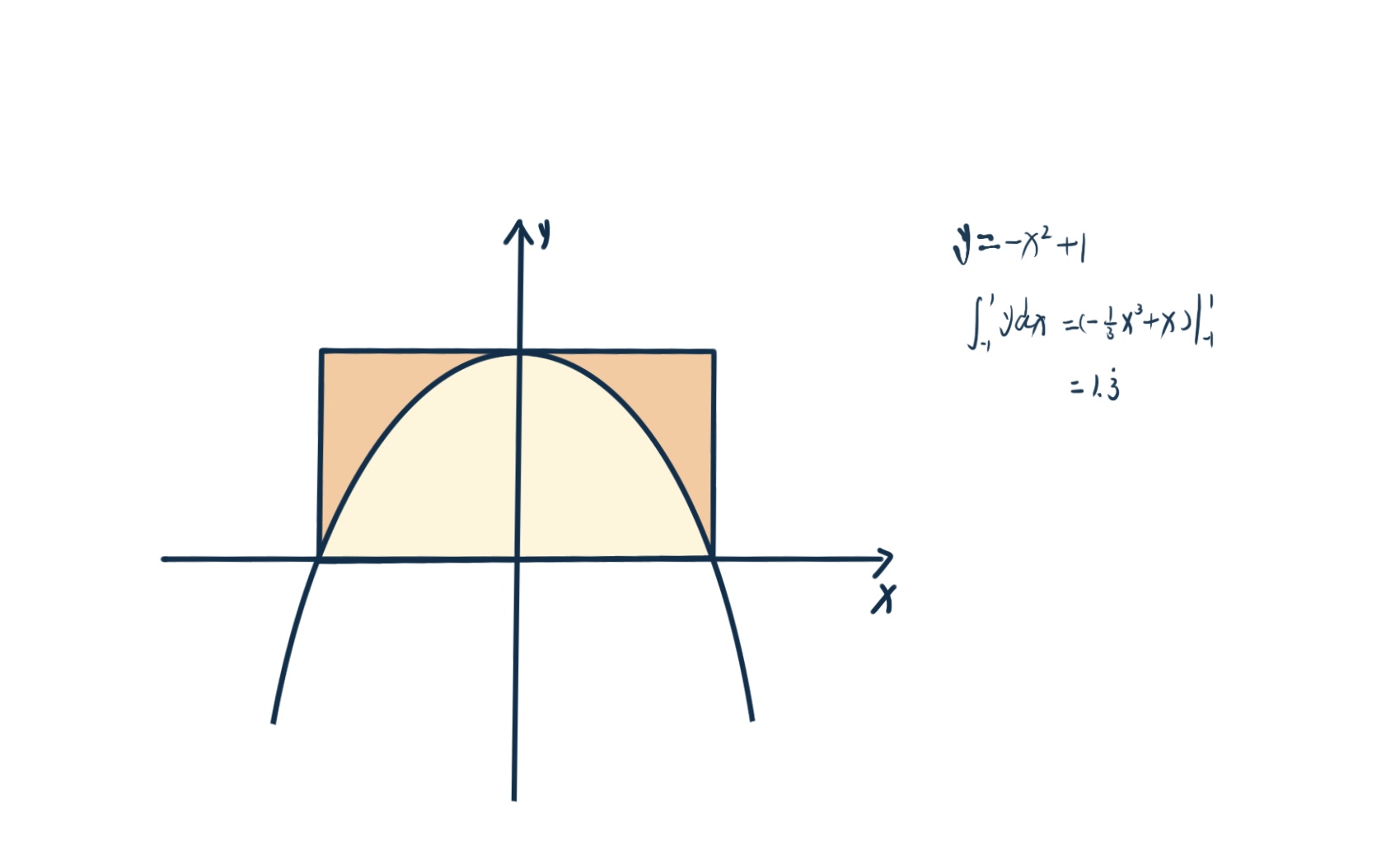
积分实际也可以理解是计算面试,比如下图,是y = -x^2+1 的函数图形,现在用蒙特卡罗求一下该函数的积分。
思路和求π得方法一致,也是通过随机打点的方式,根据在积分区域的散点数与矩形区域内散点数之比,乘以矩形面积,就是该积分区域面积。
分析模拟结果如下图,可以看到模拟3w到多次时,准确率很高了,与1.33不断接近,在9w次之后,基本保持重叠。

通过蒙特卡罗模拟,生成一系列符合预期要求的随机数,就可以模拟出一个十分接近实际值得近似值,十分适应于对数值计算精度要求不是很高的场景,比如,我们在计算圆面积的是,通常都会取3.14,而不会取3.1415926.....等。
注:
公众号:数据志(原:跟着菜鸟一起学R语言)
原文链接:https://www.cnblogs.com/wheng/articles/11832476.html