ベクトルの外積
定義
\ [\ BfのとVEC B \ \回= | \事と|| \ BFのB |罪\シータ\]
証明します
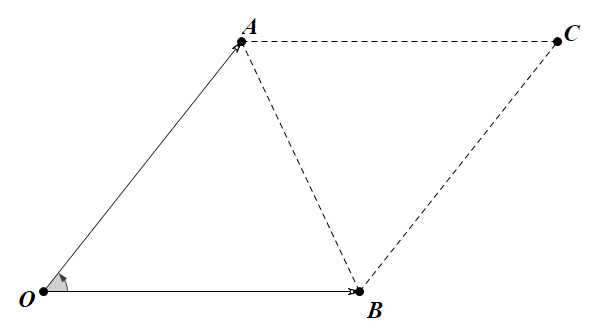
- 証明:並行四辺形0ACBに示すように\ [S _ {\デルタAOC } = \ FRAC {1} {2} | \ VEC {A} || \ VEC B |罪\シータ\]
- 平行四辺形の面積である\ [S = | \ VEC {A} | | \ VEC B |のSiN \シータ\]
\ [\ VEC A \ CDOT \ VEC B = | \ VEC A | | \ VEC B | COS \シータ\]
\ [COS \シータ= FRAC \ {\ VEC A \ CDOT \ VEC {B} | \ VEC | | \ B VEC |} \]
\ [\開始{eqnarray}罪\シータ&=&\のSQRT {1-COS ^ 2 \シータ} \\&=&\のFRAC {\のSQRT {(| \ VEC | ^ 2 \ CDOT | \ VEC B | )^ 2 - (\ VEC {A} \ CDOT {\ VEC {B})^ 2}}} {| \ VEC A || \ VEC B |} \\ \端{eqnarray} \]
\開始{eqnarray}
S&=&\ SQRT {(| \ VEC | ^ 2 \ CDOT | \ VEC B |)^ 2 - (\ VEC {A} \ CDOT {\ VEC {B})^ 2}} \
&=&\ SQRT {(X_1 ^ 2 + Y_1 ^ 2)(X_2 ^ 2 + Y_2 ^ 2) - (x_1x_2 + y_1y_2)^ 2} \
&=&\のSQRT {(x_1y_2)^ 2 +(x_2y_1) ^ 2-2x_1x_2y_1y_2} \
&=&\ SQRT {(x_1y_2-x_2y_1)^ 2} \
&=&| x_1y_2-x_2y_1 | \
\端{eqnarray}