SVD
動作の一種類の積を因数分解すると、マトリックス3内にマトリックスであります
その中でも、特異値行列は対角行列であります
Key_Function
np.linalg.svd関数行列の特異値分解であってもよいです。
U:直交行列
シグマ:特異値の対角行列の配列、他の非対角要素が0であります
V:直交行列
np.diag機能は、特異値の完全な行列を描きます
コード
インポートnumpyのNP AS A = np.mat(" 4 14 11; -2 8. 7 " ) 印刷(A) '' ' [14 4 11] 。[-2 8 7]] ' '' U-、シグマ、V = np.linalg.svd(A、full_matrices = 偽) プリント(U-) '' ' [[-0.9486833 -0.31622777] [-0.31622777 0.9486833]] ' '' プリント(Sigma)を #シグマ特異値の対角行列のみ値 '' ' [18.97366596 9.48683298] ' '' プリント(np.diag(シグマ)) '' ' [0の18.97366596ザ] [0の。9。48683298]] ''」 印刷(V) '' ' [[-0.33333333 -0.66666667 -0.66666667] [0.66666667 0.33333333 -0.66666667]] ' '' プリント(U * np.diag(Sigma社製)* V) '' ' [[4 11 14] [8. 7 -2]] '' '
一般逆行列
Key_Function
np.linalg.pinv機能
np.inv機能
コード
インポートnumpyのNP AS A = np.mat(" 4 14 11; -2 8. 7 " ) 印刷(A) '' ' [14 4 11] [-2 8. 7]] ' '' pseudoinv = np.linalg。 PINV(A) プリント(pseudoinv) '' ' [[-0.00555556 0.07222222] [0.02222222 0.04444444] [0.05555556 -0.05555556]] ' '' プリント(*のpseudoinv) '' ' 単位行列に非常に近い [1.00000000e + 00 0.00000000 00 + E] [8.32667268e-1.00000000e。17 + 00]] '' '
数学的概念

一般逆行列の定義

若しくは
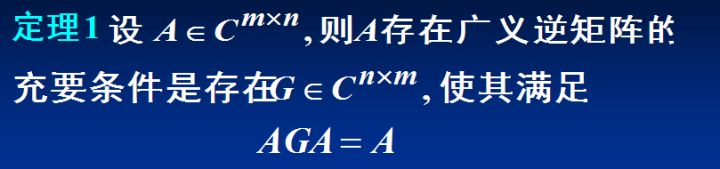
一般逆行列を解きます

行列式
Key_Function
Np.linalg.det決定因子関数演算行列
コード
インポートのNPとしてnumpyの A = np.mat(" 3 4 5 6 " ) 、印刷(A) '' ' [[3 4] [5,6] ''' の印刷を(np.linalg.det(A)) #-2.0