所与\(H * W \)のみボード上のボード、\(N \)正方形が黒色であり、他方が白グリッドです。
ボードの左上隅には兵士、グリッド右またはダウンすることができますすべてのステップがあり、そして黒のグリッドに移動することはできません。右下のストロークに左上からの要求、可能なルートの数は、総
\(1 \ルH W \ル10 ^ 5,1 \ルN \ル2000 \) 出力\(10 ^ 7 + 9 \)モジュロ
H、巨大なW、DPの一般的には、どのように黒のグリッド数を検討する必要はありません
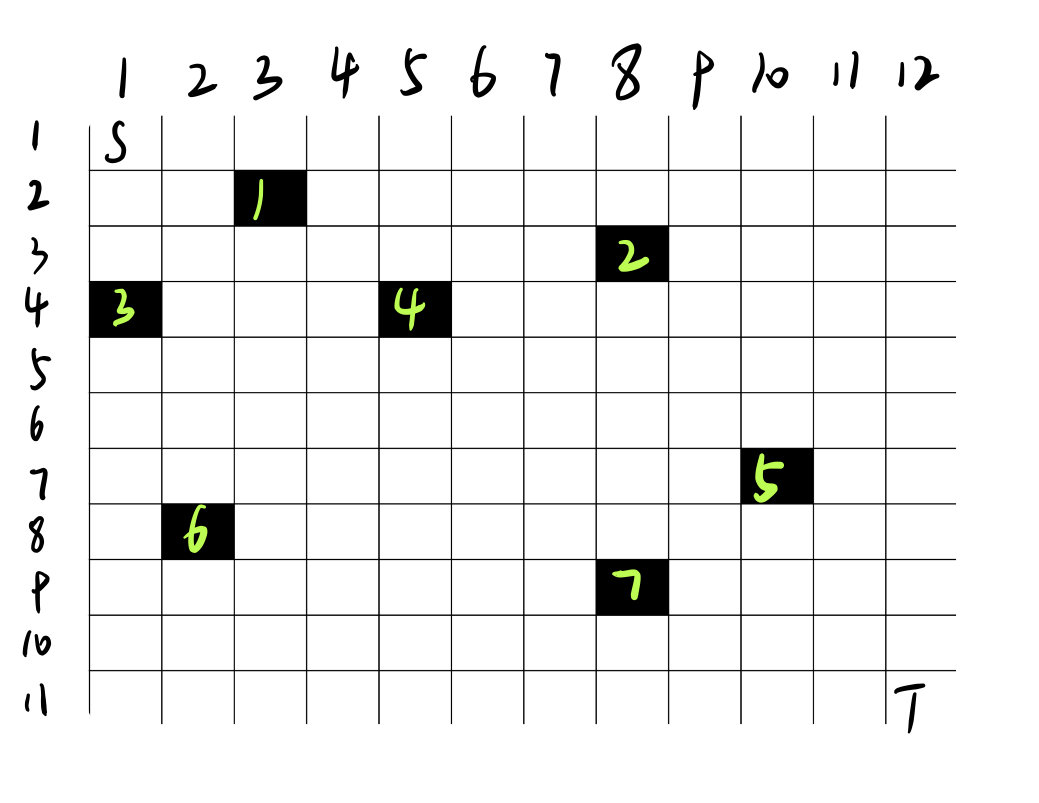
Sから片の総数であり、数学的知識の組み合わせからTパスに見\(2-Wは、Hであり、C_ {H +が} 1} ^ {\) 、ブラック格子の少なくともストリップを介してパス数を減算することにより答えであります。
それでは、どのようにそれを数え漏れないのですか?
パスの総数が持っている、Sから第4号に、例えば、グリッドブラック4(4,5)に黒のグリッドを含む最初の経路を介して、少なくともブラックグリッドのそれぞれを検討C_ {4 + 5(\ 4-1 -1-1} ^ {} \)セクション、長い三つの除外後及び4のストリップを通るパスの数、黒格子なしでは、Sからのパスの数です。どのように排除するには?実際に、我々は、以前に限り、それぞれ3倍として、黒格子縞複数のパスことなく1に、ときに別々に3 Sを算出した黒格子縞複数のパス4せず、SをオペレータSを計数しました4に、1〜4の番号へのすべてのパス。
行及び列に応じてすべての黒グリッドが設けられ、ソート順を昇順座標\(F [i]が\) Sから最初に\(Iは\)格子、パスの数を介して他の鉄トレリス通過しない方法
[\をF [I] = C_ {X_I-1 + y_i- 1} ^ {X_I-1} - \ sum_ {J = 1} ^ {I-1} F [j] * C_ {X_I-X - jが+ Y_I-y_j} ^ {X_I-X - jが}、X_IはY_I \ GEは、GEのX - jがを\ここで X - jが\]
非分裂「積分」の構成の基準点の周りに、一般に「基準点」を探して、カウント動的計画法を解くときに、サブ間の問題を回避するためオーバーラップ
#include <bits/stdc++.h>
using namespace std;
const int mod = 1e9+7;
const int N = 2e5+10;
typedef long long ll;
typedef pair<int,int> pii;
#define fi first
#define se second
ll jc[N],inv[N];
int h,w,n;
ll f[2010];
pii a[2010];
ll ksm(ll a,ll b){
ll res = 1;
for(;b;b>>=1){
if(b & 1)res = res * a % mod;
a = a * a % mod;
}
return res;
}
int C(int x,int y){
return jc[x] * inv[y] %mod * inv[x-y] % mod;
}
int main(){
jc[0] = 1;inv[0] = 1;
for(int i=1;i<N;i++)jc[i] = jc[i-1] * i % mod,inv[i] = ksm(jc[i],mod-2);
scanf("%d%d%d",&h,&w,&n);
for(int i=1;i<=n;i++)scanf("%d%d",&a[i].fi,&a[i].se);
sort(a+1,a+1+n);
a[n+1].fi = h;a[n+1].se = w;
for(int i=1;i<=n+1;i++){
int x = a[i].fi,y = a[i].se;
f[i] = C(x+y-2,x-1);
for(int j=1;j<i;j++){
int xj = a[j].fi;
int yj = a[j].se;
if(xj > x || yj > y)continue;
f[i] = (f[i] - (ll)f[j] * C(x-xj+y-yj,x-xj)%mod + mod)%mod;
}
}
printf("%lld\n",f[n+1]%mod);
return 0;
}