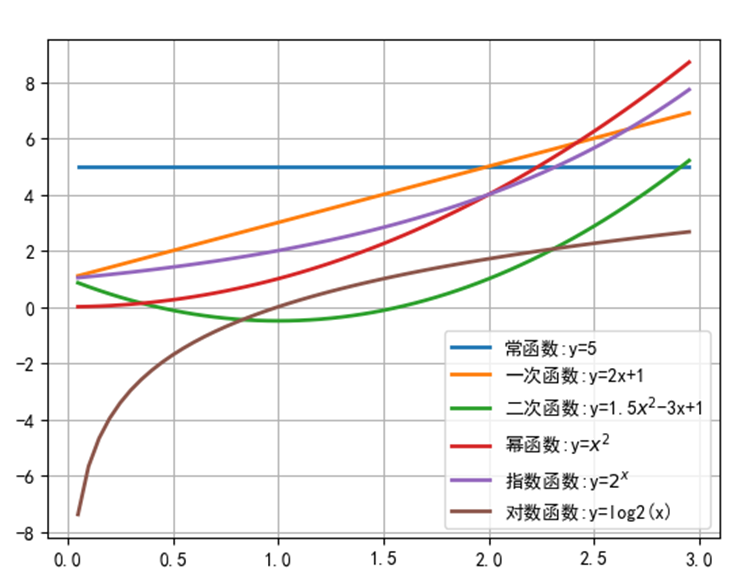
共通機能
定数関数: ![]()
一つの機能:![]()
二次関数:![]()
電源機能:![]()
指数関数:![]() 、Aは、範囲内である:A> 0&≠1
、Aは、範囲内である:A> 0&≠1
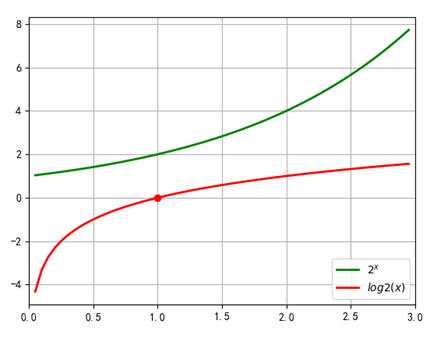
対数関数:![]() 、Aは、範囲内である:A> 0&≠1
、Aは、範囲内である:A> 0&≠1

数の計算
![]()
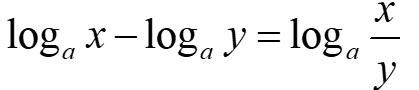
インデックスの操作

派生物
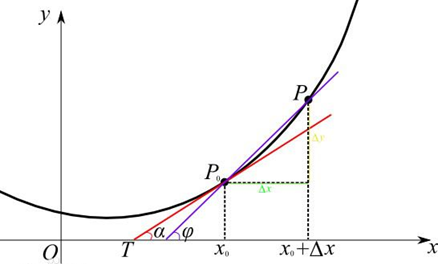
この点の付近に記載関数の導関数の変化の速度の関数が曲線における点の関数と考えることができるいくつかの点で、この点における接線の傾きによって表される関数の誘導体です。その点での関数の変化微分の値が大きいほど、大きくなります。
定義:X = X0における関数Y = F(x)が変数増分Δxだけから生成される場合、Δyがデルタ、Δの存在下でのxと、△Xの出力値の増加との間の比の関数とは、0ときに近づい限界値Aが、それはX0における導関数の値の関数です。
![]()
一般的な導関数
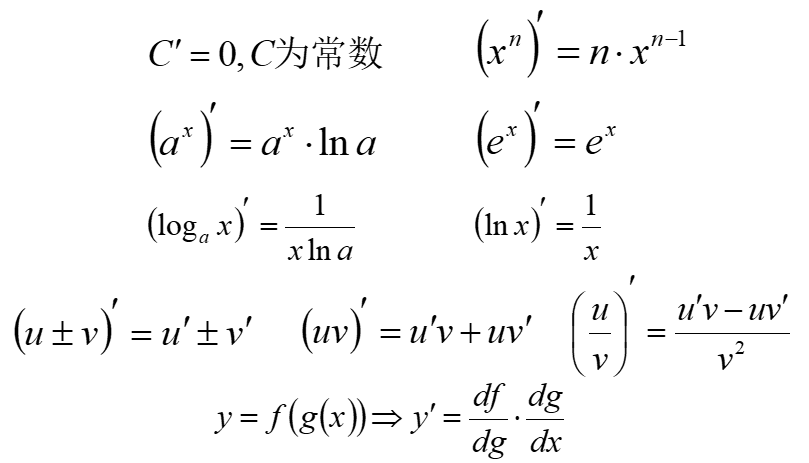
偏微分
一定の他の変数を維持しながら、多変数関数では、部分的誘導体に誘導体は可変です。想定バイナリ関数z = f(x、y)は、点(X0、YO)が定義内のポイントは、増分のY-Y0、X0とXに固定されている、△X、対応する増分関数z ΔZ= F(X 0 +ΔX、Y0) - F(X0、Y0)、ΔZ、△X及び比率は0に近づくときに存在する場合、△xは、限界値であり、次いで、リミット機能は、Z = F(Xと呼ばれています、y)は()偏導関数のXの部分的誘導体であります

(2,1)におけるxの偏微分でZ = X2 + XY2 =
勾配
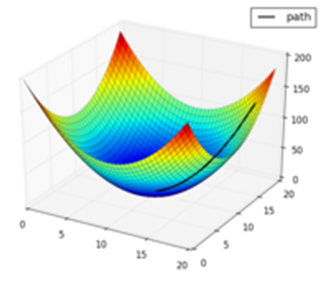
勾配:勾配は、その方向にその時点で撮影した方向における導関数の最大値は、この時点での変化の最速の機能に沿って、すなわち方向、変化の最大速度(すなわち、勾配ベクトルを表すベクトルであります金型)

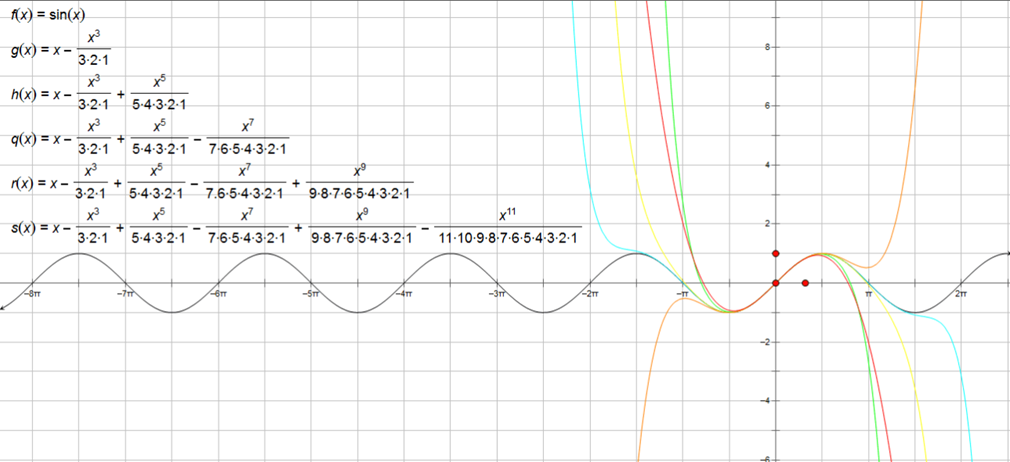
テイラー式
テイラー(テイラー)式は近傍の地点に関する情報が式の関数値によって記述されます。関数は、それぞれの第1の微分値の点の場合に知られている機能で十分に平滑である場合は、テイラー式伝導係数値はこの点近傍の多項式近似関数を構築するためにこれらの値を使用することができます。
若函数f(x)在包含x0的某个闭区间[a,b]上具有n阶函数,且在开区间(a,b)上具有n+1阶函数,则对闭区间[a,b]上任意一点x,有Taylor公式如下:<f(n)(x)表示f(x)的n阶导数,Rn(x)是Taylor公式的余项,是(x-x0)n的高阶无穷小
简言之:利用x0点的导数信息来近似逼近该点邻域的原函数。
![]()
![]()
Taylor公式的应用
![]()
古典概率
概率是以假设为基础的,即假定随机现象所发生的事件是有限的、互不相容的, 而且每个基本事件发生的可能性相等。一般来讲,如果在全部可能出现的基本事 件范围内构成事件A的基本事件有a个,不构成事件A的有b个,那么事件A出现的 概率为:
![]()
概率体现的是随机事件A发生可能的大小度量(数值)
联合概率
表示两个事件共同发生的概率,事件A和事件B的共同概率记作:P(AB)、P(A,B) 或者P(A∩B),读作“事件A和事件B同时发生的概率”
条件概率
事件A在另外一个事件B已经发生的条件下的 发生概率叫做条件概率,表示为P(A|B),读作 “在B条件下A发生的概率“ ,一般情况下 P(A|B)≠P(A),而且条件概率具有三个特性:
非负性,可列性,可加性
![]()
将条件概率公式由两个事件推广到任意有穷多个事件时,可以得到如下公式,假 设A1,A2,....,An为n个任意事件(n≥2),而且P(A1A2 ...An )>0,则:
![]()
全概率公式
样本空间Ω有一组事件A1、A2 ...An , 如果事件组满 足下列两个条件,那么事件组称为样本空间的一个 划分:
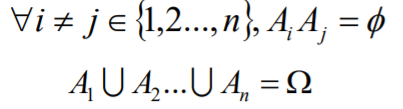
设事件{Aj}是样本空间Ω的一个划分,且P(Ai)>0, 那么对于任意事件B,全概率公式为:
![]()
贝叶斯公式
设A1、A2 ...An是样本空间Ω的一个划分,如果 对任意事件B而言,有P(B)>0,那么:
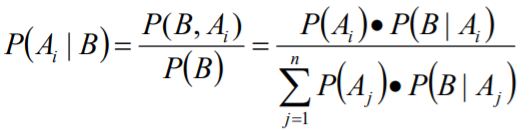
贝叶斯的推导
![]()
![]()
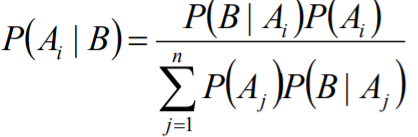
期望
期望(mean):也就是均值,是概率加权下的“平均值” ,是每次可能结果的概率乘 以其结果的总和,反映的实随机变量平均取值大小。常用符号μ表示 :
连续性数据:![]()
离散性数据: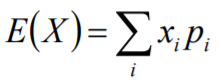
![]()

假设C为一个常数,X和Y实两个随机变量,那么期望有一下性质:
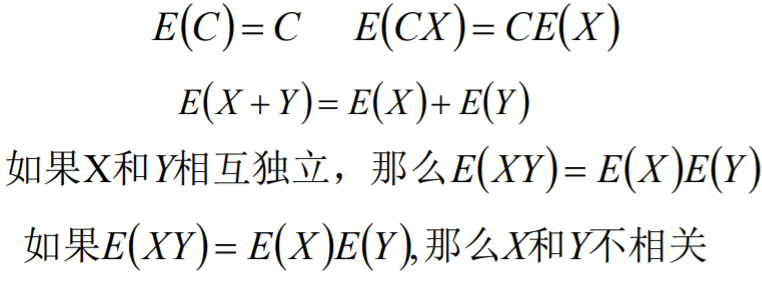
方差
方差(variance)是衡量随机变量或一组数据时离散程度的度量,是用来度量随机 变量和其数学期望之间的偏离程度。即方差是衡量数据原数据和期望/均值相差的 度量值。
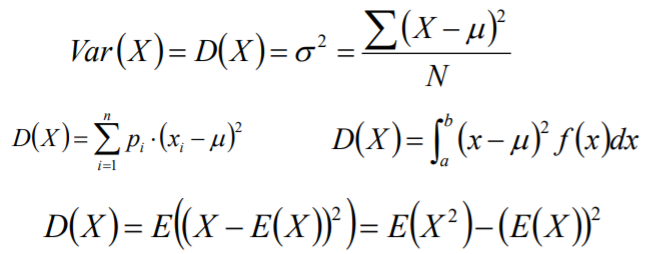

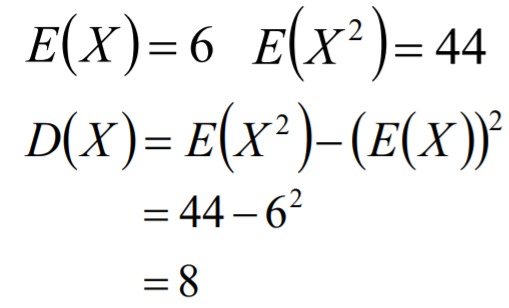
假设C为一个常数,X和Y实两个随机变量,那么方差有一下性质
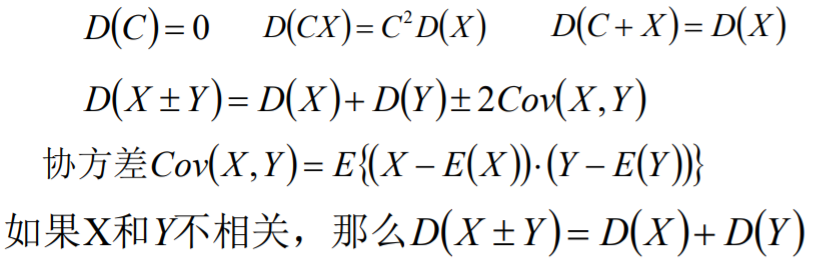
标准差
标准差(Standard Deviation)是离均值平方的算术平均数的平方根,用符号σ表示, 其实标准差就是方差的算术平方根。
标准差和方差都是测量离散趋势的最重要、最常见的指标。标准差和方差的不同 点在于,标准差和变量的计算单位是相同的,比方差清楚,因此在很多分析的时 候使用的是标准差。
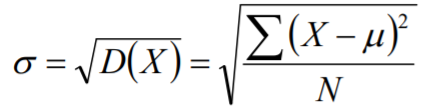

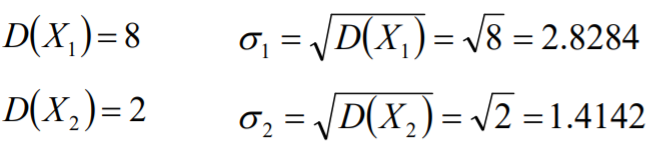
协方差
协方差常用于衡量两个变量的总体误差;当两个变量相同的情况下,协方差其实 就是方差。
如果X和Y是统计独立的,那么二者之间的协方差为零。但是如果协方差为零, 那么X和Y是不相关的。

假设C为一个常数,X和Y实两个随机变量,那么协方差有性质如下所示:
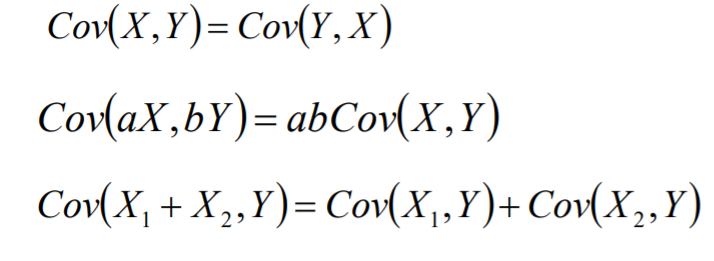
协方差是两个随机变量具有相同方向变化趋势的度量:
若Cov(X,Y) > 0, 则X和Y的变化趋势相同;
若Cov(X,Y) < 0, 则X和Y的变化趋势相反;
若Cov(X,Y) = 0,则X和Y不相关,也就是变化没有什么相关性

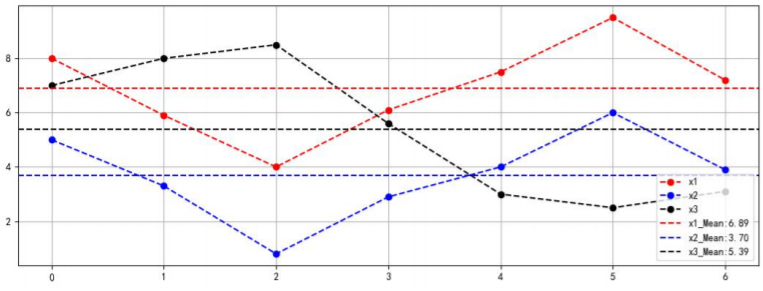
协方差矩阵
对于n个随机向量(X1 ,X2 ,X3 ....Xn ), 任意两个元素Xi和Xj都可以得到一个协方差, 从而形成一个n*n的矩阵,该矩阵就叫做协方差矩阵,协方差矩阵为对称矩阵。
![]()
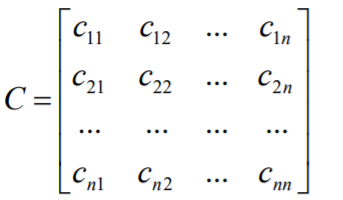
大数定理
大数定律的意义:随着样本容量n的增加,样本平均数将接近于总体平均数(期望 μ),所以在统计推断中,一般都会使用样本平均数估计总体平均数的值。
也就是我们会使用一部分样本的平均值来代替整体样本的期望/均值,出现偏差 的可能是存在的,但是当n足够大的时候,偏差的可能性是非常小的,当n无限大 的时候,这种可能性的概率基本为0。
大数定律的主要作用就是为使用频率来估计概率提供了理论支持;为使用部分数 据来近似的模拟构建全部数据的特征提供了理论支持。
中心极限定理
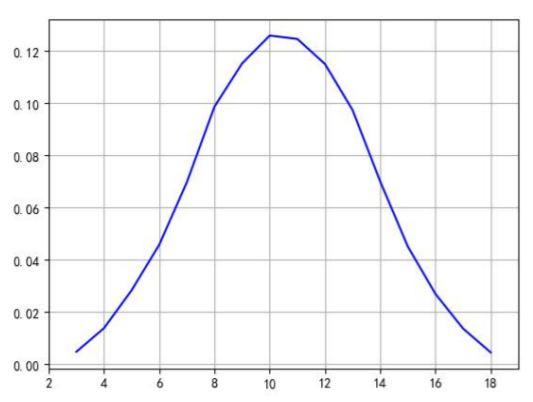
中心极限定理就是一般在同分布的情况下,抽样样本值的规范和在总体数量趋于 无穷时的极限分布近似于正态分布
随机的抛六面的骰子, 计算三次的点数的和, 三 次点数的和其实就是一 个事件A,现在问事件A 发生的概率以及事件A 所属的分布是什么?
最大似然估计
最大似然法(Maximum Likelihood Estimation, MLE)也称为最大概似估计、 极大似然估计,是一种具有理论性的参数估计方法。基本思想是:当从模型总体 随机抽取n组样本观测值后,最合理的参数估计量应该使得从模型中抽取该n组样 本观测值的概率最大;一般步骤如下:
1. 写出似然函数;
2. 对似然函数取对数,并整理;
3. 求导数;
4. 解似然方程
设总体分布为f(x,θ), {Xn}为该总体采样得到的样本。因为随机序列{Xn}独立同分 布,则它们的联合密度函数为:
![]()
这里θ被看做固定但是未知的参数,反过来,因为样本已经存在,可以看做{Xn} 是固定的,L(x,θ)是关于θ的函数,即似然函数; 求参数θ的值,使得似然函数取最大值,这种方法叫做最大似然估计法。
若给定一组样本{Xn},已知随机样本符合高斯分布N(μ,σ^2),试估计σ和μ的值
分布的概率函数:![]()
最大似然函数的乘积:![]()
对数似然:![]()
化简 :
![]()
![]()
![]()
要求似然函数l(x)最大,即l(x)求极值即可,将似然函数对参数μ和σ分别求偏导数:
![]()
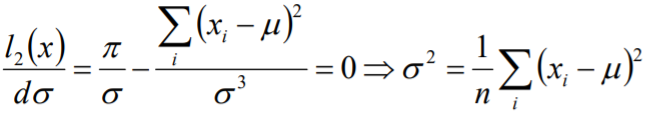
向量的计算
设两向量为:![]()
向量的加法/减法满足平行四边形法则和三角形法则

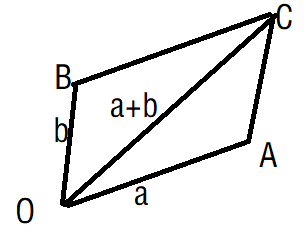
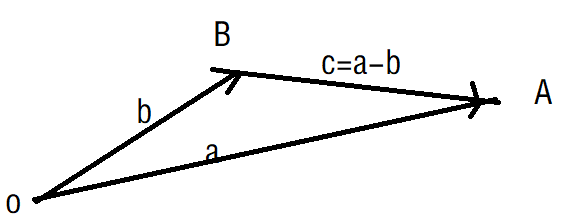
数乘:实数λ和向量a的叉乘乘积还是一个向量,记作λa,且|λa|=λ|a|;数 乘的几何意义是将向量a进行伸长或者压缩操作
![]()
向量的运算
设两向量为:![]() 并且a和b之间的夹角为:θ
并且a和b之间的夹角为:θ
数量积:两个向量的数量积(内积、点积)是一个数量/实数,记作 ![]()
![]()
向量积:两个向量的向量积(外积、叉积)是一个向量,记作![]() ; 向量积即两个不共线非零向量所在平面的一组法向量。
; 向量积即两个不共线非零向量所在平面的一组法向量。
![]()
矩阵的直观表示
数域F中m*n个数排成m行n列,并括以圆括弧(或方括弧)的数表示 成为数域F上的矩阵,通常用大写字母记作A或者Am*n,有时也记作 A=(aij)m*n(i=1,2…,m;j=1,2,…n),其中aij表示矩阵A的第i行的第j列 元素,当F为实数域R时,A叫做实矩阵,当F为复数域C时,A叫做 复矩阵。
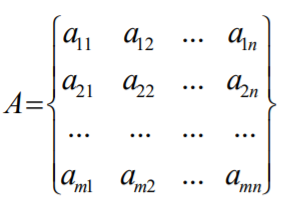
矩阵的加减法
矩阵的加法与减法要求进行操作的两个矩阵A和B具有相同的阶, 假设A为m*n阶矩阵,B为m*n阶矩阵,那么C=A B也是m*n阶的 矩阵,并且矩阵C的元素满足:
![]()

![]()
![]()
![]()
矩阵与数的乘法
数乘:将数λ与矩阵A相乘,就是将数λ与矩阵A中的每一个元素相 乘,记作λA;结果C=λA,并且C中的元素满足![]()
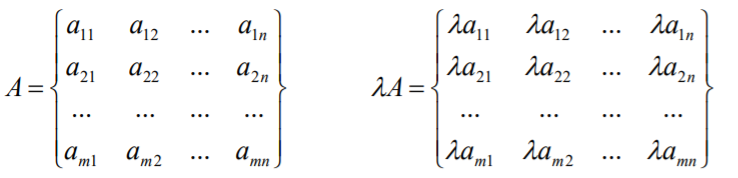
数乘:![]()

假设A为m*n阶矩阵,x为n*1的列向量,则Ax为m*1的列向量,记 作![]()
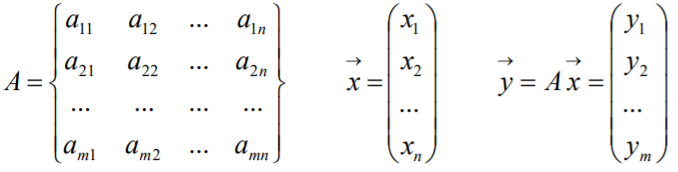

矩阵的乘法
仅当第一个矩阵A的列数和第二个矩阵B的行数相等时 才能够定义,假设A为m*s阶矩阵,B为s*n阶矩阵,那么C=A*B是 m*n阶矩阵,并且矩阵C中的元素满足![]()

乘法的前提 :左列==右行
由于这个python库里面有广播机制,所以用一个m*n的矩阵可以和n个元素列矩阵做乘积:
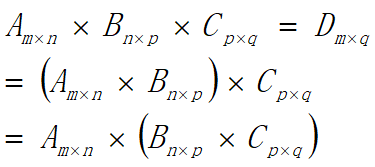
![]()
![]()
![]()
In [1]: import numpy as np In [2]: a = np.array([[1,2],[2,3],[4,5]]) In [3]: a Out[3]: array([[1, 2], [2, 3], [4, 5]]) In [4]: b = np.array([[1,2],[2,2]]) In [5]: a.dot(b) Out[5]: array([[ 5, 6], [ 8, 10], [14, 18]])
广播机制
from numpy import * import numpy as np # 创建随机矩阵: np.random.rand(2,2) #注意没有多余的() # 创建随机矩阵: np.random.random((2,2)) #注意有多余的() # 创建3*3的0-10之间的随机整数矩阵: np.random.randint(10,size=(3,3)) # 创建2-8之间的随机整数矩阵: np.random.randint(2,8,size=[2,5]) # 创建正态分布矩阵: np.random.normal(mean,stdev,size), 如,np.random.normal(1,0.1,(3,4)) 给出均值为mean,标准差为stdev的高斯随机数,size矩阵shape # 创建标准正态分布矩阵: np.random.randn(d0, d1, ..., dn) ,如np.random.randn(3,4)
逆矩阵
逆矩阵:如果 A 是一个m x m 矩阵, 并且如果它有逆矩阵。
矩阵与其逆阵的乘积等于单位阵:![]()
不是所有的矩阵都有逆矩阵
没有逆矩阵的矩阵称为“奇异矩阵” 或“退化矩阵”。
转置矩阵
行变列,列变行
![]()

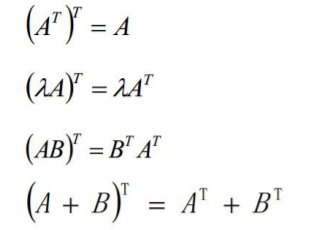
特征值分解(QR分解)
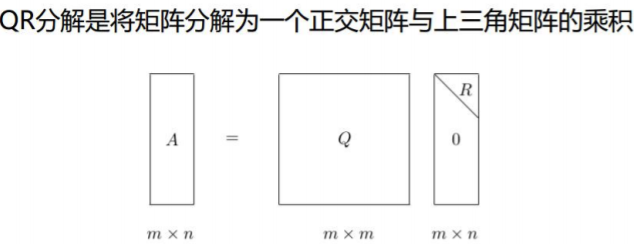

SVD分解
奇异值分解(Singular Value Decomposition)是一种重要的矩阵分 解方法,可以看做是对称方阵在任意矩阵上的推广
假设A为一个m*n阶实矩阵,则存在一个分解使得:
![]()
通常将奇异值由大到小排列,这样Σ便能由A唯一确定了。
向量的导数(极其重要)
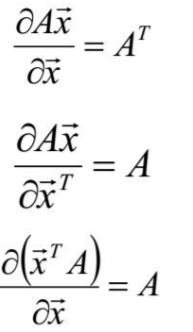
标量对向量的导数


A为n*n的矩阵,|A|为A的行列式,计算![]()