先行レビュー:
アダマール変換、パリティ問題:(a)の量子単純なアルゴリズム
さて、本物の物語、サイモンのアルゴリズム
問題:
秘密文字列、nビット0の文字列\(S \ {0,1における\ \} ^ N \)
今ブラックボックスで、f彼は約(x)は、我々が唯一知っている(F(X-)= F(X-の\ oplusのS)\)\、X-入力は、nは0,1文字列のビットである\は、(X \ \ {0,1 \} ^ Nで \)
私たちは秘密の文字列を見つけることができますどのように多くの時間、頼みますか?
クラシックソリューション:
我々は見つけることができた場合は(X \)\と\(X- \のoplus S \)それは非常に簡単です、あなたは限り、Sを得ることができます\(X- \のoplus S \ oplus X- \) 。
だから、両方の入力が同じ出力にそれを見つける必要がある場合は?
実際には、これは我々が変形の問題に精通しているもう一つの問題は、人々は2人の誕生日が同じである必要がありどのように多くの人々のグループ、23人は2人が、50%以上の同じ誕生日の確率であることを印象です60人がいる場合は、同じ誕生日の確率の2人が99%以上という。
問題と解決策の誕生日の問題は後に関係なく、どのように疲れて同じではない、とあなたは私たちが一般的な答えがされ与える誕生日の問題の検索、知りたい\を(2 ^ {N / 2 } \) c倍。
量子ソリューション:
3段階の合計量子ソリューション:
- 設定ランダム重ね合わせの$ \のFRAC {1} {\ SQRT2} | R \ rangle + \ FRAC {1} {\ SQRT2} | R \ oplus S \ rangle $
- ランダムYを得るためにフーリエサンプル:\(Y・S)2 = 0(\ MOD \)
- 反復ステップのn-1倍のn-1の線形方程式を生成します。
次に、各ステップで何をすべきかを段階的に見て、それを行う方法:
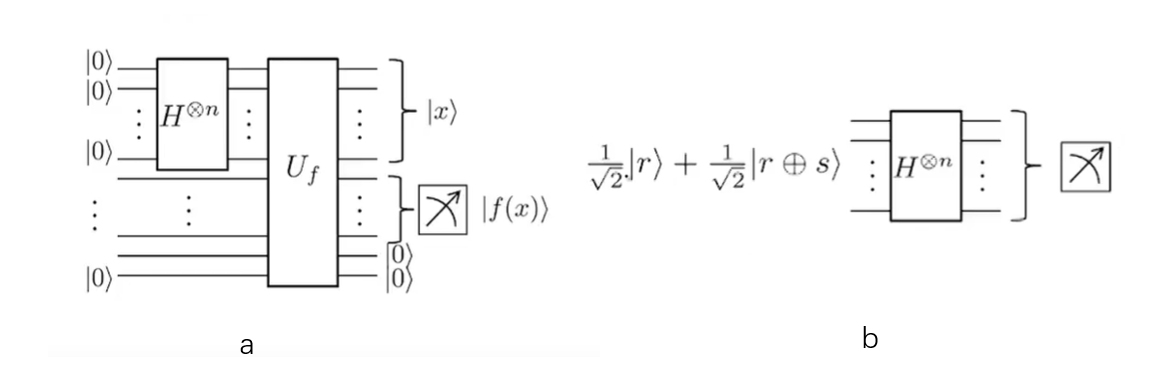
最初のステップ重ね合わせ$ \のFRACの製造は、{1} {\ SQRT2} | R \ rangle + \ FRAC {1} {\ SQRT2} | R \ oplus S \ rangle $、 。これは、図A.することによって達成することができます
まず最初の\(H ^ {\は、nをotimes } \) ドア、我々のnビット\(| 0 \ rangleが\)正常重ね合わせ状態の$ \のFRACなる{1} {2 ^ {\ FRAC {n}が{2}}} \ SUM_X | X \ rangle $
そして\(| B \ rangle \)と共にを通して\(U_f \) 、結果は$ \ FRAC {1} {2 ^ {\ FRAC {n}は{2}}} \ SUM_X | X \ rangle | B \ oplusのf(x)が\ rangle $
測定|(\ rangle \ Bの\のoplusのF(X-))が\を、測定結果の結果のみである(| X \ rangle \)\さらに他\(| X \ rangle \)は、このブラックボックスに基づいて、崩壊しますR \ rangle $と|だけ$特性は、次に\ |(R \ oplus S \ rangle \) 、それらをfされているので(x)が同じである、とどまる、Rは任意の順序で、測定の結果は、どのに対応しますこれは、R rのです。
R \ rangle + \ FRAC {1} {\ SQRT2} | | R \ oplus S \ rangle $この時点では、重ね合わせ状態の$ \のFRAC {1} {\ SQRT2}を取得したいです
第二ステップ、フーリエサンプリング
R \ rangle + \ FRAC {1} {\ SQRT2} | | R \ oplus S \ rangle $フーリエサンプリング我々は$ \ FRAC {1} {\ SQRT2}の重ね合わせを得ます
再びにより\(H ^ {\は、nをotimes } \) 私たちは何を得ることができますか?
私たちによると、(a)は、単純な量子アルゴリズムの結論では、我々はそれを知っている\(H ^ {\は、nをotimes } | {U \ rangle = \ SUM_X \ FRAC {-1 ^ {U・X}}を2 ^ {\ FRAC N-2}}、{{}} | X \ rangle \)。
それから
\ [\開始H ^ {\ nはotimes} {整列}(\ FRAC {1} {\ SQRT2} | R \ rangle + \ FRAC {1} {\ SQRT2} | Rの\のoplus Sの\ rangleを)&= \ FRAC {1} {\ SQRT2} \ SUM_X \ FRAC {-1 ^ {R・X}} {2 ^ {N / 2}} | X \ rangle + \ FRAC {1} {\ SQRT2} \ SUM_X \ FRAC {-1 ^ {(R \ oplus S)・X}} {2 ^ {N / 2}} | X \ rangle \\&= \ SUM_X(\ FRAC {-1 ^ {R・X}} {2 ^ {(nは+1)/ 2}} + \ FRAC {-1 ^ {(R \ oplus S)・X}} {2 ^ {(N + 1)/ 2}})| X \ rangle \\&= \ SUM_X \ FRAC {1 ^ {R・X} +( - 1)^ {(R \ oplus S)・X}} {2 ^ {(N + 1)/ 2}} | X \ rangle \端{整列} \]
この時点で、我々は質問に焦点を当ててきた\(^ 1 {R・X - 1)^ {(R \ oplus秒)・X} \} +() で。
\(( - 1)^ { (R \ oplus S)・X} \) のように書くことができる\(( - 1)^ {S・X} *( - 1)^ {R&LT・X} \) (理由としてでき、あなたはすべてのビット演算、可能な4のも合計を試すことができます
各可能な方程式の確率は次のように書くことができる\(\ FRAC {(( - 1)^ {S・X} +1)*( - 1)^ {R・X}} {2 ^ {(N + 1 / 2)}} \)
もし\(S・X = 0 \ ) 、この確率を正確に\(\ FRAC {( - 1 )^ {R・Z}} {2 ^ {(N-1)/ 2}} \)
もし\(S・X = -1 \ ) だから、この確率は正確に0であります
だから、これは何を示していますか?
これは、我々が測定した場合ことを実証している(| X \ rangle \)\を、我々はX取得する必要があります\(S・X = 0 \ ) 、そして、彼らはゼロでオフセットする必要はありませんので。
そこで、Xを取得し、それが何を意味するのでしょうか?
\(S・X = 0 \ ) 私たちが得た実際には、方程式の$ s_1x_1 + s_2x_2 + ... + s_nx_n = 0 MOD 2 $ \
第三段階:
私たちが最初に測定した場合のx数\(X ^ 1 \) 、そして私たちを取得方程式の$ s_1x_1 ^ 1 + s_2x_2 ^ 1 + ...... + s_nx_n ^ 1 = 0 \ MOD 2 $
第二の測定、MOD 2 $ \ $ s_1x_1 ^ 1 + s_2x_2 ^ 1 + ... + s_nx_n ^ = 0~1の方程式
したがって、時刻n-1、N-1を測定する方程式の組の方程式を得ることができます。
$ s_1x_1 ^ 1 + s_2x_2 ^ 1 + ...... + s_nx_n ^ 1 = 0 \ MOD 2 $
$ s_1x_1 ^ 1 + s_2x_2 ^ 1 + ...... + s_nx_n ^ 1 = 0 \ MOD 2 $
......
$ s_1x_1 ^ {N-1} + s_2x_2 ^ {N-1} + ...... + s_nx_n ^ {N-1} = 0 \ MOD 2 $
N-1個の方程式、nは未知数(\(S_1、S_2、......、S_N \) )、一般に、溶液の二組が存在するであろう、自明な解集合は、全てゼロであり、これは米国ではなく、ソリューションの別のセットは、私たちの回答です\(S \) 。
成功の確率:
上記の式のソリューションこれは線形でない場合、これは、線形方程式系であるという前提があるには、対策のn-1回の答えを得ることは不可能です。
そして、Iからなる方程式xは線形方程式の確率はどのくらいある測定しましたか?
私たちは、テーブルの列を見ることができます:
| 失敗 | 失敗の確率 | 成功の確率 | |
|---|---|---|---|
| \(X ^ 1 \) | 0 | \(\ FRAC {1} {2 ^ {N-1}} \) | \(FRAC \ 1- {1} {2 ^ {N-1}} \) |
| \(X ^ 2 \) | 0、\(X ^ 1 \) | \(\ FRAC {2} {2 ^ {N-1}} \) | \(FRAC \ 1- {1} {2 ^ {N-2}} \) |
| \(X ^ 3 \) | 0、 \(X ^ 1 \) 、\(X ^ 2 \) 、\(X ^ 1 + X ^ 2 \) | \(\ FRAC {4} {2 ^ {N-1}} \) | \(FRAC \ 1- {1} {2 ^ {N-3}} \) |
| ...... | ...... | ............ | \(FRAC \ 1- {1} {2 ^ {N-1}} \) |
| \(X ^ {N-1} \) | 0、 \(X ^ 1 \) ...... \(X ^ 1 + X ^ 2 \) ...... \(X ^ 1 + X ^ 2 + ... + X ^ N-2 \) | \(\ FRAC {2 ^ {N-2}} {2 ^ {N-1}} \) | \(1- FRAC \ {1} {2} \) |
すべての措置は、次の3つの条件に分かれて失敗します。
- すべての0を測定
- 測定された結果は、上記と同じです
- 測定結果は、上記測定結果の線形結合であります
その成功の全体的な確率を計算するために、成功の確率に依存しないと考えられているここでは、成功の確率はの製品であるため、その
\(\ FRAC {1} {2} * \ FRAC {3} {4} * \ FRAC {7} {8} * ... * \ FRAC {2 ^ {N-1} -1} {2 ^ {N -1}} \)
この制限上記の問題の式Qシリーズを求めている、と興味を持って友人は0.28878とほぼ等しく、ここでは直接の確率が与えられ、解決する方法をルックアップするために行くことができます
注意:
このすべてがうまくなりますように私たちは考えていないですか?
いいえ、注意すべき場所は、私の友人の多くが知っていた、それを崩壊した量子状態を測定が終了していないのですか?なぜ、n-1の時間を測定することができますか?
実際には、これはあなたがn-1持つことができるように、N-1回を行うための最初の部分である(| X \ rangle \)\を線形測定条件xを見つけるためにあなたを満たすために。
参考文献: